Свойства трапеции, используемые при решении задач
Для выполнения контрольных работ.
для студентов по специальностям:
140211 – Электроснабжение;
140408 – Релейная защита и автоматизация электроэнергетических систем;
110301.65 – Механизация сельского хозяйства;
280302 – Инженерные системы сельскохозяйственного водоснабжения, обводнения и водоотведения.
Волгоград
ИПК «Нива»
УДК 51 (07)
ББК 22.1 я 7
М 54
Методические указания по дисциплине «Математика» для выполнения контрольных работ.
/Сост. А. А. Шубович; Волгогр. Гос. с.-х. акад. Волгоград, 2011. 24 с.
В данную часть справочника входит раздел планиметрии и стереометрии по геометрии. Надо знать, что решение задач по геометрии обладает определённой спецификой. В отличие от арифметики и алгебры любую задачу по геометрии необходимо смоделировать, т.е. построить чертёж, без которого решение невозможно. После этого в настоящее время общеприняты алгебраические способы решения задач по геометрии. При этом составляются уравнения или их системы, в которые входят неизвестные геометрические характеристики. Для этого нужно знать основные свойства простейших геометрических фигур на плоскости и тел в пространстве. Особенно важны формулы по геометрии, связывающие те или иные геометрические величины. Многие эти вопросы освещает данное пособие.
Для школьников, абитуриентов и студентов всех специальностей.
Рекомендовано методической комиссией факультета электрификации с.-х. Волгоградской ГСХА (протокол № 3 от 12 ноября 2010 г.)
УДК 51 (07)
ББК 22.1 я 7
© А.А. Шубович, 2011
© ФГОУ ВПО «Волгоградская государственная
сельскохозяйственная академия, 2011
Оглавление
От автора……………………………………………………………………..…2
Планиметрия……………………………………………………………………4
Параллельность и перпендикулярность прямых на плоскости……………………………..4
Треугольник………………………………………………………………………………….…5
Прямоугольный треугольник……………………………………………………………….…5
Соотношения в прямоугольном треугольнике……………………………………………….5
Равносторонний треугольник………………………………………………...……………….6
Равнобедренный треугольник…………………………………………………………………6
Произвольный треугольник……………………………………………………...……………6
Неравенство треугольника………………………………………………………………...…..6
Средняя линия треугольника………………………………………………………………….7
Сравнение треугольников……………………………………………………………….…….7
Признаки равенства треугольников…………………………………………………….…….7
Признаки равенства прямоугольных треугольников………………………………………..7
Подобные треугольники и признаки подобия треугольников……………………………...7
Формулы, связанные с площадью треугольника…………………………………………….8
Замечательные точки треугольника…………………………………………………………..8
Биссектриса треугольника…………………………………….....……………………………8
Медиана треугольника………………………………………………………………………...9
Высота треугольника…………………………………………………………………………10
Серединный перпендикуляр……………………………………………………………...….10
Вневписанная окружность……………………………………………………………...……11
Четырехугольник………………………………………………………………… …………12
Произвольный выпуклый четырёхугольник……………………………………………..…12
Квадрат, прямоугольник, параллелограмм ……………………………………..……..……12
Ромб, трапеция……………………………………………………………………..…………13
Описанный и вписанный четырехугольник……………………………………………...…14
Многоугольник………………………………………………………………………………..14
Выпуклый и правильный многоугольник…………………………………………………..14
Окружность, круг, сегмент и сектор………………………………………………..……….15
Свойства углов, хорд, секущих и касательной в окружности……………………………..15
Векторы на плоскости и в пространстве………………..………………………….……….16
Уравнение окружности……………………………………………………………………….19
Уравнение сферы……………………………………………………………………………..20
Стереометрия……………………………………………………………...…..20
Простейшие понятия стереометрии……………………………………………..………..…20
Наклонная, перпендикуляр, проекция……………….…………………………………...…20
Расстояние от точки до плоскости…………...…..…………………………………………20
Многогранники…………………………………...………..…………………………………21
Прямая и наклонная призма, параллелепипед ……………………………………………..21
Куб, пирамида ……………………………………………...………………………………...22
Усеченная пирамида………………………………………..…….…………………………..23
Цилиндр, конус, усеченный конус ……………………….…………………………………23
Шар и сфера………………………………………………………………….…………….….24
Шаровой сегмент……………………………………………………………..………………24
Шаровой сектор……………………………………………………………..………………..24
Шаровой слой……………………………………………………………….………………..24
Библиография…………………………………………………………………………………24
Планиметрия.
I. Параллельность и перпендикулярность прямых на плоскости.
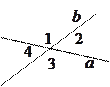
При пересечении двух прямых образуются пары углов:
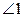 ,
, 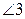 ;
; 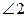 ,
, 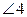 - вертикальные;
- вертикальные;
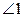 ,
, 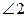 ;
; 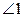 ,
, 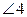 ;
; 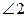 ,
, 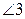 ;
; 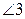 ,
, 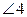 - смежные.
- смежные.
- Вертикальные углы равны.
2. Сумма смежных углов равна 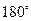 .
.
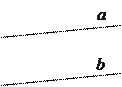
Две прямые на плоскости называются параллельными, если они не пересекаются.
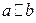 .
.
При пересечении двух прямых третьей прямой образуются следующие пары углов:
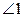 ,
, 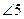 ;
; 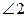 ,
, 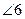 ;
; 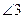 ,
, 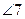 ;
; 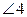 ,
, 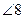 - соответственные;
- соответственные;
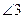 ,
, 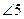 ;
; 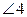 ,
, 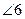 - внутренние накрест лежащие;
- внутренние накрест лежащие;
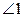 ,
, 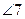 ;
; 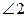 ,
, 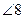 - внешние накрест лежащие;
- внешние накрест лежащие;
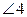 ,
, 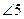 ;
; 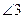 ,
, 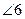 - внутренние односторонние;
- внутренние односторонние;
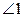 ,
, 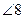 ;
; 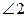 ,
, 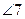 - внешние односторонние.
- внешние односторонние.
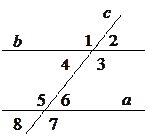 При пересечении двух параллельных прямых третьей:
При пересечении двух параллельных прямых третьей:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна
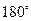 .
. - Сумма внешних односторонних углов равна
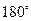 .
.
Признаки параллельности прямых:
1. Две прямые, параллельные третьей, параллельны.
2.  Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых третьей внутренние (или внешние) накрест лежащие углы равны, то прямые параллельны.
4. Если при пересечении двух прямых третьей сумма внутренних (или внешних) односторонних углов равна 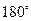 , то прямые параллельны.
, то прямые параллельны.
1. 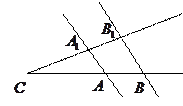 Теорема Фалеса: параллельные прямые, отсекающие на одной из пересекающихся прямых равные отрезки, отсекают на другой прямой также равные отрезки.
Теорема Фалеса: параллельные прямые, отсекающие на одной из пересекающихся прямых равные отрезки, отсекают на другой прямой также равные отрезки.
2. Параллельные прямые, пересекающие стороны угла, отсекают на них пропорциональные отрезки:
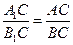 .
.
3. 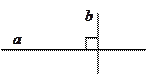 Прямые, отсекающие на сторонах угла пропорциональные отрезки, параллельны.
Прямые, отсекающие на сторонах угла пропорциональные отрезки, параллельны.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
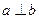 .
.
1. Две прямые, перпендикулярные третьей, параллельны.
2. Прямая, перпендикулярная одной из параллельных прямых, перпендикулярна и другой.
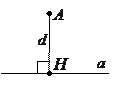 Расстоянием от точки до прямой является длина перпендикуляра, опущенного из точки на прямую:
Расстоянием от точки до прямой является длина перпендикуляра, опущенного из точки на прямую: 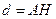 ,
, 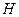 - основание перпендикуляра.
- основание перпендикуляра.
Если прямая задана уравнением, записанным в общем виде 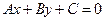 , то
, то
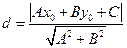 .
.
Расстоянием между параллельными прямыми является длина их общего перпендикуляра.
II. Треугольник.
1). Прямоугольный треугольник: 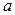 ,
, 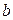 - катеты,
- катеты, 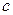 - гипотенуза.
- гипотенуза.
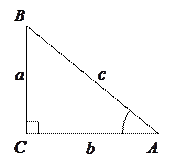 Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе: 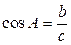 . Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе: 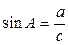 . Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему: 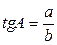 . Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему: 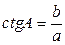 .
.
2). Соотношения в прямоугольном треугольнике: 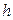 - высота, опущенная на гипотенузу,
- высота, опущенная на гипотенузу, 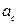 и
и 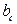 - проекции катетов на гипотенузу,
- проекции катетов на гипотенузу, 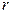 и
и 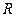 - радиусы вписанной и описанной окружности,
- радиусы вписанной и описанной окружности, 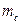 - медиана,
- медиана, 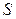 - площадь.
- площадь.
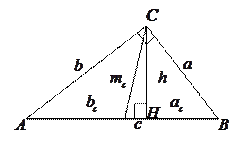
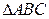 ;
; 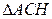 и
и 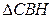 подобны.
подобны.
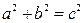 ;
; 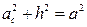 ;
; 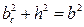 ;
;
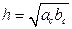 ;
; 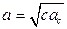 ;
; 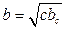 ;
; 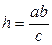 ;
;
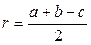 ;
; 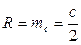 ;
; 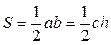 ;
;
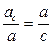 ;
; 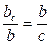 ;
; 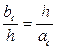 .
.
Признак прямоугольного треугольника: если в треугольнике квадрат одной из сторон равен сумме квадратов двух других, то треугольник является прямоугольным.
1. 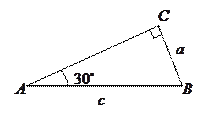 В прямоугольном треугольнике катет, лежащий против угла
В прямоугольном треугольнике катет, лежащий против угла 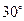 , равен половине гипотенузы:
, равен половине гипотенузы: 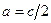 .
.
2. Если в треугольнике один из катетов равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 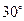 .
.
3). Равносторонний треугольник: 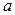 - сторона, тогда
- сторона, тогда
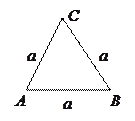
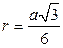 ;
; 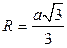 ;
;
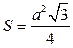 ;
; 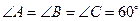 .
.
4). 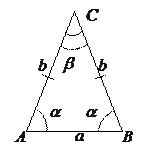 Равнобедренный треугольник:
Равнобедренный треугольник: 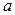 - основание,
- основание, 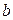 - боковая сторона,
- боковая сторона, 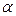 - угол при основании,
- угол при основании, 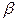 - угол при вершине,
- угол при вершине, 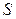 - площадь, тогда
- площадь, тогда
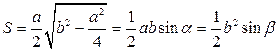 .
.
1. Углы при основании равнобедренного треугольника равны: 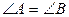 .
.
2. Признак равнобедренного треугольника: если два угла в треугольнике равны, то он является равнобедренным.
5). Произвольный треугольник: 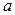 ,
, 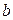 ,
, 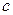 - стороны,
- стороны, 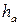 - высота,
- высота,
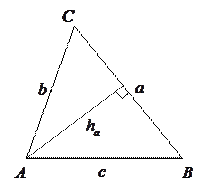
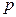 - полупериметр,
- полупериметр, 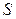 - площадь, тогда
- площадь, тогда
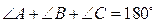 ,
,  ;
;
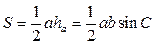 ;
;
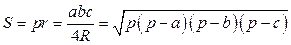 ;
;
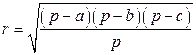 ;
;
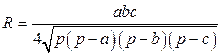 .
.
Теорема косинусов: 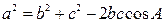 ;
; 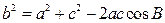 ;
; 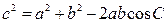 . Теорема синусов:
. Теорема синусов: 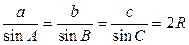 .
.
Неравенство треугольника: 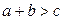 ;
; 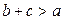 ;
; 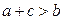 .
.
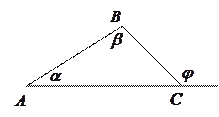 В любом треугольнике:
В любом треугольнике:
1. Против большей стороны лежит больший угол.
2. Против большего угла лежит большая сторона.
3. Против равных сторон лежат равные углы.
4. Против равных углов лежат равные стороны.
5. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним:
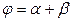 .
.
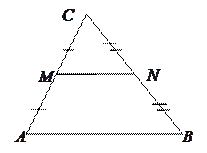 Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
1. Средняя линия треугольника параллельна противолежащей стороне: 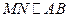 .
.
2. Средняя линия равна половине противолежащей стороны: 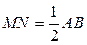 .
.
3. Отсекает от треугольника подобный ему треугольник, равный четверти площади исходного: 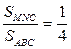 .
.
4. Отсекает на сторонах треугольника пропорциональные отрезки: 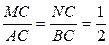 . Сравнение треугольников.
. Сравнение треугольников.
1). Признаки равенства треугольников.
1. По двум сторонам и углу между ними.
2. По стороне и прилежащим к ней углам.
3. По трём сторонам.
2). Признаки равенства прямоугольных треугольников.
1. По гипотенузе и катету.
2. По двум катетам.
3. По гипотенузе и острому углу.
4. По катету и прилежащему острому углу.
5. По катету и противолежащему острому углу.
3). 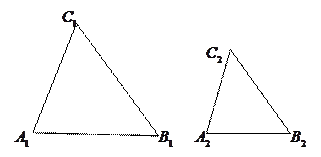 Подобные треугольники.
Подобные треугольники.
Два треугольника называются подобными, если стороны одного треугольника пропорциональны сторонам другого, а углы, образованные этими сторонами, равны, т.е. 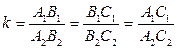 и
и 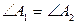 ,
, 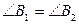 ,
, 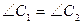 .
.
Число 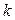 , равное отношению двух сходственных сторон, называется коэффициентом подобия.
, равное отношению двух сходственных сторон, называется коэффициентом подобия.
1. Отношение площадей подобных треугольников (фигур) равно квадрату коэффициента подобия: 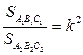 .
.
2. Отношение периметров подобных треугольников (фигур) равно коэффициенту подобия: 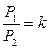 .
.
3. Если два треугольника подобны, то у них пропорциональны соответствующие биссектрисы, медианы, высоты и другие элементы.
4). Признаки подобия треугольников.
1. По двум углам.
2. По двум пропорциональным сторонам и углу между ними.
3. По трём пропорциональным сторонам.
5). Формулы, связанные с площадью треугольника.
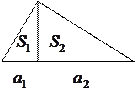
1. Если два треугольника имеют общую высоту, то их площади относятся как основания:
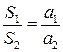 .
.
2. 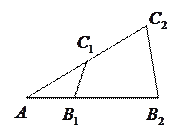 Если два треугольника имеют общий угол, то верно равенство:
Если два треугольника имеют общий угол, то верно равенство:
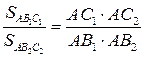 .
.
6). Замечательные точки треугольника.
К ним относятся: точка пересечения биссектрис, точка пересечения медиан, точка пересечения высот и точка пересечения серединных перпендикуляров произвольного треугольника. Все они совпадают только в правильном треугольнике.
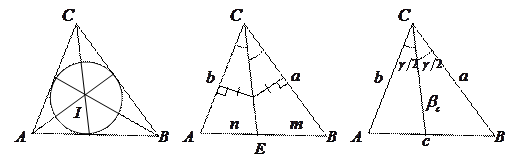
Биссектрисой угла называется луч, выходящий из вершины угла и делящий угол пополам.
Биссектрисой угла треугольника называется отрезок биссектрисы, соединяющий вершину с точкой на противолежащей стороне.
1. Каждая точка биссектрисы угла равноудалена от его сторон.
2. Биссектриса, проведённая к основанию равнобедренного треугольника, является медианой и высотой.
3. Биссектрисы треугольника пересекаются в одной точке ( 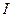 - инцентр).
- инцентр).
4. Инцентр является центром окружности, вписанной в треугольник.
5. Инцентр делит биссектрису угла 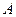 в отношении
в отношении 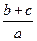 .
.
6. Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам:
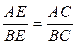 или
или 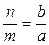 .
.
7. Биссектриса треугольника делит площадь в отношении, пропорциональном прилежащим сторонам: 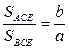 .
.
8. Для треугольника со сторонами 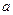 и
и 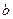 , между которыми угол
, между которыми угол 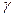 , длина биссектрисы
, длина биссектрисы 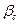 между этими сторонами:
между этими сторонами:
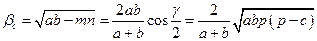 .
.
9. Выражение биссектрисы через длины сторон треугольника:
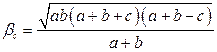 .
.
10. Теорема трилистника: если продолжение биссектрисы угла 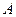 пересекает описанную окружность
пересекает описанную окружность 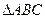 в точке
в точке 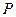 , то выполняется равенство:
, то выполняется равенство:
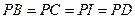 ,
,
где 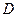 - центр вневписанной окружности, касающейся стороны
- центр вневписанной окружности, касающейся стороны 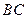 .
.
11. Формула Эйлера: расстояние между инцентром 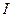 и центром описанной окружности
и центром описанной окружности 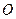 выражается формулой:
выражается формулой:
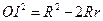 .
.
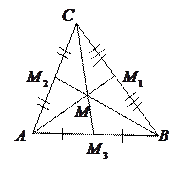 Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
1. Медиана делит треугольник на два равновеликих (одинаковой площади).
2. Медианы треугольника пересекаются в одной точке ( 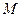 - центроид) и делятся в отношении
- центроид) и делятся в отношении 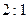 , считая от вершины:
, считая от вершины:
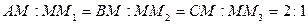 .
.
3. Медиана, проведённая к основанию равнобедренного треугольника, является биссектрисой и высотой.
4. Центроид лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и делит его в отношении 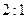 .
.
5. Если в вершины треугольника поместить равные массы, то центр масс будет совпадать с центроидом.
6. Центр масс треугольника с равномерно распределенной массой также находится в центроиде.
7. Если 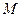 - центроид
- центроид 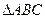 , то для любой точки
, то для любой точки 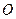 верно равенство:
верно равенство:
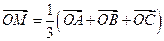 .
.
8. 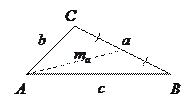 Теорема Лейбница: центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника имеет наименьшее значение.
Теорема Лейбница: центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника имеет наименьшее значение.
9. Для треугольника со сторонами 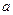 ,
, 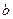 ,
, 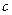 медиана, проведенная к стороне
медиана, проведенная к стороне 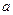 :
:
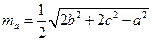 .
.
10. Сторона треугольника через три медианы:
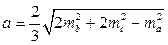 .
.
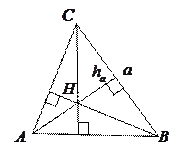 Высотой треугольника называется отрезок перпендикуляра, соединяющий вершину треугольника с точкой на противолежащей стороне.
Высотой треугольника называется отрезок перпендикуляра, соединяющий вершину треугольника с точкой на противолежащей стороне.
1. Высоты треугольника (или их продолжения) пересекаются в одной точке ( 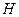 - ортоцентр).
- ортоцентр).
2. Ортоцентр находится внутри остроугольного треугольника, вне тупоугольного треугольника и в прямоугольном треугольнике совпадает с вершиной прямого угла.
3. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
4. Если в четверке точек 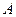 ,
, 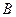 ,
, 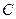 ,
, 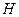 точка
точка 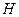 является точкой пересечения высот
является точкой пересечения высот 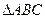 , то любая из четырех точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четверку называют ортоцентрической системой точек.
, то любая из четырех точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четверку называют ортоцентрической системой точек.
5. Радиусы окружностей, проходящих через любые три точки ортоцентрической системы равны.
6. Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек.
7. Ортоцентр остроугольного треугольника является центром треугольника, вписанной в его ортотреугольник.
8. Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
9. Точки, симметричные ортоцентру относительно его сторон, лежат на описанной окружности.
10. Точки, симметричные ортоцентру относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
11. Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
12. Если 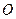 - центр описанной окружности
- центр описанной окружности 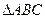 , то
, то
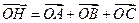 .
.
13. Для треугольника со сторонами 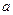 ,
, 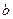 ,
, 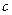 высота, проведенная к стороне
высота, проведенная к стороне 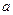 :
:
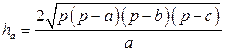 .
.
14. Зависимость между высотами треугольника и радиусом 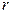 вписанной окружности:
вписанной окружности:
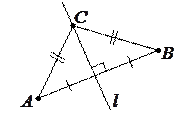
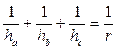 .
.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему.
1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
2. Каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
3. 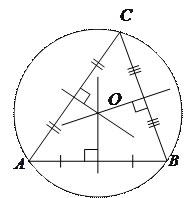 Точка пересечения серединных перпендикуляров является центром окружности, описанной около треугольника.
Точка пересечения серединных перпендикуляров является центром окружности, описанной около треугольника.
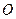 - центр описанной окружности.
- центр описанной окружности.
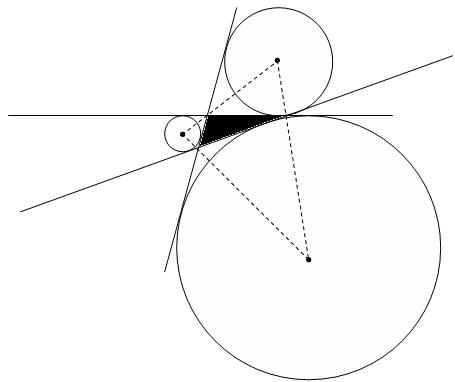
Вневписанная окружностьтреугольника – окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон.
1. Существование и единственность вневписанной окружности обусловлено тем, что биссектрисы двух внешних углов треугольника и биссектриса внутреннего угла, не смежного с данными двумя, пересекаются в одной точке, которая является центром такой окружности.
2. Таких окружностей для любого треугольника существует ровно 3.
3. Длина отрезка касательной, проведенной к вневписанной окружности равна полупериметру треугольника.
4. Исходный треугольник является ортотреугольником 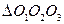 .
.
Дан 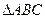 со сторонами
со сторонами 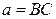 ,
, 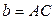 ,
, 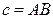 ,
, 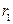 ,
, 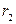 ,
, 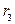 - радиусы вневписанных окружностей, касающиеся соответственно сторон
- радиусы вневписанных окружностей, касающиеся соответственно сторон 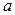 ,
, 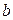 ,
, 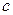 треугольника;
треугольника; 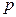 - полупериметр;
- полупериметр; 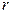 ,
, 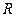 - радиусы вписанной и описанной окружности,
- радиусы вписанной и описанной окружности, 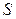 - площадь.
- площадь.
5. Формула Эйлера: 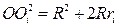 , где
, где 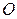 - центр описанной окружности.
- центр описанной окружности.
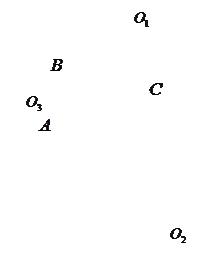
6. Радиусы: 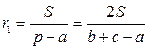 ;
; 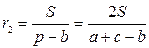 ;
; 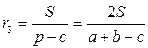 .
.
7. Площадь: 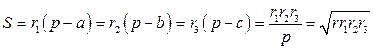 .
.
8. Соотношения между радиусами: 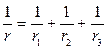 ;
; 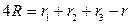 ;
;
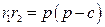 ;
; 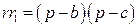 .
.
III. Четырехугольник.
1). Произвольный выпуклый четырёхугольник:
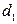 ,
, 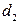 - диагонали,
- диагонали, 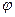 - угол между ними, тогда
- угол между ними, тогда
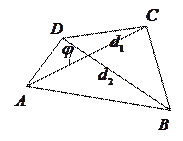 |
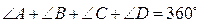 ;
;
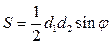 .
.
Свойство: центроид произвольного четырехугольника лежит в точке пересечения средних линий четырехугольника и делит их пополам.
2). Квадрат: 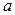 - сторона,
- сторона, 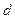 - диагональ, тогда
- диагональ, тогда
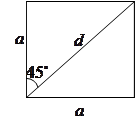
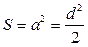 ;
; 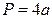 ;
; 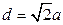 ;
;
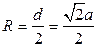 ;
; 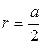 .
.
3). Прямоугольник: 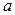 ,
, 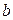 - стороны,
- стороны, 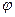 - угол между диагоналями, тогда
- угол между диагоналями, тогда
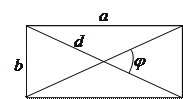
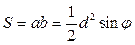 ;
; 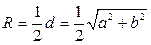 ;
; 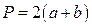 .
.
Признак прямоугольника: если в параллелограмме диагонали равны, то он является прямоугольником.
4). 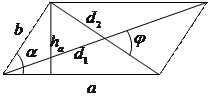 Параллелограмм:
Параллелограмм: 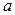 ,
, 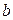 - стороны,
- стороны, 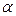 - угол между ними,
- угол между ними,
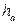 - высота, проведённая к стороне
- высота, проведённая к стороне 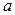 , тогда
, тогда
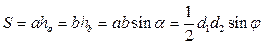 ;
;
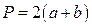 ;
; 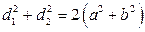 .
.
Признаки параллелограмма:
1. Если в четырёхугольнике две противоположные стороны параллельны и равны, то он является параллелограммом.
2. Если в четырёхугольнике противоположные стороны попарно параллельны, то он является параллелограммом.
3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то он является параллелограммом.
5). Ромб: 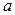 - сторона,
- сторона, 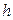 - высота,
- высота, 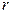 - радиус вписанной окружности, тогда
- радиус вписанной окружности, тогда
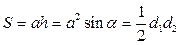
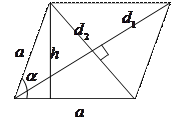 ;
; 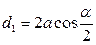 ;
; 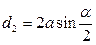 ;
; 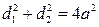 ;
; 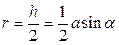 ;
; 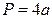 .
.
6). 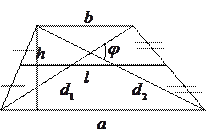 Трапеция:
Трапеция: 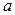 ,
, 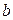 - основания,
- основания, 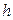 - высота,
- высота, 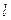 - средняя линия, тогда
- средняя линия, тогда
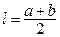 ;
;
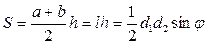 .
.
Свойства трапеции, используемые при решении задач.
1. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной. Площади треугольников, прилежащих к боковым сторонам, равны.
2. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которых лежат боковые стороны, лежат на одной прямой.
3. В равнобокой трапеции углы при основании равны.
4. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции.
5. В равнобокой трапеции диагонали равны.
6. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме.
7. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой.
8. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.
9. Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.
10. Во всякой трапеции с основаниями 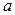 и
и 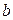 отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен
отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен 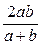 (есть среднее гармоническое оснований).
(есть среднее гармоническое оснований).
11. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
12. Трапецию можно описать около окружности тогда и только когда, когда сумма оснований равна сумме боковых сторон.
13. Окружность, вписанная в равнобокую трапецию, касается оснований в их серединах.
14. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему геометрическому её оснований.
7). Описанный четырёхугольник:

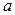 ,
, 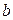 ,
, 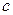 ,
, 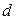 - стороны, тогда
- стороны, тогда
суммы противоположных сторон равны:
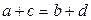 ;
;
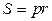 , где
, где 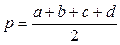 - полупериметр.
- полупериметр.
8). 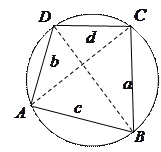 Вписанный четырёхугольник:
Вписанный четырёхугольник:
суммы противоположных углов равны:
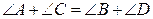 ;
;
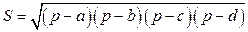 .
.
Теорема Птоломея: в выпуклом четырехугольнике, вписанном в круг, произведение диагоналей равно сумме произведений противоположных сторон:
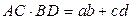 .
.
IV. Многоугольник.
1) Выпуклый n – угольник.
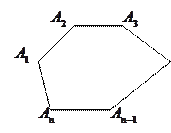
Сумма углов равна 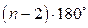 (не обязательно выпуклого).
(не обязательно выпуклого).
Число диагоналей 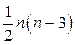 .
.
2) Правильный многоугольник:
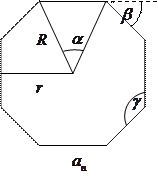
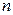 - число сторон,
- число сторон, 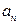 -сторона,
-сторона, 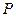 - периметр,
- периметр,
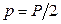 - полупериметр,
- полупериметр,
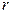 и
и 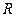 - радиус вписанной и описанной окружности;
- радиус вписанной и описанной окружности;
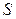 - площадь,
- площадь, 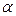 - центральный угол,
- центральный угол,
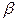 - внешний угол,
- внешний угол, 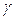 - внутренний угол, тогда
- внутренний угол, тогда
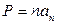 ;
; 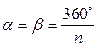 ;
; 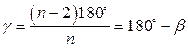 ;
; 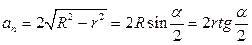 ;
;
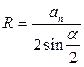 ;
; 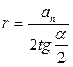 ;
; 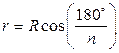 ;
;
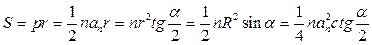 .
.
V. Окружность и круг.
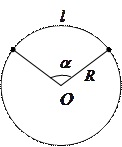
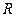 - радиус,
- радиус, 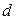 - диаметр,
- диаметр, 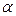 - центральный угол в градусах,
- центральный угол в градусах, 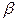 - в радианах,
- в радианах, 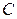 - длина окружности,
- длина окружности, 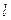 - длина дуги окружности, соответствующая центральному углу,
- длина дуги окружности, соответствующая центральному углу, 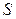 - площадь круга, тогда
- площадь круга, тогда
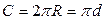 ;
; 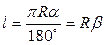 ;
; 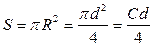 .
.
VI. Сегмент и сектор: 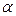 - центральный угол в градусах,
- центральный угол в градусах, 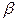 - в радианах,
- в радианах, 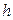 - высота сегмента, тогда
- высота сегмента, тогда
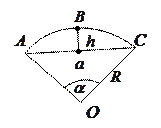
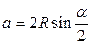 ;
; 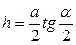 .
.
Площадь сектора: 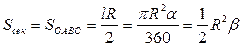 .
.
Площадь сегмента: 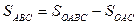 .
.
VII. Свойства углов, хорд, секущих и касательной в окружности.
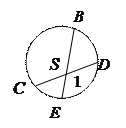
 1). Произведения отрезков
1). Произведения отрезков
пересекающихся хорд равны:
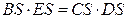 .
.
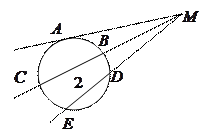
2). Квадрат касательной равен произведению секущей на её внешнюю часть:
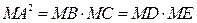 .
.
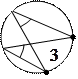
 3). Углы, вписанные в окружность,
3). Углы, вписанные в окружность,
опирающиеся на одну и ту же дугу, равны.
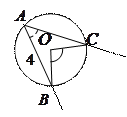
4). Угол, вписанный в окружность, если он острый, равен половине дуги, на которую он опирается:
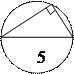

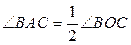 ;
;
и если тупой, то 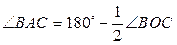 .
.
5). Вписанный угол, опирающийся на диаметр, - прямой.
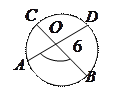
6). Угол между двумя хордами равен полусумме
дуг, заключённых между его сторонами: 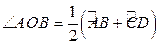 .
.
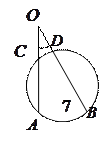 7). Угол между двумя секущими равен полуразности дуг,
7). Угол между двумя секущими равен полуразности дуг, 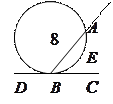 заключённых между его сторонами:
заключённых между его сторонами: 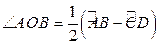 .
.
8). Угол между касательной и хордой измеряется половиной дуги, заключённой внутри него:
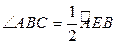 .
.
9). Угол между касательной и секущей равен 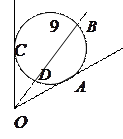 полуразности дуг, заключённых между его сторонами:
полуразности дуг, заключённых между его сторонами:
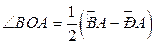 . Описанный угол равен полуразности дуг, заключённых между его сторонами:
. Описанный угол равен полуразности дуг, заключённых между его сторонами: 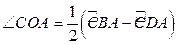 .
.
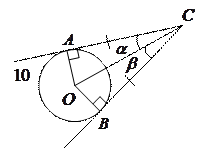 10). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания:
10). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания: 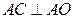 .
.
Отрезки касательных к окружности, проведенные из одной точки к окружности, равны: 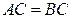 и составляют равные углы с прямой, проходящей через эту точку и центр окружности:
и составляют равные углы с прямой, проходящей через эту точку и центр окружности: 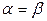 .
.
