Критерий устойчивости Рауса-Гурвица

Критерий Рауса-Гурвица используется при анализе устойчивости линейных стационарных систем. Он позволяет аналитически определить, все ли корни полинома имеют отрицательные действительные части.

Вещественные части корней будут отрицательными в том случае, если все коэффициенты уравнения и диагональные миноры главного определителя будут положительными. Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с a₁в возрастающем порядке до a_n. От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз - с убывающими индексами. Места в матрице коэффициентов с индексами больше n и меньше 0 заполняются нулями.

Критерий Гурвица формируется следующим образом:

для того, что бы АСУ была устойчива, необходимо и достаточно, что бы все определители Гурвица (∆₁, ∆₂, …, ∆_n) были положительными, и при этом выполнялось условие а₀>0.

Рассмотрим выражение критерия Гурвица для характеристического уравнения третьего порядка

a₀s³+ a₁s²+a₂s+a₃ = 0

Главный определитель

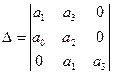
Условие Гурвица

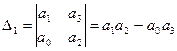> 0

Следовательно, система будет устойчивой, если все коэффициенты a₀,a₁,a₂,a₃ положительны и a₁a₂ −a₀a₃ > 0, и a₀ > 0.

Критерий устойчивости Михайлова

В основу критерия Михайлова положен принцип аргумента: произведение комплексных чисел имеет аргумент, равный сумме аргументов всех его сомножителей.

Чтобы все корни характеристического уравнения

a₀sⁿ + a₁sⁿ⁻¹+...+ a_n−1s + a_n = 0

имели отрицательные вещественные части, необходимо, чтобы после подстановки частоты в соответствующий характеристический полином D(s) полное приращение его фазы при изменении частоты ω от нуля до бесконечности составляло nπ/2, где n – степень полинома D(s). При этом характеристический полином опишет в комплексной плоскости кривую – «годограф Михайлова».

Свойства годографа Михайлова:

1) годограф всегда спиралевиден;

2) при ω = 0, годограф начинается с точки на вещественной оси;

3) годограф уходит в бесконечность при ω → ∞;

4) при четном n, годограф стремится к бесконечности параллельно вещественной оси; при n - нечетном, годограф стремится к ∞ параллельно мнимой оси.

Замкнутая система устойчива в том случае, если годограф Михайлова при изменении ω от 0 до ∞ проходит в положительном направлении n квадрантов комплекса плоскости, начиная свое движение от положительной вещественной полуоси, и при этом нигде не обращается в нуль.

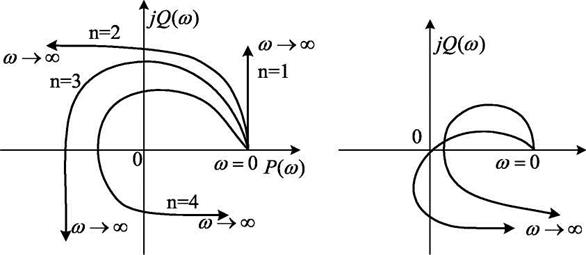
Рисунок 2 – Годограф Михайлова: а) для устойчивых систем; б) для неустойчивых систем.