Критерий устойчивости Рауса-Гурвица.

Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. В разной форме этот критерий был предложен английским математиком Е. Раусом и затем швейцарским математиком А. Гурвицем в конце 19 – го века. Приведем без доказательства этот критерий в форме Гурвица.

Возьмем характеристический полином

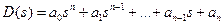, (7.8)

где полагаем 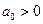, что всегда можно обеспечить умножением при необходимости полинома на - 1. Составим из коэффициентов этого полинома определитель

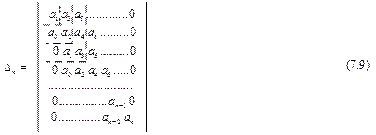
Этот определитель называется определителем Гурвица. Он имеет n строк и n столбцов. Первая строка содержит все нечетные коэффициенты до последнего, после чего строка заполняется до положительного числа n элементов нулями. Вторая строка включает все четные коэффициенты и тоже заканчивается нулями. Третья строка получается из первой, а четвертая – из второй сдвигом вправо на один элемент. На освободившееся при этом слева место ставится нуль. Аналогично сдвигом вправо на элемент получаются все последующие нечетные и четные строки из предыдущих одноименных строк.

В результате в главной диагонали определителя оказываются последовательно все коэффициенты, кроме а₀.

Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.

Эти миноры отчерчены в выражении (7.9) штриховыми линиями.

Развернем критерий Гурвица для нескольких конкретных значений n.

Для n = 1

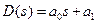
И условия устойчивости сводятся к неравенствам:

.

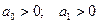Отсюда, например, звено 1-го порядка с передаточной функцией 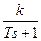является устойчивым, а звено с передаточной функцией 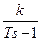- неустойчивым.

Для n = 2

;

.

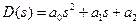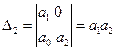Условия устойчивости:

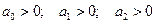
(к последнему неравенству сводится неравенство 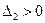, если учесть предыдущее неравенство ).

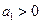Например, звено с передаточной функцией 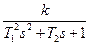устойчиво, если перед всеми членами в знаменателе стоит знак плюс.

Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов a_i.

Если определитель D_n=0, то система находится на границе устойчивости. Возможны два случая:

§ апериодическая граница устойчивости, если свободный член характеристического уравнения равен нулю, что соответствует нейтрально устойчивой системе;

§ колебательная граница устойчивости, если определитель D_n-1=0.

Из условия D_n-1=0 можно определить параметры, при которых система находится на границе устойчивости.

Для n = 3

;

.

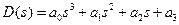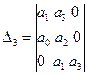Условия устойчивости:

;

;

.

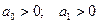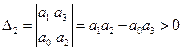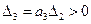Последнее неравенство с учетом предпоследнего условия 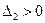сводится к требованию 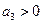. Таким образом, в целом эти условия устойчивости заключаются в положительности всех коэффициентов и предпоследнего минора Δ₂. (Необходимость положительности а₂ вытекает из условия 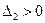и положительности всех остальных коэффициентов).

Для n = 4

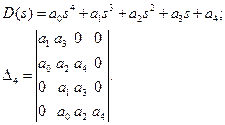
Условия устойчивости:

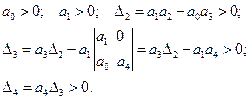
Легко видеть, что условия устойчивости опять сводятся к требованию положительности всех коэффициентов и предпоследнего минора Δ₃. (Условие Δ₂ > 0 при этом вытекает из неравенства Δ₃ > 0 с учетом того, что а₄ > 0).

Для n = 5

.

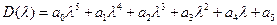Условия устойчивости, если действовать аналогично, сведутся здесь к положительности всех коэффициентов и двух миноров: Δ₂ и предпоследнего Δ₄.

Можно показать в общем случае для системы n – го порядка, что в условия устойчивости в качестве их части входит требование положительности всех коэффициентов уравнения. Анализ устойчивости надо начинать с проверки этого простого необходимого, но недостаточного условия устойчивости. При его невыполнении, естественно, отпадает надобность в составлении и проверке остальных неравенств.

Условия устойчивости, получаемые из критерия Рауса-Гурвица, как видно из изложенного, усложняются с ростом порядка системы. При этом для систем достаточно высокого порядка оказывается затруднительным выяснять влияние на устойчивость системы значений отдельных параметров звеньев, входящих в состав коэффициентов уравнения. Это связано с тем, что, как правило, одни и те же параметры одновременно входят в несколько коэффициентов уравнения системы. Поэтому критерий Рауса-Гурвица применяют только для систем невысокого порядка и прежде всего для анализа устойчивости, когда надо определить, устойчива ли система при известных значениях всех ее параметров. При решении задачи синтеза системы, когда требуется выбрать значения отдельных параметров системы, критерий Рауса-Гурвица становится неудобным уже для систем выше четвертого порядка.