Производная сложной функции. Рассмотренные нами правила дифференцирования результатов арифметических действий не дают еще возможности вычислять производные от многих элементарных функций
Рассмотренные нами правила дифференцирования результатов арифметических действий не дают еще возможности вычислять производные от многих элементарных функций. Возьмем, например, функцию 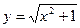 , которая не является ни суммой, ни произведением, ни частным более простых элементарных функций, и поэтому правила предыдущего параграфа к ней неприменимы. При этом
, которая не является ни суммой, ни произведением, ни частным более простых элементарных функций, и поэтому правила предыдущего параграфа к ней неприменимы. При этом 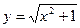 является сложной функцией:
является сложной функцией: 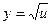 ,
, 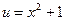 , и ее производную можно найти с помощью правила дифференцирования сложной функции, которое читается так.
, и ее производную можно найти с помощью правила дифференцирования сложной функции, которое читается так.
Если функция 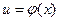 имеет производную в точке x, а функция
имеет производную в точке x, а функция 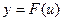 имеет производную в точке
имеет производную в точке 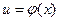 , то сложная функция
, то сложная функция 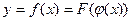 также имеет производную в точке x, причем
также имеет производную в точке x, причем 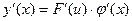 .
.
Опуская аргумент и используя другое обозначение для производных, формулу можно переписать в виде 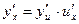 .
.
Доказательство:
Придадим x приращение ∆x, оно вызовет приращение ∆u промежуточного аргумента u=φ(x),
которое в свою очередь повлечет изменение функции y на некоторую величину ∆y.
Для отыскания производной y′ нужно найти 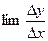 при∆x→0.
при∆x→0.
Представим отношение 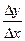 в виде
в виде
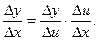
Тогда в силу правила предельного перехода в произведении получим:
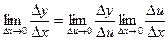
( ∆u→0 при ∆x→0, так как u=φ(x)- непрерывная функция).
Так как 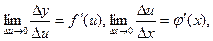
то мы приходим к доказанной формуле.
