Метод областей 4 страница
Графиком функции 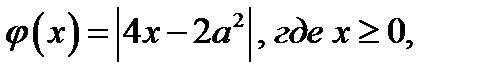 является «подвижный уголок» с вершиной в точке
является «подвижный уголок» с вершиной в точке 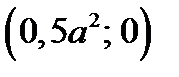 и со сторонами
и со сторонами
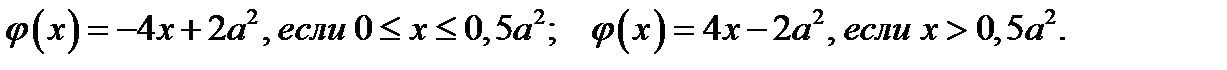
График функции 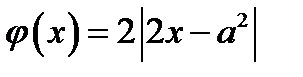 , где
, где 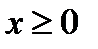 , отобразим относительно оси у и получим график функции
, отобразим относительно оси у и получим график функции 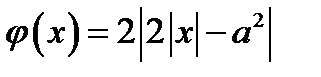 .
.
2. Функция 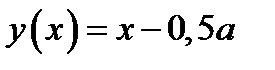 , где
, где 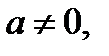 задаёт семейство параллельных прямых с угловым коэффициентом
задаёт семейство параллельных прямых с угловым коэффициентом 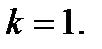
На рисунке 20 изображён график функции 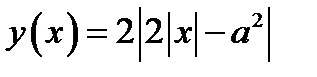 при
при
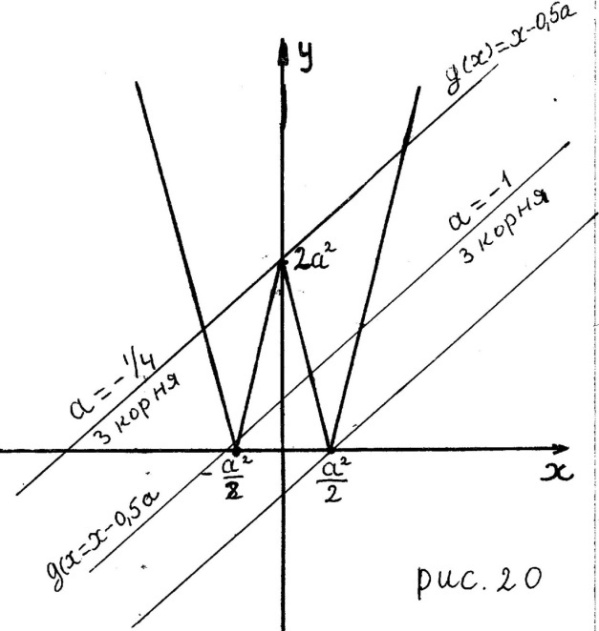 некотором значении параметра а, а также несколько прямых семейства функции
некотором значении параметра а, а также несколько прямых семейства функции 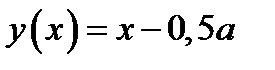 .
.
3. Исходное уравнение имеет три корня тогда и только тогда, когда прямая 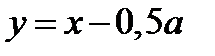 , где
, где 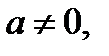 пересекает график функции
пересекает график функции 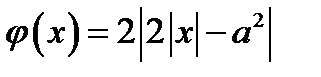 в трёх точках. Из рисунка 20 следует, что это возможно, если прямая
в трёх точках. Из рисунка 20 следует, что это возможно, если прямая 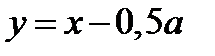 , где
, где 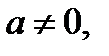 проходит через точку
проходит через точку 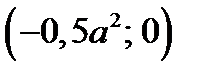 или через точку
или через точку 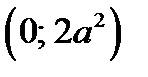 .
.
а) Прямая 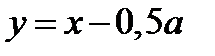 , где
, где 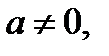 проходит через точку
проходит через точку 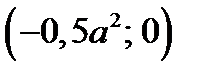 , если
, если 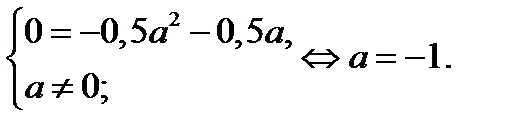
При 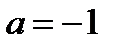 исходное уравнение принимает вид
исходное уравнение принимает вид 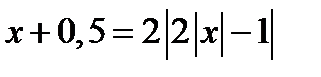 . Это уравнение имеет три корня.
. Это уравнение имеет три корня.
Из рисунка 20 следует, что один корень – это 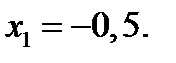 Два других корня являются корнями уравнения
Два других корня являются корнями уравнения 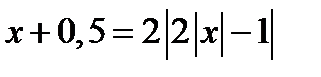 при
при 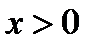 . Найдём эти корни. Имеем
. Найдём эти корни. Имеем
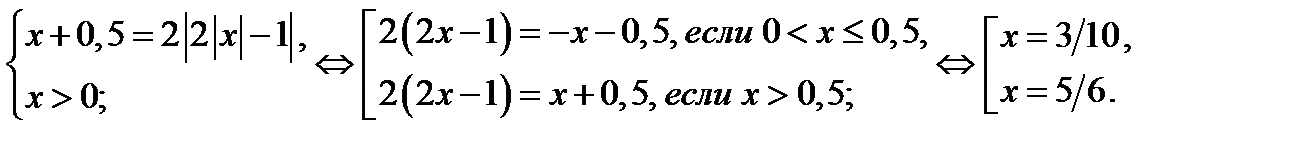
Итак, если 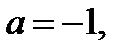 то исходное уравнение имеет три корня:
то исходное уравнение имеет три корня: 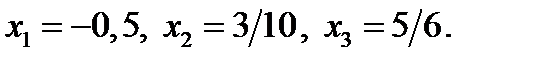
б) Прямая 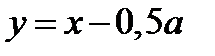 , где
, где 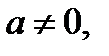 проходит через точку
проходит через точку 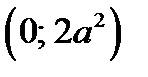 , если
, если 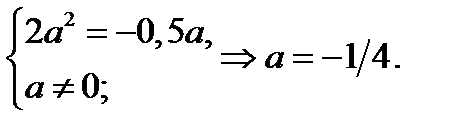
Итак, если 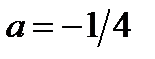 , то исходное уравнение принимает вид
, то исходное уравнение принимает вид 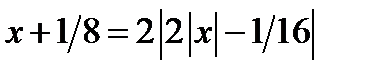 . Это уравнение имеет три корня.
. Это уравнение имеет три корня.
Найдём эти корни из уравнения
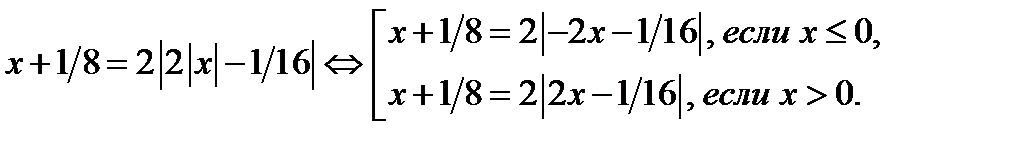 (17.1)
(17.1)
Первое уравнение совокупности (17.1) равносильно совокупности
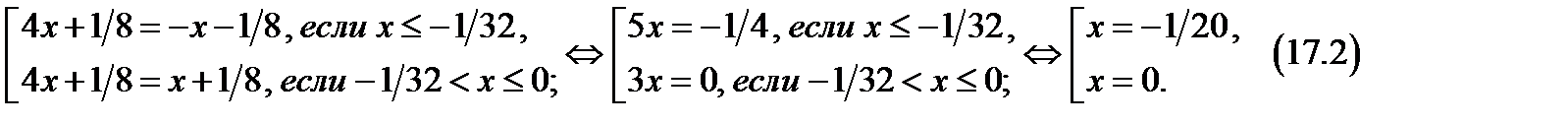
Из (17.2) следует: корнями первого уравнения совокупности (17.1), значит и исходного уравнении при 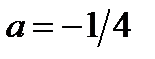 являются
являются 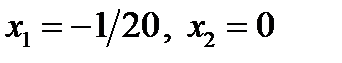 .
.
Второе уравнение совокупности (17.1) равносильно совокупности
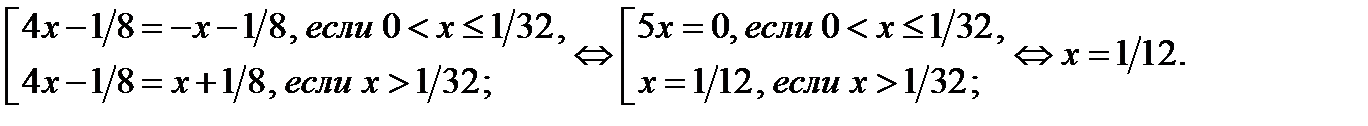
Корнем второго уравнения совокупности (17.1) является 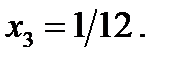
Итак, если 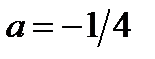 ,то исходное уравнение имеет три корня:
,то исходное уравнение имеет три корня: 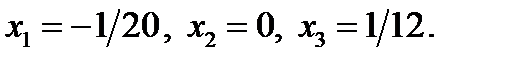
Ответ. Если 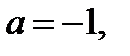 то
то 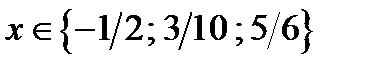 ; если
; если 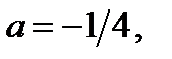 то
то 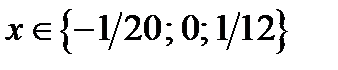 .
.
18. Найдите все значения параметра а, при которых уравнение 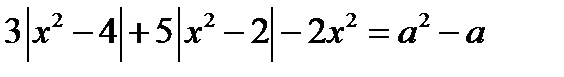 имеет бесконечное множество решений. Найдите множество решений уравнения при этих значениях параметра а.
имеет бесконечное множество решений. Найдите множество решений уравнения при этих значениях параметра а.
Решение. Сделаем замену 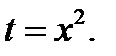 Очевидно,
Очевидно, 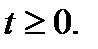
Исходное уравнение принимает вид
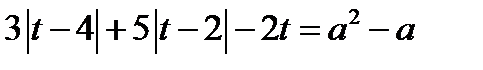 , где
, где 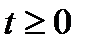 (18.1)
(18.1)
Отметим: исходное уравнение и уравнение (18.1) при одних и тех же значениях параметра а имеют бесконечное множество решений.
Уравнение (18.1) равносильно совокупности
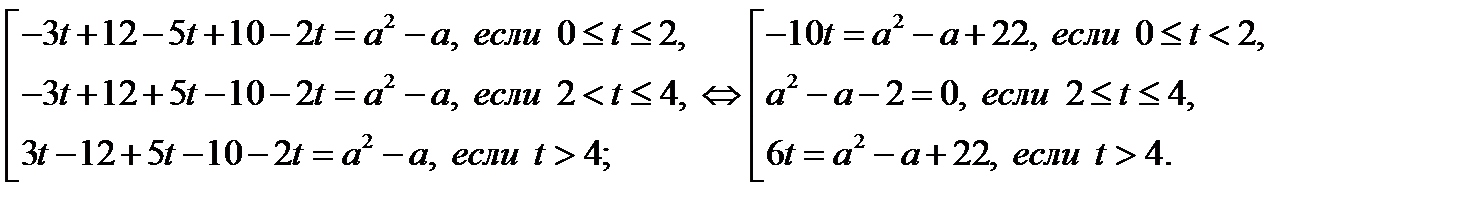
 Из последней совокупности следует, что уравнение (18.1) имеет бесконечное множество решений, если
Из последней совокупности следует, что уравнение (18.1) имеет бесконечное множество решений, если 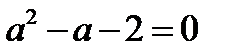 . (Отметим, что первое и третье уравнения последней совокупности имеют не более чем по одному решению.)
. (Отметим, что первое и третье уравнения последней совокупности имеют не более чем по одному решению.)
Так как корни уравнения 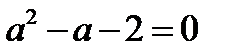 – это
– это 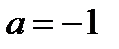 или
или 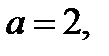 то при
то при 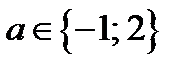 решениями уравнения (18.1) являются
решениями уравнения (18.1) являются 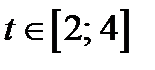 .
.
Так как 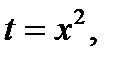 то при
то при 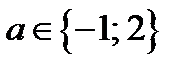 решениями исходного уравнения
решениями исходного уравнения
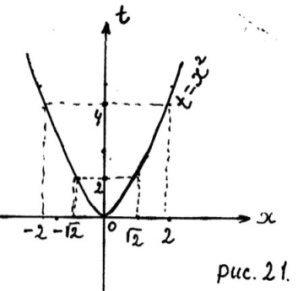
являются 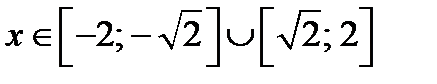 (рис 21, так как, если
(рис 21, так как, если 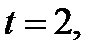 то
то 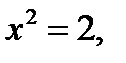 если
если 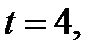 то
то 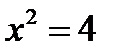 ).
).
Ответ. 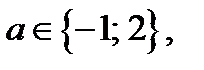
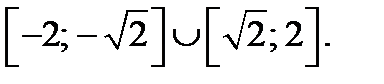
19. Решите уравнение 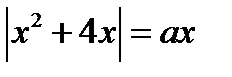 .
.
Решение. 1. Очевидно, что 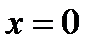 является корнем исходного уравнения при любом
является корнем исходного уравнения при любом 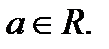
2. На плоскости 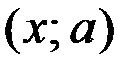 построим множество точек, удовлетворяющих исходному уравнению при условии, что
построим множество точек, удовлетворяющих исходному уравнению при условии, что 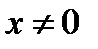 . Имеем
. Имеем
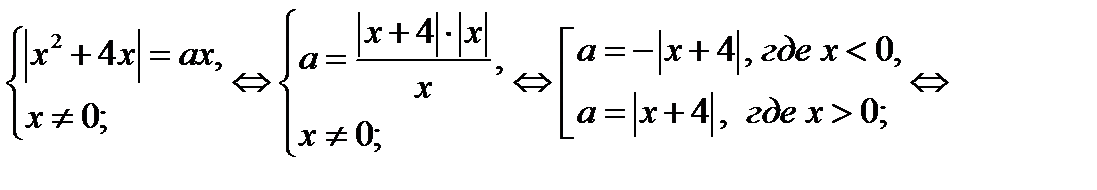
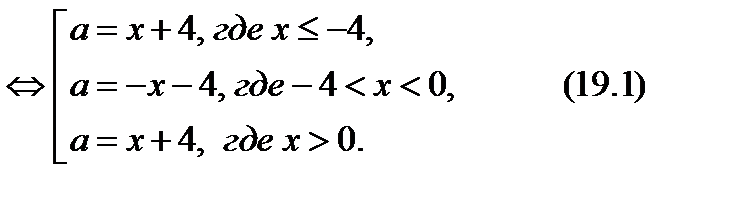
При 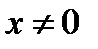 исходное уравнение равносильно совокупности (19.1).
исходное уравнение равносильно совокупности (19.1).
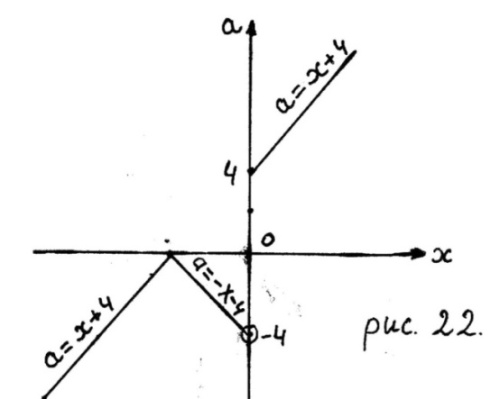 3. На рисунке 22 изображён график совокупности (19.1). Из рисунка 22 и так как
3. На рисунке 22 изображён график совокупности (19.1). Из рисунка 22 и так как 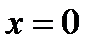 является корнем исходного уравнения при любом
является корнем исходного уравнения при любом 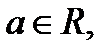 следует, что исходное уравнение имеет
следует, что исходное уравнение имеет
один корень 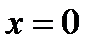 , если
, если 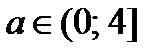 ; два корня:
; два корня: 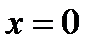 ,
, 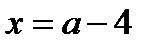 (корень
(корень 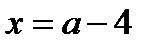 находим из уравнений 2 и 3 совокупности (19.1)), если
находим из уравнений 2 и 3 совокупности (19.1)), если 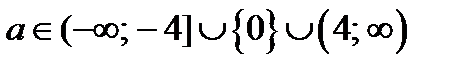 ; то три корня:
; то три корня: 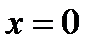 ,
, 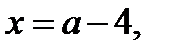
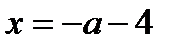 (последние два корня находим из уравнений 1 и 2 совокупности (19.1)), если
(последние два корня находим из уравнений 1 и 2 совокупности (19.1)), если 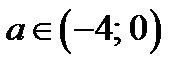 .
.
Ответ. Один корень 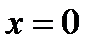 , если
, если 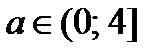 ; два корня:
; два корня: 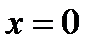 ,
, 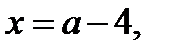 если
если 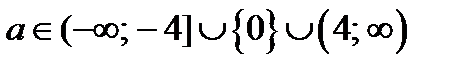 ; три корня:
; три корня: 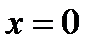 ,
, 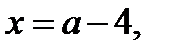
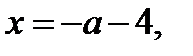 если
если 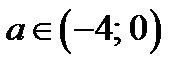 .
.
20.Найдите все значения параметра а, при каждом из которых уравнение 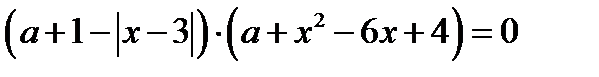 имеет 1) три корня; 2) два корня. Найдите эти корни.
имеет 1) три корня; 2) два корня. Найдите эти корни.
Решение. 1. Так как 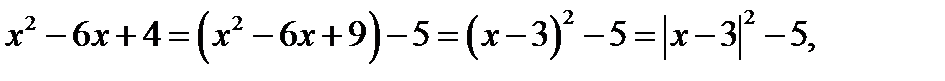
то исходное уравнение равносильно уравнению
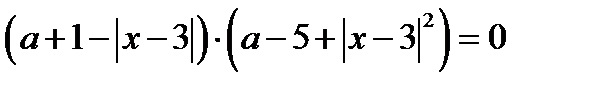
Сделаем замену 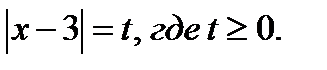
2. Рассмотрим уравнение 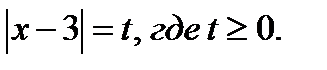 (20.1)
(20.1)
Если 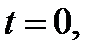 то уравнение (20.1) имеет единственный корень
то уравнение (20.1) имеет единственный корень 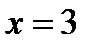 . Для любого
. Для любого 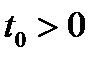 , уравнение (20.1) имеет два различных корня
, уравнение (20.1) имеет два различных корня 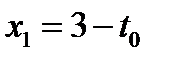 или
или 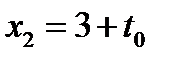 .
.
3. Если 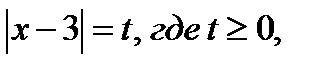 то исходное уравнение принимает вид
то исходное уравнение принимает вид
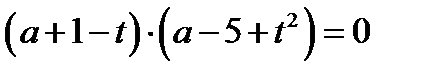 , где
, где 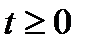 . (20.2)
. (20.2)
Уравнение (20.2) равносильно совокупности
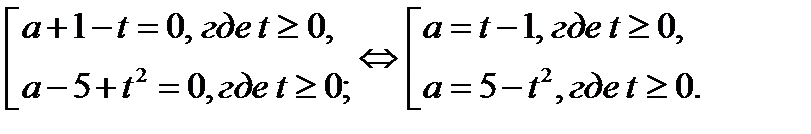
4. На плоскости 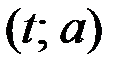 построим множество точек, удовлетворяющих последней совокупности.
построим множество точек, удовлетворяющих последней совокупности.
а) Графиком функции 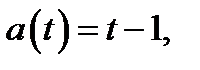 где
где 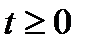 , является часть прямой. Из уравнения
, является часть прямой. Из уравнения 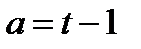 следует, что
следует, что 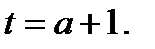 Обозначим
Обозначим 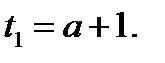
 б) Графиком функции
б) Графиком функции 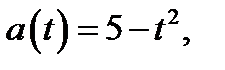 где
где 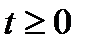 , является часть параболы. Из уравнения
, является часть параболы. Из уравнения 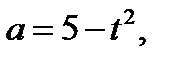 где
где 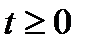 , следует, что
, следует, что 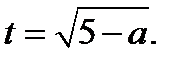 Обозначим
Обозначим 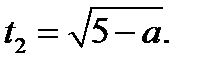
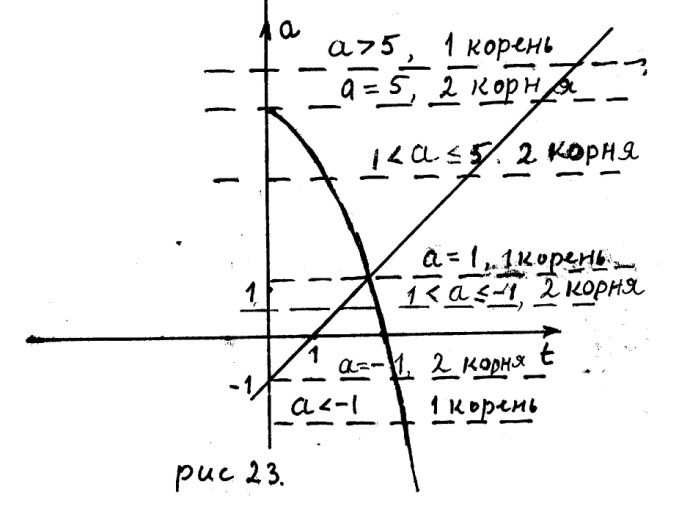
График рассматриваемой совокупности изображён на рисунке 23.
5. Исходное уравнение может иметь три корня только в случае, когда уравнение (20.2) имеет два корня, причём одним из корней является 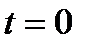 , а второй корень
, а второй корень 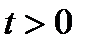 (следует из 2.).
(следует из 2.).
Из рисунка 23 следует, что уравнение (20.2) имеет два корня, причём одним из корней является 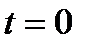 , в двух случаях.
, в двух случаях.
1) Если 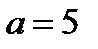 , то уравнение (20.2) имеет два корня:
, то уравнение (20.2) имеет два корня: 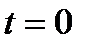 ,
, 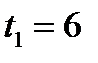 (так как
(так как 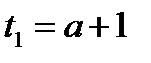 ). Так как
). Так как 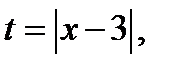 то из 2. следует, что при
то из 2. следует, что при 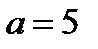 исходное уравнение имеет три различных корня:
исходное уравнение имеет три различных корня:
если 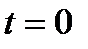 , то
, то 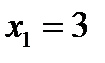 ;
;
если 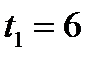 , то
, то 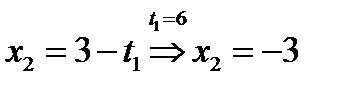 ,
, 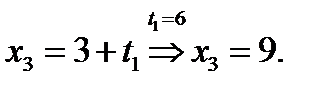
2) Если 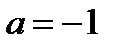 , то уравнение (20.2) имеет два корня:
, то уравнение (20.2) имеет два корня: 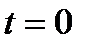 ,
, 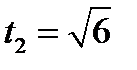 (так как
(так как 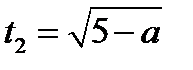 ). Так как
). Так как 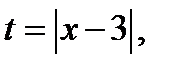 то из 2. следует, что при
то из 2. следует, что при 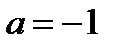 исходное уравнение имеет три различных корня:
исходное уравнение имеет три различных корня:
если 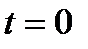 , то
, то 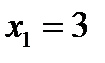 ;
;
если 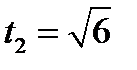 , то
, то 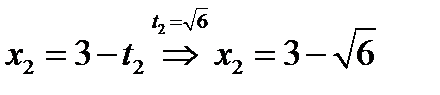 ,
, 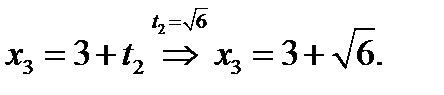
6. Исходное уравнение может иметь два корня только в случае, когда уравнение (20.2) имеет один корень, который не равен нулю.
Из рисунка 23 следует, что уравнение (20.2) имеет один корень в трёх случаях.
1) Если 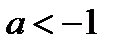 , то
, то 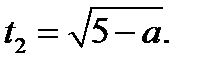
Из 2. следует, что при 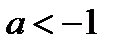 исходное уравнение имеет два корня:
исходное уравнение имеет два корня:
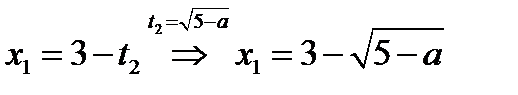 ,
, 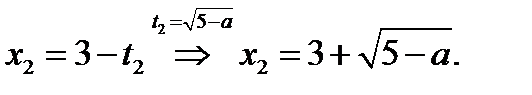
2) Если 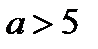 , то
, то 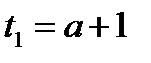 . Из 2. следует, что при
. Из 2. следует, что при 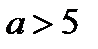 исходное уравнение имеет два корня:
исходное уравнение имеет два корня:
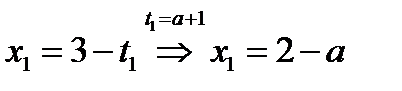 ,
, 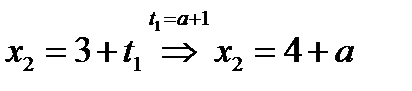 .
.
3) Уравнение (20.2) имеет один корень при тех значениях параметра 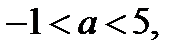 при которых графики функций
при которых графики функций 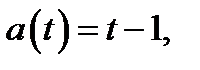
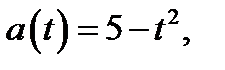 где
где 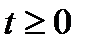 , пересекаются.
, пересекаются.
Точку пересечения графиков функций 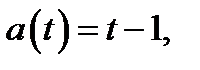
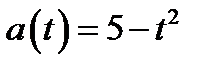 найдём из системы
найдём из системы
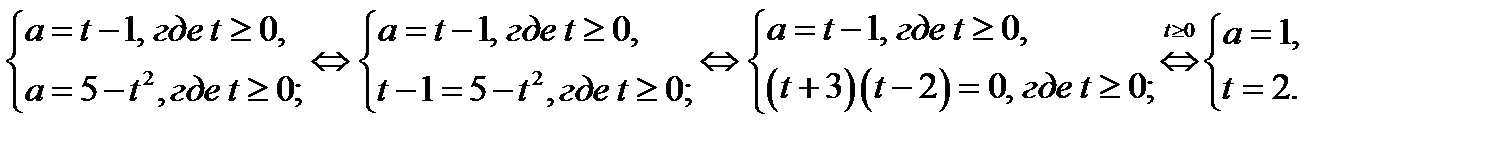 Из 2. следует, что при
Из 2. следует, что при 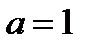 и
и 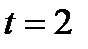 исходное уравнение имеет два корня:
исходное уравнение имеет два корня: 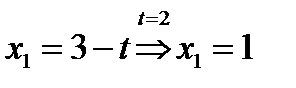 ,
, 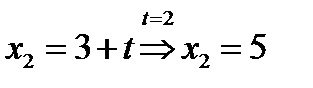 .
.
Ответ. 1) Три корня, если 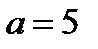 , то
, то 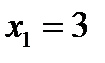 ,
, 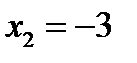 ,
, 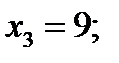 если
если 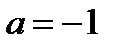 , то
, то 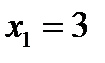 ,
, 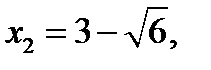
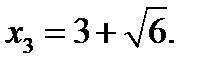
2) Два корня, если 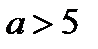 , то
, то 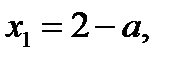 ,
, 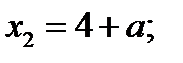 если
если 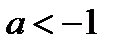 , то
, то 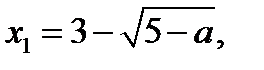
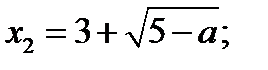 если
если 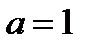 , то
, то 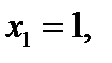 ,
, 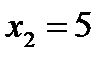 .
.
21.Найдите все значения параметра а, при каждом из которых уравнение 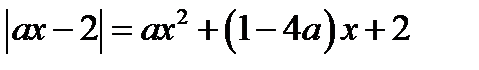 имеет единственный корень.
имеет единственный корень.
Решение. 1. При любом значении 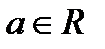 корнем уравнения является
корнем уравнения является 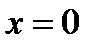 , так как в этом случае исходное уравнение принимает вид
, так как в этом случае исходное уравнение принимает вид 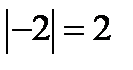 .
.
2. Уравнение имеет единственный корень при тех значениях параметра а, при которых оно имеет только корень 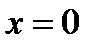 (так как
(так как 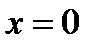 корень исходного уравнения при любом значении
корень исходного уравнения при любом значении 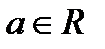 ).
).
а) Если 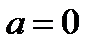 , то исходное уравнение имеет единственный корень
, то исходное уравнение имеет единственный корень 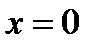 (так как уравнение принимает вид
(так как уравнение принимает вид 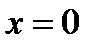 ).
).
б) Пусть 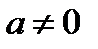 .
.
Исходное уравнение равносильно совокупности уравнений
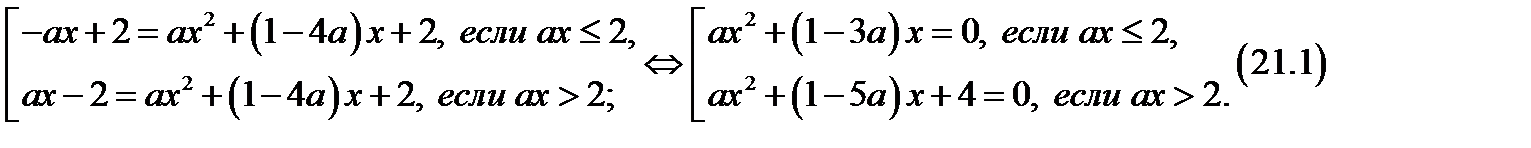 Рассмотрим первое уравнение совокупности (21.1), если
Рассмотрим первое уравнение совокупности (21.1), если 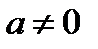 . Имеем
. Имеем
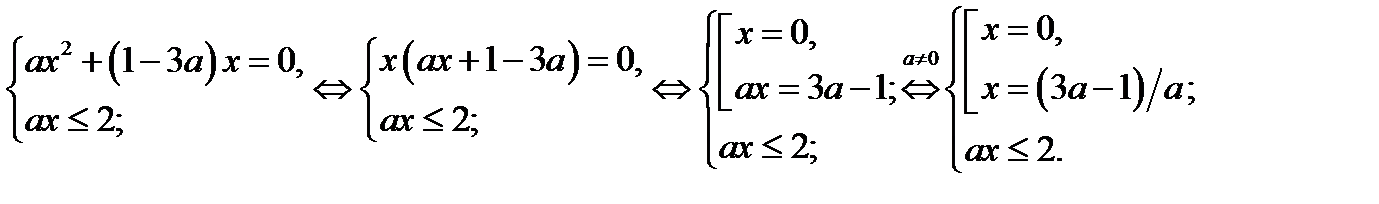
Из последней системы следует, что первое уравнение совокупности (21.1), имеет единственный корень 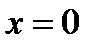 , если
, если 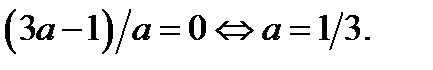 Отметим, что
Отметим, что 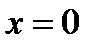 и
и 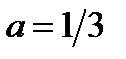 удовлетворяют условию
удовлетворяют условию 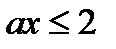 .
.
Корнем второго уравнение совокупности ( 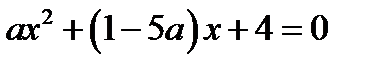 ) не является
) не является 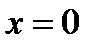 ни при каких значениях
ни при каких значениях 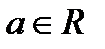 .
.
Итак, исходное уравнение при 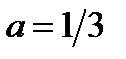 имеет единственный корень
имеет единственный корень
Ответ. 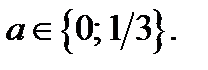
22.Найдите все значения параметра а, при каждом из которых уравнение 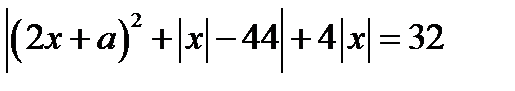 имеет три корня.
имеет три корня.
Решение. 1. Если 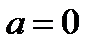 , то исходное уравнение принимает вид
, то исходное уравнение принимает вид
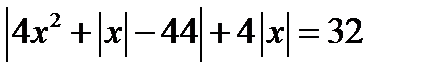 . (22.1)
. (22.1)
Уравнение (22.1) имеет нечётное число корней тогда и только тогда, когда 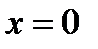 является корнем уравнения (так как
является корнем уравнения (так как 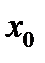 и
и  являются одновременно корнями уравнения). Легко проверить, что
являются одновременно корнями уравнения). Легко проверить, что 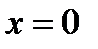 не является корнем уравнения (22.1), поэтому при
не является корнем уравнения (22.1), поэтому при 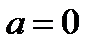 исходное уравнение не может иметь трёх корней.
исходное уравнение не может иметь трёх корней.
2. Пусть 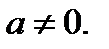
Перепишем уравнение в виде
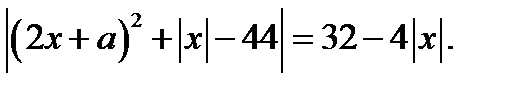
Так как 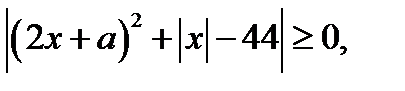 то последнее уравнение, а значит и исходное уравнение, имеет решение, если
то последнее уравнение, а значит и исходное уравнение, имеет решение, если 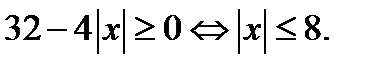
Итак, исходное уравнение имеет решение, если 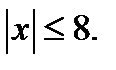
Замечание.Если точка 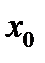 является корнем исходного уравнения при
является корнем исходного уравнения при 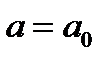 ,то
,то  является корнем этого уравнения при
является корнем этого уравнения при 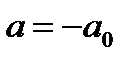 . Это следует из того, что
. Это следует из того, что 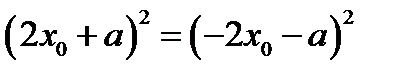 и
и 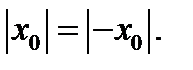
Из замечания следует: еслиисходного уравнения имеет три корня при 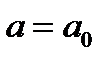 ,то оно имеет также три корня при
,то оно имеет также три корня при 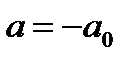 .
.
3. Рассмотрим исходное уравнение при 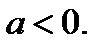
Исходное уравнение, если 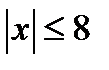 (так как
(так как 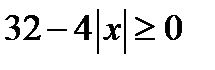 ) равносильно совокупности уравнений
) равносильно совокупности уравнений
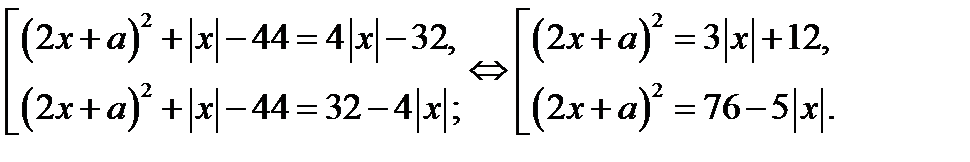
4. Рассмотрим функции 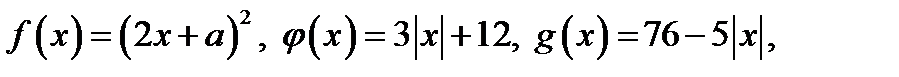 где
где 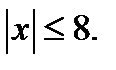
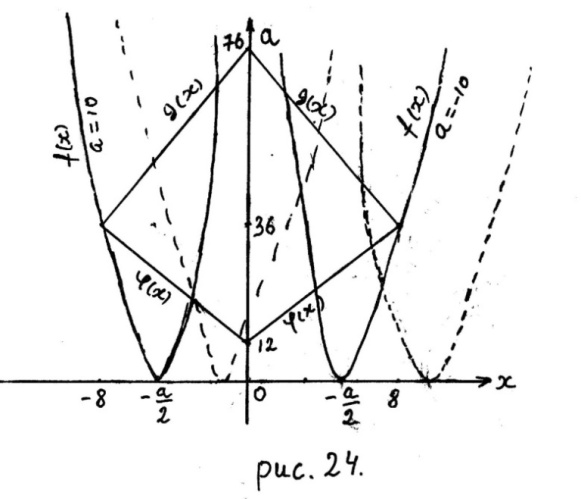 а) Графиком функции
а) Графиком функции 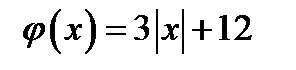 , где
, где 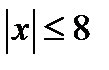 является «уголок» с вершиной в точке (0; 12). Очевидно,
является «уголок» с вершиной в точке (0; 12). Очевидно, 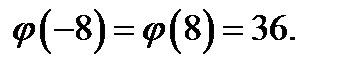
б) Графиком функции 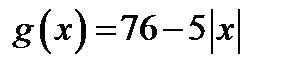 , где
, где 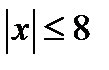 является «уголок» с вершиной в точке (0; 76). Очевидно,
является «уголок» с вершиной в точке (0; 76). Очевидно,