Неравенства с двумя переменными. Метод областей
Неравенство с двумя переменными в общем случае выглядит так:
f(x,y) V g(x,y), где V — знак ≤, ≥, <, >. (2).
Его ОДЗ — это общая часть областей определения функций f(x,y) и g(x,y), т. е. ОДЗ(2) = D(f) ∩ D(g). Решением неравенства (2) называется такая упорядоченная пара (х0, у0), что f(х0, у0) V g(х0, у0). Что для нахождения множества решений неравенства (2) удобно использовать аналог метода интервалов, который называется методом областей и представляет собой следующий алгоритм.
Для решения неравенства (2) достаточно сделать следующее.
Найти ОДЗ неравенства (2). Линии, не входящие в ОДЗ следует изобразить пунктирными. Изобразить на плоскости линии, являющиеся графиком уравнения 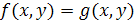 . В случае нестрогого знака (т. е. ≥ или ≤) неравенства (2) эти линии следует изобразить сплошными, если же знак неравенства (2) строгий (т. е. > или <), то пунктирными. Линии из предыдущих двух пунктов разбивают плоскость на области. Из каждой области следует выбрать по точке и подставить ее координаты в исходное неравенство (2) чтобы проверить: выполнено это неравенство в выбранной области, или нет. Заштриховать области, в которых неравенство (2) выполняется. . В случае нестрогого знака (т. е. ≥ или ≤) неравенства (2) эти линии следует изобразить сплошными, если же знак неравенства (2) строгий (т. е. > или <), то пунктирными. Линии из предыдущих двух пунктов разбивают плоскость на области. Из каждой области следует выбрать по точке и подставить ее координаты в исходное неравенство (2) чтобы проверить: выполнено это неравенство в выбранной области, или нет. Заштриховать области, в которых неравенство (2) выполняется. |
Замечание. Поскольку никакая из точек, лежащих на пунктирной линии, не может быть решением неравенства, точки пресечения сплошных и пунктирных линий на координатной плоскости следует изображать светлыми (или, что то же самое выколотыми).
Рассмотрим пример использования метода областей.
Пример 4. Решить методом областей неравенство 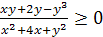 .
.
Решение.
ОДЗ этого неравенства состоит из всех точек координатной плоскости, удовлетворяющих неравенству 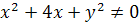 или
или 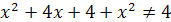 , т.е.
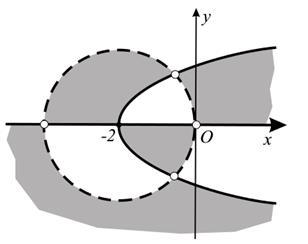
, т.е. 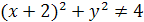 . Пунктирной линией изображаем окружность с центром в точке (-2,0) радиуса 2 (рис. 6).
. Пунктирной линией изображаем окружность с центром в точке (-2,0) радиуса 2 (рис. 6).
Решая уравнение, соответствующее данному неравенству, получим на ОДЗ 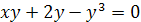 или
или 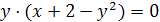 . Графиком последнего уравнения является ось Ох и парабола
. Графиком последнего уравнения является ось Ох и парабола 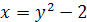 . Точки пересечения этих линий с пунктирной окружностью изображаем светлыми (рис. 6).
. Точки пересечения этих линий с пунктирной окружностью изображаем светлыми (рис. 6).
Нарисованные линии разбивают плоскость на восемь областей. Из каждой области выбираем по точке и подставляем их координаты в данное неравенство.
 (1,1)
(1,1) 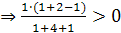 , т. е. неравенство выполняется.
, т. е. неравенство выполняется.
(1,-1) 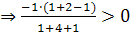 , т. е. неравенство выполняется.
, т. е. неравенство выполняется.
(1,10) 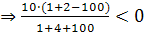 , т. е. неравенство не выполняется.
, т. е. неравенство не выполняется.
(1,-10) 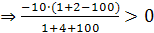 , т. е. неравенство выполняется.
, т. е. неравенство выполняется.
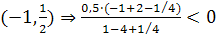 , т. е. неравенство не выполняется.
, т. е. неравенство не выполняется.
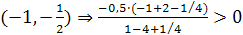 , т. е. неравенство выполняется.
, т. е. неравенство выполняется.
(-2,1) 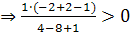 , т. е. неравенство выполняется.
, т. е. неравенство выполняется.
Замечание. При решении нестрогих неравенств с двумя переменными, также как и в случае одной переменной, могут получиться изолированные решения. Примером может служить неравенство 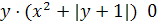 . Дело в том, что график уравнения
. Дело в том, что график уравнения 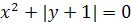 является только одна точка — (0,-1) (поскольку это уравнение может выполняться только в случае, когда одновременно
является только одна точка — (0,-1) (поскольку это уравнение может выполняться только в случае, когда одновременно 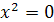 и
и 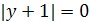 ). Поэтому решением неравенства
). Поэтому решением неравенства 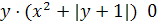 будет верхняя полуплоскость и одна точка нижней полуплоскости — (0,-1).
будет верхняя полуплоскость и одна точка нижней полуплоскости — (0,-1).
Задачи с параметром
Уравнения с параметрами. В общем случае уравнение с переменной х и параметром а имеет вид
F(x, a) = 0, (3)
где F(x, a) — некоторое алгебраическое выражение от х и а. Решением такого уравнения называется функция x = f(a), определенная на некотором множеств 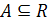 , при подстановке которой уравнение (3) превращается в тождество
, при подстановке которой уравнение (3) превращается в тождество
F(f(a), a) = 0 на всем множестве А. Решить уравнение (3) — это означает разбить всю действительную прямую R (область изменения параметра ) на множества А, В, С, …, на каждом из которых необходимо найти все решения этого уравнения, либо доказать, что решений не существует. Граничные точки множеств А, В, С, … принято называть критическими значениями параметра. Рассмотрим несколько примеров.
Пример 1. Решить уравнение 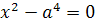 .
.
Решение. 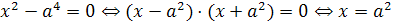 или
или 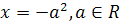 . В этом примере мы получили два решения
. В этом примере мы получили два решения 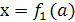 и
и 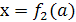 (где
(где 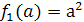 и
и 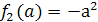 ), причем
), причем 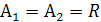 . Критических значений параметра нет.
. Критических значений параметра нет.
Ответ: 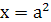 или
или 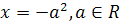
Пример 2. Решить уравнение 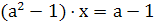 .
.
Решение. Для нахождения зависимости х от а необходимо разделить обе части этого уравнения на коэффициент при переменной х. Сначала рассмотрим случай, когда этот коэффициент обращается в ноль. При а = 1 получается уравнение 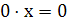 , справедливое при всех .
, справедливое при всех . 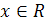 При а = - 1 получается уравнение
При а = - 1 получается уравнение 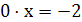 без корней. При всех остальных значениях параметра получаем
без корней. При всех остальных значениях параметра получаем 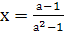 или
или 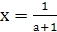 . В этом примере на множестве А = (- ∞; -1) U (- 1; 1) U (1; ∞) найдено решение
. В этом примере на множестве А = (- ∞; -1) U (- 1; 1) U (1; ∞) найдено решение 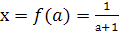 . На одноточечном множестве В = { - 1 } доказано,что нет решений, а на множестве С = { 1 } уравнение справедливо при всех
. На одноточечном множестве В = { - 1 } доказано,что нет решений, а на множестве С = { 1 } уравнение справедливо при всех 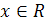 . Критическими значениями параметра являются
. Критическими значениями параметра являются 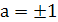 .
.
Ответ: при 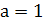 уравнение справедливо при всех х;
уравнение справедливо при всех х;
при 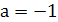 нет решений;
нет решений;
при 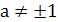 решением является
решением является 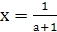 .
.
Пример 3. Решить уравнение 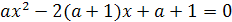 .
.
Решение. При а = 0 это уравнение превращается в линейное - 2х + 1 = 0 с корнем 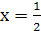 . Во всех остальных случаях уравнение будет квадратным, его дискриминант равен D = 4a + 4. Условию D ≥ 0 удовлетворяют все а ≥ - 1. Таким образом, при а < - 1 данное уравнение не имеет решений, а при
. Во всех остальных случаях уравнение будет квадратным, его дискриминант равен D = 4a + 4. Условию D ≥ 0 удовлетворяют все а ≥ - 1. Таким образом, при а < - 1 данное уравнение не имеет решений, а при 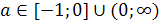 используя формулу корней квадратного уравнения, получаем
используя формулу корней квадратного уравнения, получаем 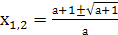 . В этом примере на множестве А = [- 1; 0) U (0; ∞) было найдено два решения
. В этом примере на множестве А = [- 1; 0) U (0; ∞) было найдено два решения 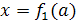 и
и 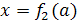 (где
(где 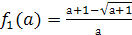 и
и 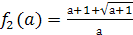 ), на одноточечном множестве В = {0} решение уравнения единственно -
), на одноточечном множестве В = {0} решение уравнения единственно - 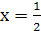 и, наконец, при всех значений параметра из множества С = (-∞; - 1) уравнение не имеет решений. Критическими значениями параметра являются а = -1 и а = 0.
и, наконец, при всех значений параметра из множества С = (-∞; - 1) уравнение не имеет решений. Критическими значениями параметра являются а = -1 и а = 0.
Ответ: при а = 0 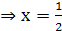 ;
;
при а < - 1 нет решений;
при остальных значениях параметра решениями являются 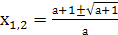
Метод, с помощью которого были решены три предыдущих задачи, можно назвать алгебраическим. В этих примерах с помощью простых алгебраических преобразований от исходного уравнения по цепочке равносильных уравнений мы приходим к уравнению 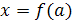 (или совокупности уравнений), которое является решением уравнения с параметром. В дальнейшем мы будем использовать графический способ решения уравнений с параметром, который заключается в следующем.
(или совокупности уравнений), которое является решением уравнения с параметром. В дальнейшем мы будем использовать графический способ решения уравнений с параметром, который заключается в следующем.
1.  От уравнения F(x, a) = 0 перейти к системе F(x, y) = 0, y = a. 2. На плоскости хОу построить график уравнения F(x, y) = 0. 3. Пересечь прямую у = а с графиком уравнения F(x, y) = 0 и спроецировать это пересечение на ось Ох (т.е., фактически, найти первые координаты точек пересечения прямой у = а с графиком уравнений F(x, y) = 0). От уравнения F(x, a) = 0 перейти к системе F(x, y) = 0, y = a. 2. На плоскости хОу построить график уравнения F(x, y) = 0. 3. Пересечь прямую у = а с графиком уравнения F(x, y) = 0 и спроецировать это пересечение на ось Ох (т.е., фактически, найти первые координаты точек пересечения прямой у = а с графиком уравнений F(x, y) = 0). |
Решим графическим способом следующую задачу
Пример 4. Решить уравнение |2x — 1| + |x — 3 | = x + a.
 Решение. 1. Перейдем к системе |2x — 1| + |x — 3 | = x + у,
Решение. 1. Перейдем к системе |2x — 1| + |x — 3 | = x + у,
у = а.
2. Необходимо построить график уравнения |2x — 1| + |x — 3 | = x + у или
у = |2x — 1| + |x — 3 | - x . Нулями подмодульных выражений будут 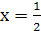 и
и
х = 3. Знаки подмодульных выражений на каждом из трех промежутков определяются без труда.
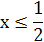 | 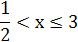 | 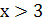 | |
| 2х — 1 | - | + | + |
| х — 3 | - | - | + |
Раскрывая модули на каждом из трех промежутков, получим
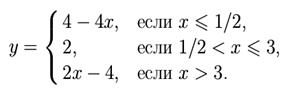
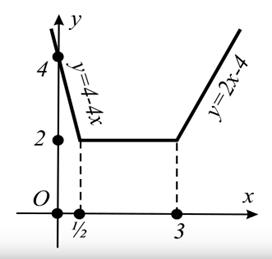 График этой функции изображен на рисунке.
График этой функции изображен на рисунке.
3. Пересекая прямую у = а с графиком уравнения, замечаем, что возможны три различных случая.
При а < 2 пересечение пусто и данное уравнение решений не имеет. При а = 2 пересечением является отрезок и его проекция на ось Ох являются 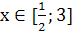 . Наконец, при а > 2 будут две точки пересечения. Первая точка определяется из системы у = 4 — 4х и
. Наконец, при а > 2 будут две точки пересечения. Первая точка определяется из системы у = 4 — 4х и
у = а, ее первая координата находится из уравнения 4 — 4х = а и 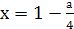 . Вторая точка определяется из системы у = 2х — 4 и у = а, ее первая координата находится из уравнения 2х — 4 = а и равна
. Вторая точка определяется из системы у = 2х — 4 и у = а, ее первая координата находится из уравнения 2х — 4 = а и равна 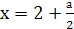 .
.
Ответ: при а < 2 нет решений;
при а = 2 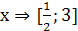 ;
;
при а > 2 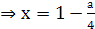 или
или 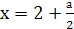 .
.
Замечание. Плоскость хОу предпочтительнее плоскости хОа в графическом способе решения по следующим двум причинам. Во-первых, прямая у = а в плоскости хОу обозначает горизонтальную прямую, в плоскости хОа уравнение а = а задает всю плоскость и формально преодолеть это затруднение непросто. Во-вторых, в уравнение с параметром F(x, a) = 0 переменные х и а входят не равнозначно. Связано это с необходимостью выразить х через а, а не наоборот. В плоскости хОа разный «статус» переменных х и а теряется, в то же время переход к системе F(x, a) = 0 и у = а сохраняет информацию о том, что а является параметром.
Заключение.
В результате выполненной работы мы выяснили, что метод интервалов не только широко используется для решения многих неравенств, но для и исследования многих задач повышенной трудности. Метод областей позволяет эффективно строить множества точек на координатной плоскости.
Также было показано, что метод областей может быть более эффективен, чем метод интервалов при решении уравнений и неравенств с параметром, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра.
В процессе исследования был систематизирован теоретический материал по проблемам неравенств с двумя неизвестными и системам неравенств с двумя неизвестными. Практически выработаны методики решения задач на нахождение: множества точек плоскости, координаты, которых удовлетворяют данному неравенству; площади фигуры ограниченной неравенством; значений параметра.
Результаты данной работы могут быть использованы для приобретения опыта решения задач с использованием метода областей, для повышения уровня логической культуры и для более глубокой подготовки к ЕГЭ.
Список использованной литературы:
1)Математика для поступающих в серьезные вузы. О.Ю.Черкасов , А.Г.Якушев . – M.: Московский лицей, 2009.
2)ЕГЭ 2010 математика .Федеральный институт педагогических измерений. Официальный разработчик контрольных измерительных материалов для ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА. Общая редакция: А.Л.Семенов, И.В.Ященко.
3) http://ege-study.ru/materialy-ege/metod-intervalov/
4) http://school-collection.edu.ru/catalog/rubr/49e3d8f3-baf8-4599-b6e3-b9fe79594e71/82292/
