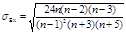Асимметрия и эксцесс распределения
Выяснение общего характера распределения предполагает оценку его однородности, а так же вычисления показателей асимметрии и эксцесса.
Асимметрия представляет собой отклонение эмпирического ряда распределения от симметричной формы и рассчитывается несколькими способами:
• асимметрия первого порядка – разность между средней арифметической величиной и модой, которая является асимметрией первого порядка (показатель асимметрии Пирсона): : 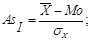
• асимметрия второго порядка рассчитывается по формулам: ;
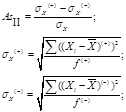
• асимметрия третьего порядка представляет собой нормированный центральный момент третьего порядка: отношение центрального момента 3-го порядка к кубу среднего квадратического отклонения:
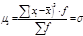
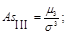 Тогда
Тогда 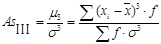 .
.
Тогда .
Коэффициент асимметрии характеризует асимметричность распределения признака в совокупности:
если 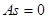 , то распределение симметричное,
, то распределение симметричное,
если 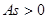 , то асимметрия правосторонняя,
, то асимметрия правосторонняя,
если 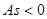 , то асимметрия левосторонняя.
, то асимметрия левосторонняя.
Величина 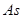 может изменяться от -1 до +1 (для одновершинных распределений).
может изменяться от -1 до +1 (для одновершинных распределений).
Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.
Для симметричных распределений среднее арифметическое значение, мода и медиана равны между собой. Для левосторонней асимметрии Mo < Me < 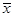 . Для правосторонней асимметрии Mo > Me > .
. Для правосторонней асимметрии Mo > Me > .
С помощью момента 4-го порядка характеризуется свойство рядов распределения, называемое эксцессом. Он рассчитывается для умеренно асимметричных распределений. Эксцесс представляет собой отклонение вершины эмпирического распределения вверх или вниз от вершины. кривой нормального распределения. Показатель эксцесса рассчитывается по формуле:
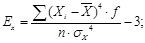
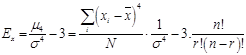
Наличие положительного эксцесса свидетельствует о крутизне (однородности) распределения и означает, что распределение более островершинное, а при отрицательном эксцессе – распределение имеет более плосковершинный характер, чем нормальное, что свидетельствует о пологости, разнородности данных. Для нормального распределения отношение , 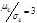 следовательно, эксцесс равен нулю.
следовательно, эксцесс равен нулю.
По значениям показателей симметрии и эксцесса распределения можно судить о близости распределения к нормальному, что бывает существенно важно для оценки результатов корреляционно-регрессионного анализа, возможностей вероятностной оценки прогнозов.
Для оценки существенности асимметрии и эксцесса вычисляют показатели среднеквадратической ошибки:
- среднеквадратическая ошибка показателя асимметрии: , : 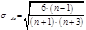 ,где
,где 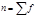 .
.
- среднеквадратическая ошибка показателя эксцесса: