IV. Кинематический анализ плоского механизма.
Задание К.3.
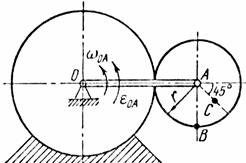
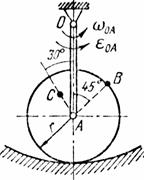
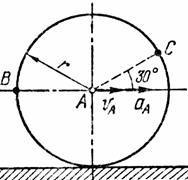
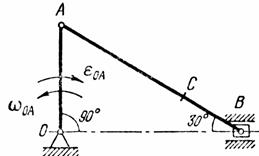
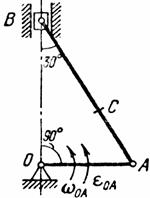
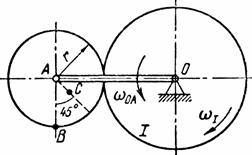
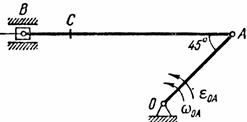
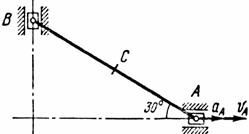
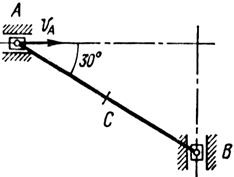
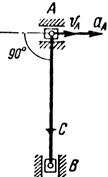
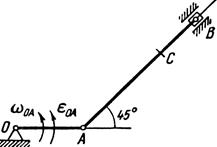
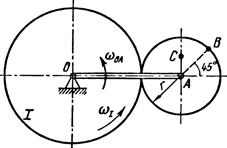
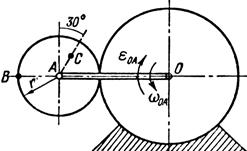
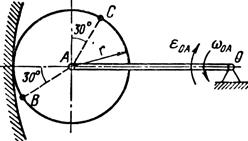
Найти для заданного положения механизма скорости и ускорения точек В и С, а также угловую скорость и угловое ускорение звена, котором) эти точки принадлежат. Схемы механизмов помещены на рис. 12-14, а необходимые для расчета данные приведены в табл. 7.
Таблица 7
| Номер варианта (рис. 12-14) | Размеры, см | woa рад/с | wI рад/с | eOA рад/с2 | va, см/с | аА, см/с2 | ||||||||||||||
| ОА | r | АВ | АС | |||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | — | — | |||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| _ | — | — | — | — | ||||||||||||||||
| — | — | — | ||||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | _ | — | — | — | ||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | _ | — | — | — | ||||||||||||||||
| — | _ | — | — | — | ||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | ||||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | 2,5 | — | — | |||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| — | - | — | — | |||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | 1,2 | — | — | |||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | |||||||||||||||||
| — | — | — | — | — | ||||||||||||||||
Примечание. wА и eOA — угловая скорость и угловое ускорение кривошипа ОА при заданном положении механизма; wI — угловая скорость колеса I (постоянная); vA и аA — скорость и ускорение точки А. Качение колес происходит без скольжения.
 |  | ||
 |  | ||
 |  | ||
 |  | ||
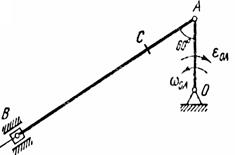 | 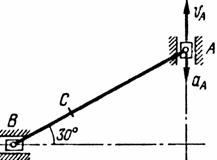 |
Рис. 12
 |  | ||
 |  | ||
 |  | ||
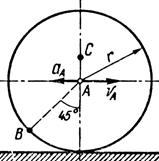 | 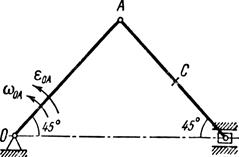 | ||
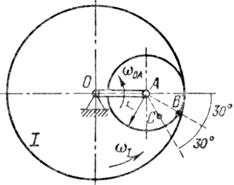 | 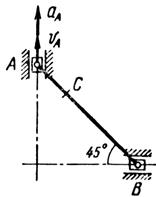 |
Рис. 13
 |  | ||
 |  | ||
 |  | ||
 |  | ||
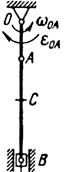 | 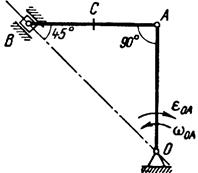 |
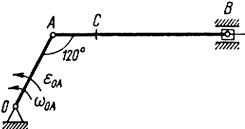
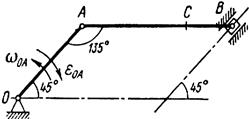
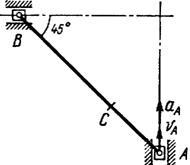
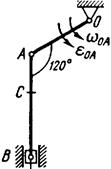
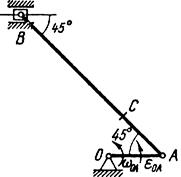
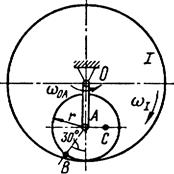
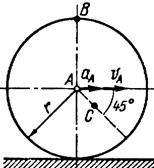
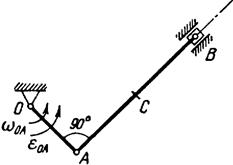
Рис. 14
Пример выполнения задания. Дано: схема механизма в заданном положении (рис. 15); исходные данные (табл. 8).
Таблица 8
| Размеры, см | woa, рад/с | eOA рад/с2 | ||
| ОА | АВ | АС | ||
| 1,5 |
Р е ш е н и е. 1. Определение скоростей точек и угловой скорости звена (рис. 16). Вычисляем модуль скорости пальца А кривошипа ОА при заданном положении механизма:
va=woa ОА.
Скорость точки А перпендикулярна кривошипу ОА. Скорость ползуна В направлена по вертикали. Мгновенный центр скоростей РАВ шатуна АВ находится в точке пересечения перпендикуляров, проведенных из точек А и В к их скоростям.
Угловая скорость звена АВ
wАВ= vA/APAB.
Модули скоростей точек В и С
VВ=wАВ•ВРАВ; vС=wАВ•CPAВ
Расстояния АРАВ, ВРАВ и СРАВ определяются из рассмотрения треугольников АВРАВ и АСРАВ:
АРАВ=52,0 см; ВРАВ=30,0 см; СРАВ=36,1 см.
В соответствии с этим vA=15,0 см/с; wAB=0,29 рад/с; vB=8,7 см/с; vс = 10,5 см/с.
Вектор 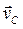 направлен перпендикулярно отрезку СРАВ в сторону, соответствующую направлению вращения звена AB.
направлен перпендикулярно отрезку СРАВ в сторону, соответствующую направлению вращения звена AB.
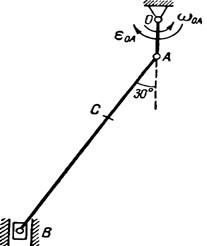 | 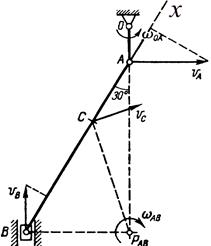 |
| Рис. 15 | Рис. 16 |
Для проверки определим скорость точки В другим способом. Воспользуемся теоремой о равенстве проекции скоростей точек на ось, проведенную через эти точки.
Направим ось х вдоль шатуна АВ в направлении от В к А.
Имеем va cos ( 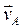 , х) = vb cos
, х) = vb cos 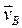 , x), или, как видно из рис. 16,
, x), или, как видно из рис. 16,
vA cos 60° = vB cos 30°.
Отсюда
vB = 8,7 см.
Полезно убедиться, что и найденная ранее скорость точки С удовлетворяет этой теореме.
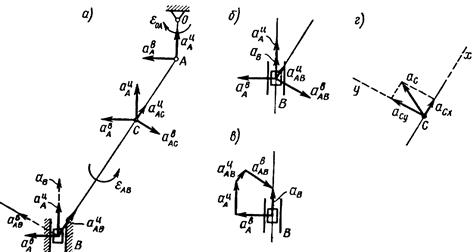 |
| Рис. 17 |
2. Определение ускорений точек и углового ускорения звена (рис. 12). Ускорение точки А складывается из вращательного и центростремительного ускорений:
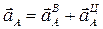 ;
; 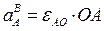 ;
; 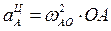
Согласно теореме об ускорениях точек плоской фигуры,
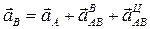 ,
,
или
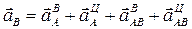 (1)
(1)
Центростремительное ускорение точки В во вращательном движении шатуна АВ вокруг полюса А
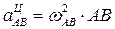
По приведенным формулам вычисляем:
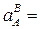 20,0 см/с2;
20,0 см/с2; 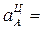 22,5 см/с2;
22,5 см/с2; 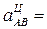 5,0 см/с2.
5,0 см/с2.
Вектор 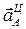 направлен от А к О. Вектор
направлен от А к О. Вектор 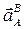 перпендикулярен вектору
перпендикулярен вектору 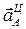 и направлен противоположно vA (вращение кривошипа ОА – замедленное).
и направлен противоположно vA (вращение кривошипа ОА – замедленное).
Вектор 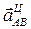 направлен от В к A. Что касается ускорения
направлен от В к A. Что касается ускорения 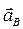 точки В и вращательного ускорения
точки В и вращательного ускорения 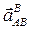 , то известны только линии действия этих векторов:
, то известны только линии действия этих векторов: 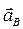 — по вертикали вдоль направляющих ползуна,
— по вертикали вдоль направляющих ползуна, 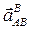 — перпендикулярно АВ.
— перпендикулярно АВ.
Зададимся произвольно их направлениями по указанным линиям (рис. 17, а). Эти ускорения определим из уравнений проекций векторного равенства (1) на оси координат. Знак в ответе показывает, соответствует ли истинное направление вектора принятому при расчете.
Выбрав направление осей х и у, как показано на рис. 17, а, получаем:
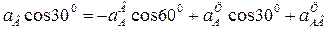 (2)
(2)
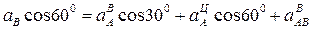 (3)
(3)
Из уравнения (2) находим
aВ = 16,7 см/с2.
Ускорение ав направлено, как показано на рис. 17, а. Из уравнения (3) получаем
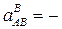 20,2 см/с2.
20,2 см/с2.
Направление 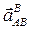 противоположно показанному на рис. 17, а.
противоположно показанному на рис. 17, а.
Ускорение 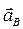 и все его составляющие с учетом их истинных направлений и масштаба показаны на рис. 17, б.
и все его составляющие с учетом их истинных направлений и масштаба показаны на рис. 17, б.
Угловое ускорение шатуна АВ с учетом того, что здесь 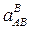 — алгебраическая величина, определяется по формуле
— алгебраическая величина, определяется по формуле
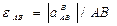 .
.
Вычисляя, находим
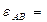 0,34 рад/с2.
0,34 рад/с2.
Направление ускорения 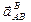 относительно полюса А определяет направление углового ускорения
относительно полюса А определяет направление углового ускорения 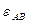 . Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном — противоположно ему. В данном случае угловое ускорение противоположно направлению вращения шатуна.
. Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном — противоположно ему. В данном случае угловое ускорение противоположно направлению вращения шатуна.
Определить 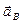 и
и 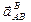 можно и графически – построением многоугольника ускорений.
можно и графически – построением многоугольника ускорений.
Отложим из точки В согласно (1) в выбранном масштабе последовательно векторы 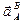 ,
, 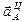 и
и 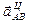 (рис. 17, в). Через конец вектора
(рис. 17, в). Через конец вектора 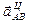 проведем прямую, параллельную вращательному ускорению
проведем прямую, параллельную вращательному ускорению 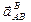 , т. е. перпендикулярно АВ, до пересечения ее с прямой, по которой направлено ускорение
, т. е. перпендикулярно АВ, до пересечения ее с прямой, по которой направлено ускорение 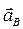 .
.
Последнее определяется как замыкающая сторона многоугольника ускорений.
Модули аВ и аВАВ могут быть найдены измерением на чертеже.
Определяем ускорение точки С:
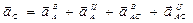
Вращательное и центростремительное ускорения точки С во вращательном движении АВ вокруг полюса А
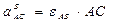 ,
, 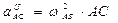
или
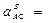 6,8 см/с2,
6,8 см/с2, 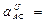 1,7 см/с2
1,7 см/с2
Вектор 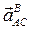 перпендикулярен вектору
перпендикулярен вектору 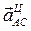 и направлен соответственно угловому ускорению
и направлен соответственно угловому ускорению 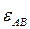 .
.
Ускорение точки С находим способом проекций (рис. 17, а):
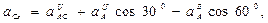
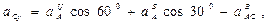
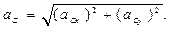
В результате вычислений получаем: аСх=11,2 см/с2; aCv = 21,8 см/с2; ас = 24,5 см/с2 (рис. 17, г).
Приведем решение этой же задачи другим, более общим методом.
На рис. 18 показана схема механизма в некотором произвольном положении.
Проведем оси координат. Уравнениями связи для данного механизма являются условия
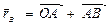 (4)
(4)
( 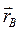 радиус-вектор точки B, проведенный из центра O),
радиус-вектор точки B, проведенный из центра O),
хв = а = const. (5)
Проецируя (4) на ось х, с учетом (5) имеем 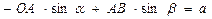 (6) Для определения угловой скорости звена АВ (6) Для определения угловой скорости звена АВ 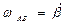 и углового ускорения и углового ускорения 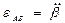 нет необходимости выражать нет необходимости выражать 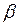 из (6). Проще непосредственно дважды продифференцировать (6). Имея в виду, что из (6). Проще непосредственно дважды продифференцировать (6). Имея в виду, что 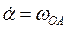 , получаем в результате первого дифференцирования , получаем в результате первого дифференцирования 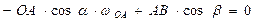 . (7) Отсюда . (7) Отсюда 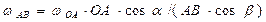 . (8) Дифференцируя (7) и учитывая, что . (8) Дифференцируя (7) и учитывая, что 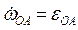 , имеем , имеем | 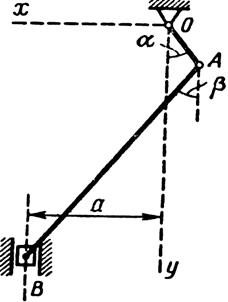 |
| Рис. 18 |
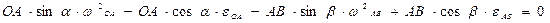
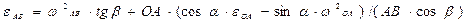 (9)
(9)
Выражения (8) и (9) позволяют вычислять 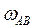 и
и 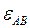 для любого положения механизма, в частности для заданного (a=0°, b=30°).
для любого положения механизма, в частности для заданного (a=0°, b=30°).
Заметим, что 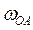 и
и 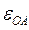 входят в эти выражения со знаком «+» или «–» в соответствии с принятым направлением отсчета угла а. В данном случае
входят в эти выражения со знаком «+» или «–» в соответствии с принятым направлением отсчета угла а. В данном случае 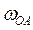 =1,5 рад/с,
=1,5 рад/с, 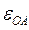 = -2,0 рад/с2. Смысл знаков
= -2,0 рад/с2. Смысл знаков 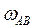 и
и 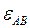 определяется направлением отсчета угла b.
определяется направлением отсчета угла b.
Модуль скорости точки В 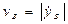 .Модуль ускорения
.Модуль ускорения 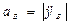 . Проецируя (4) на ось у, получаем
. Проецируя (4) на ось у, получаем
ув=ОA cos a + АВ cos b.
