Принужденной (гармонической) и свободной (экспоненты)

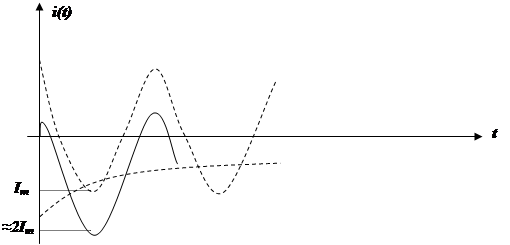
Токи при переходных процессах в какие-то моменты времени могут быть больше, чем в установившемся режиме почти в 2 раза, если свободная составляющая изменяется медленно относительно периода принужденной. Это следует учитывать при работе устройств.

Анализ переходных процессов в последовательной RLC-цепи

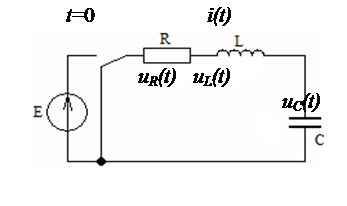
Подключение источника постоянного

напряжения

1) Определим начальные условия:

А) независимые

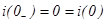
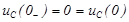
Б) зависимые

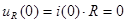
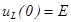(L –хх, C – кз u_R(0)+u_L(0)+u_C(0)=Е)

2) Уравнения: 0<t<∞ u_R(t)+u_L(t)+u_C(t)=e(t)=Е

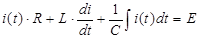
Характеристическое уравнение:

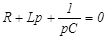
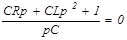
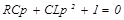p²+(R/L)p+1/(LC)=0

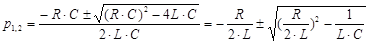
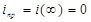(С – разрыв)

,

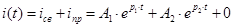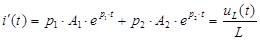
Определим коэффициенты А₁ и А₂ .

При t=0 ,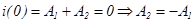

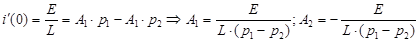
Окончательно получаем:

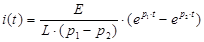
Проверка

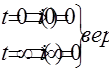(корни р_1,2<0). Найдем время и величину максимума тока

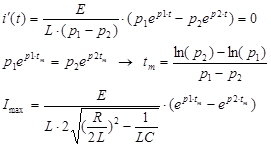
4) Определим напряжения u_R, u_L, u_C.

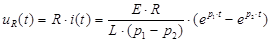
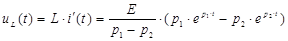При t=t_m u_L(t_m)=0

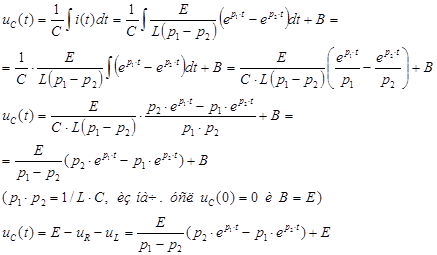
В зависимости от сопротивления R различают различные режимы переходного процесса цепи.

1) 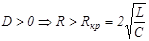. Получаем, что p₁ и p₂ – вещественные, отрицательные и 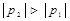, поэтому 2 экспонента быстрее изменяется.

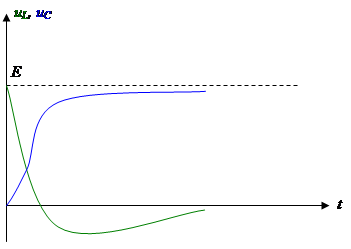
Такой режим работы называют апериодическим. Здесь емкость заряжается до Е и ток после этого прекращается.

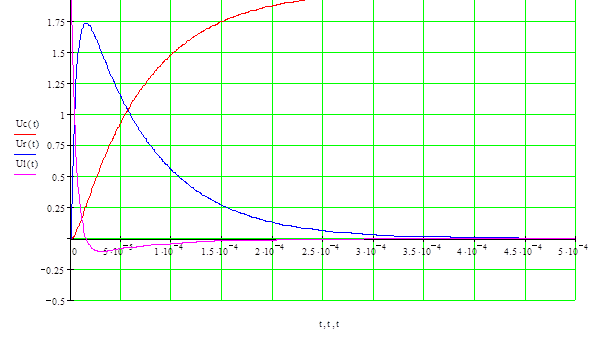
Расчетные графики при Е=2В в апериодическом режиме

2) R=R_кр – критический режим работы

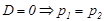=р= - R/2L<0

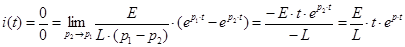
Графики примерно такие же, но более резкие.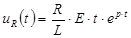

,

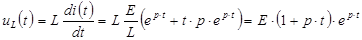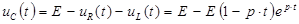
3)

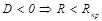
Корни p₁ и p₂ комплексно сопряженные.

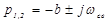, где 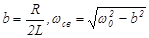- частота свободных колебаний (ω₀= 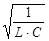– резонансная частота). С учетом

p₁-p₂=2∙j ∙ω_св

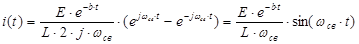- убывающая по экспоненте синусоида.

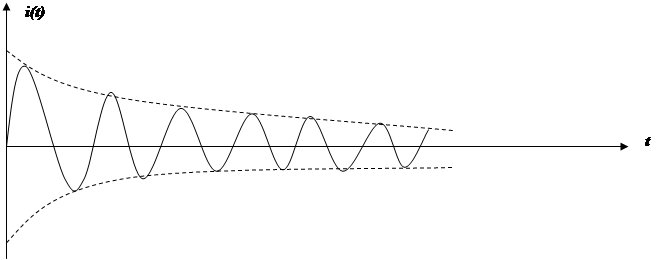
Режим переходного процесса называется колебательным. Происходит зарядка и разрядка конденсатора. В цепи происходит обмен электрической энергии емкости и магнитной энергии индуктивности. При этом ток меняет знак.

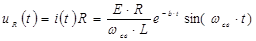– переходное напряжение на резисторе;

,

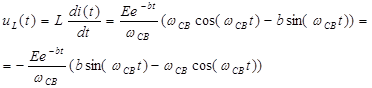
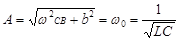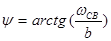
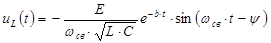– переходное напряжение на индуктивности.

Найдем выражение для емкости .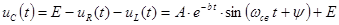

Составим второе уравнение для определения неизвестных коэффициентов:

.

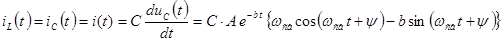Из нулевых начальных условий i(0)=0 , u_C(0)=0 получим систему уравнений:

, , .

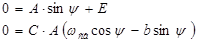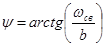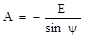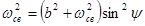, откуда .

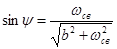следовательно .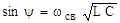

, ,

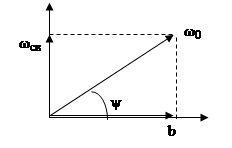
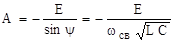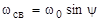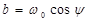. Переходное напряжение

на емкости:

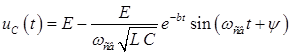, где ;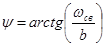

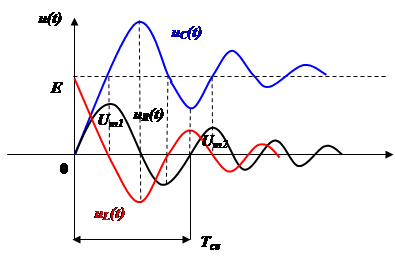Представим на графике соответствующие переходные напряжения:

Квазипериод свободных

колебаний: .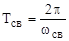

Декремент ослабления

(затухания):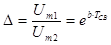

Логарифмический декремент затухания: .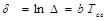

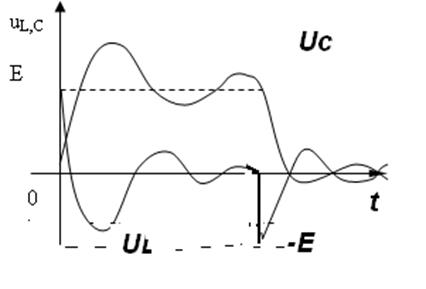
Напряжение при колебательном режиме может превысить ЭДС при переходном процессе – это надо учитывать.

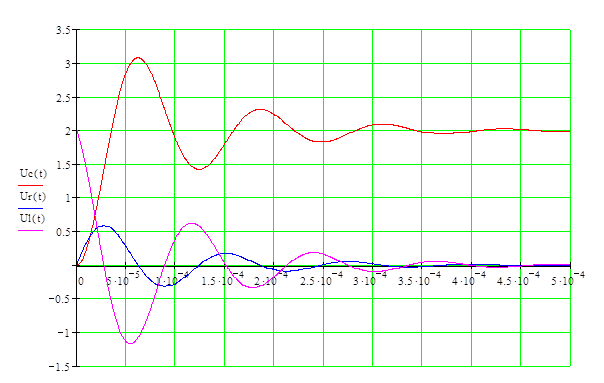
Расчетные графики при Е=2в в колебательном режиме

Отключение источника в последовательной RLC-цепи

Все процессы идут в обратном направлении: емкость разряжается. Характер процесса также определяется корнями характеристического уравнения (сравниваются R и R_кр). Ток меняет направление, соответственно u_R(t) и u_L(t) меняют знак, а u_C(t) остается того же знака.

Расчет сложных схем классическим методом

Для расчета сложных схем составляется большая система уравнений и решается. Но в инженерном плане классическим методом сложные цепи не рассчитывают из-за того, что получается большая система уравнений, да нужно решать еще одну систему уравнений для нахождения множителей экспонент и принужденных составляющих. Поэтому были разработаны другие методы.

2. Операторный метод расчёта переходных процессов. Преобразования Лапласа. Законы Кирхгофа в операторной форме

Преобразования Лапласа

Вначале операторный метод был разработан английским инженером Хевисайдом, а затем был обоснован математиками. Этот метод можно подразделить на собственно операторный метод и метод на основе преобразований Лапласа.

В операторном методе вводятся специальные операторы и правила действия с ними. Например, операцию дифференцирования переводят в операцию умножения на некоторый символ или оператор p, а интегрирования – в операцию деления на оператор p. Преобразование Лапласа (прямое) определяется интегралом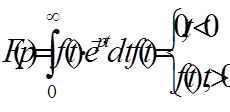

f(t) – оригинал, F(p)- изображение по Лапласу,

р - комплексная частота (комплексная переменная) p=δ+jω.

Оригинал должен возрастать не быстрее экспоненты, f(t)=0 при t<0. Размерность изображения соответствует размерности функции, умноженной на секунду.

Не должно быть скачков ∞ разрыва в оригинале. Допускаются конечные скачки.