Вывод аналитического выражения выходной функции в форме преобразований Лапласа
Преобразуем по Лапласу при нулевых начальных условиях полученное выше дифференциальное уравнение трёхкоординатной системы управления 
, используя следующую теорему.
Теорема:
Пусть 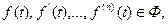 где Ф-класс преобразуемых по Лапласу функций, тогда справедливо следующее преобразование  |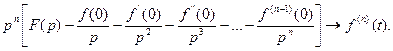
В результате преобразования при равных нулю возмущающем воздействии и его производных получим:
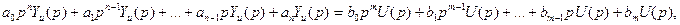отсюда 
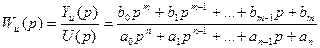- передаточная функция по каналу управления;
если в уравнении (3) принять входное воздействие и его производные равными нулю, то получим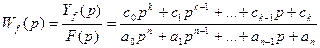 
- передаточная функция по каналу возмущения.
Знаменатель передаточной функции называют характеристическим полиномом, а, приравняв знаменатель к нулю, получим характеристическое уравнение. Корни знаменателя называются полюсами, а корни числителя – нулями.
Передаточная функция зависит от конструкции устройства и свойств материала конструкции, но не зависит от входных воздействий и выходной функции.
Запасы устойчивости
Для нормального функционирования всякая САР должна быть удалена от границы устойчивости и иметь достаточный запас устойчивости. Необходимость этого обусловлена следующими причинами:
1. Уравнения элементов САР, как правило, идеализированы, при их составлении не учитывают второстепенные факторы;
2. При линеаризации уравнений погрешности приближения дополнительно увеличиваются;
3. Параметры элементов определяют с некоторой погрешностью;
4. Параметры однотипных элементов имеют технологический разброс;
5. При эксплуатации параметры элементов изменяются вследствие старения.
В практике инженерных расчетов наиболее широко используют определение запаса устойчивости на основе критерия НАЙКВИСТА, по удалению АФХ разомкнутой системы от критической точки с координатами (-1, j0), что оценивают двумя показателями: запасом устойчивости по фазе g и запасом устойчивости по модулю (по амплитуде) H.
Для того чтобы САР имела запасы устойчивости не менее g и H, АФХ ее разомкнутой цепи при удовлетворении критерия устойчивости не должна заходить в часть кольца, заштрихованного на рис. 1, где H определяется соотношением 
 | |||
 | |||
|
|
`  |  | ||
Если устойчивость определяется по ЛЧХ условно-устойчивых систем, то для обеспечения запасов устойчивости не менее g и h необходимо, чтобы:
а) при h ³ L ³ -h фазо-частотная характеристика удовлетворяла неравенствам θ > -180°+g или θ < -180°-g, т.е. не заходила в заштрихованную область 1 на рис. 2;
б) при -180°+g ³ θ ³ -180°-g амплитудно-частотная характеристика удовлетворяла неравенствам L < -h или L > h, т.е. не заходила в заштрихованные области 2' и 2'' на рис. 2.
Для абсолютно устойчивой системы запасы устойчивости g и h определяют так, как показано на рис. 3:
1. Запас по фазе 
2. Запас по модулю h=-L(ω-π), где ω-π – частота, при которой θ=-180˚.
Необходимые значения запасов устойчивости зависит от класса САР и требований к качеству регулирования. Ориентировочно должно быть g=30¸60° и h=6¸20дБ.
Минимально допустимые запасы устойчивости по амплитуде должны быть не менее 6дБ (то есть передаточный коэффициент разомкнутой системы в два раза меньше критического), а по фазе не менее 25¸30°.