Множество простых процессоров

Основные компоненты

Нейронная сеть является совокупностью элементов, соединенных не­которым образом так. чтобы между ними обеспечивалось взаимодействие. Эти элементы, называемые также нейронами или узлами, представ­ляют собой простые процессоры, вычислительные возможности которых обычно ограничиваются некоторым правилом комбинирования входных сигналов и правилом активизации, позволяющим вычислить выходной сигнал по совокупности входных сигналов. Выходной сигнал элемента может посылаться другим элементам по взвешенным связям, с каждой из которых связан весовой коэффициент или вес. В зависимости от значения весового коэффициента передаваемый сигнал или усиливается, или по­давляется. Элемент нейронной сети схематически показан на рис. 1.1.

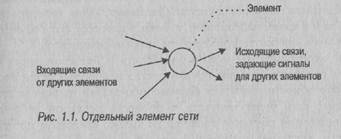
Рис.1.1.Отдельный элемент сети

Один из самых привлекательных аспектов использования нейронных сетей заключается в том, что, хотя элементы такой сети имеют очень ограниченные вычислительные возможности, вся сеть в целом, объединяя большое число таких элементов, оказывается способной выполнять довольно сложные задачи (рис. 1.2).

Входные элементы, принимающие данные от датчиков информации

Один выходной элемент, являющийся индикатором технического состояния.

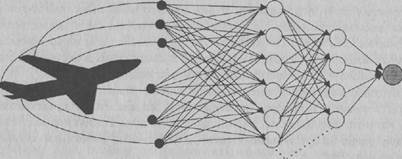
Рис. 1.2. Схема применения нейронной сети для контроля технического состояния авиалайнера. Связи элементов показаны стрелками. Входные элементы получают информацию непосредственно от датчиков, установленных на борту самолета. Вы­ходной элемент является индикатором технического состояния летательного аппарата

Структура связей отражает детали конструкции сети, а именно то, какие-элементы соединены, в каком направлении работают соединения и каков уровень значимости (т.е. вес) каждого из соединений. Задача, которую по­нимает сеть (или ее программа), описывается в терминах весовых значений связей, связывающих элементы. Структура связей обычно определяется в два этапа: сначала разработчик системы указывает, какие элементы должны быть связаны и в каком направлении, а затем в процессе фазы обучения оп­ределяются значения соответствующих весовых коэффициентов.

Весовые коэффициенты можно определить и без проведения обуче­ния, но как раз самое большое преимущество нейронных сетей заключа­ется в их способности обучаться выполнению задачи на основе тех дан­ных, которые сеть будет получать в процессе реальной работы. Для многих приложений обучение является не только средством программи­рования сети, когда нет достаточных знаний о способе решения задачи, позволяющих выполнить программирование в традиционной форме, но часто единственной целью обучения является проверка того, что сеть действительно сможет научиться решать поставленные перед ней задачи. Существует множество различных типов нейронных сетей, но все рас­сматриваемые в данной книге сети обладают рядом общих характери­стик, которые можно представить с помощью следующих абстракций.

• Множество простых процессоров

• Структура связей

• Правило распространения сигналов в сети

• Правило комбинирования входящих сигналов

• Правило вычисления сигнала активности

• Правило обучения, корректирующее связи

•

Множество простых процессоров

С каждым процессором (т.е. обрабатывающим элементом сети) связывается набор входящих связей, по которым к данному элементу поступают сиг­налы от других элементов сети, и набор исходящих связей, по которым сиг­налы данного элемента передаются другим элементам. Некоторые элементы предназначены для получения сигналов из внешней среды (и поэтому называются входными элементами), а некоторые — для вывода во внешнюю среду результатов вычислений (и поэтому такие элементы сети называются выходными элементами). Любая вычислительная машина имеет хотя бы одно уст­ройство ввода (например, клавиатуру), с помощью которого система получает данные из внешней среды, и устройство вывода (например, монитор), с помощью которого отображаются результаты вычислений. В случае программного моделирования реальных процессов на входные элементы обычно подаются уже предварительно подготовленные данные из некоторого файла данных, а не от непосредственно связанных с внешней средой датчиков.

Структура связей

Структура связей отражает то, как соединены элементы сети. В одной модели (т.е. для одного типа сетей) каждый элемент может быть связан со все­ми другими элементами сети, в другой модели элементы могут быть органи­зованы в некоторой упорядоченной по уровням (слоям) иерархии, где связи Допускаются только между элементами в смежных слоях, а в третьей — могут Допускаться обратные связи между смежными слоями или внутри одного слоя, или же допускаться посылка сигналов элементами самим себе. Возможности здесь практически бесконечны, но обычно для каждой конкретной модели сети указывается тип допустимых связей. Каждая связь определяется тремя параметрами: элементом, от которого исходит данная связь, элементом, к которому данная связь направлена, и числом (обычно действительным), указывающим весовой коэффициент (т.е. вес связи). Отрицательное значение веса соответствует подавлению активности соответствующего элемента, а положительное значение — усилению его активности. Абсолютное значение весового коэффициента характеризует силу связи.

Структура связей обычно представляется в виде весовой матрицы W, в которой каждый элемент w_ij представляет величину весового коэффи­циента для связи, идущей от элемента i к элементу j (обратите внимание на то, что во многих публикациях связи в весовых матрицах предполага­ются идущими от элемента j к элементу i, что, очевидно, следует учиты­вать при представлении матричных и векторных операций). Для описа­ния структуры связей может использоваться не одна, а несколько весо­вых матриц, если элементы сети оказываются сгруппированными в слои. На рис. 1.3 и 1.4 предлагаются примеры представления структуры связей в виде соответствующих матриц.

Матрица весов является памятью сети, хранящей информацию о том, как должна выполняться задача.

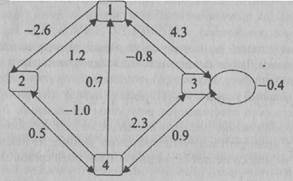
Рис. 1.3. Матрица, описывающая сетевые связи. В данном случае, например, вес связи элемента 3 (строка 3) с эле­ментом 1 (столбец 1) обозначается символом w₃₁ = -0.8

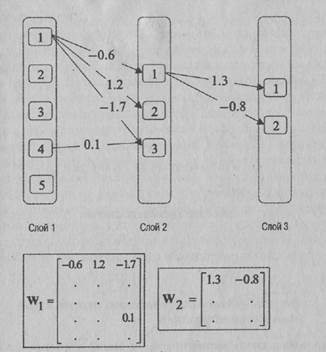
Рис. 1.4. Матрицы, описывающие сегевые связи. В данном случае для каждого слоя имеется своя отдельная матрица

Правило распространения сигналов в сети

В обычных компьютерных программах используются условия, выпол­нение которых определяет начало и конец различных процессов. То же са­мое верно и для нейронных сетей. Каждая конкретная модель сети предполагает наличие некоторого правила обновления состояния элементов сети (т.е. правила комбинирования входящих сигналов и вычисления исходящего сигнал) и посылки сигнала другим элементам- При этом в одних мо­делях моменты обновления элементов выбираются случайным образом, в других же моделях обновление некоторых групп элементов допускается только после обновления определенных групп других элементов.

Правило комбинирования входящих сигналов

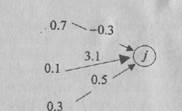
Довольно часто входящие сигналы элемента предполагается комби­нировать путем суммирования их взвешенных значений. Пример этого Метода суммирования показан на рис. 1.5, где netj обозначает результат

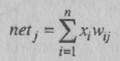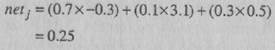или в векторном представлении

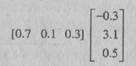
Рис. 1.5. Типичный метод суммирования сигналов, направ­ленных конкретному элементу

комбинирования ввода элемента j, x_f — выход элемента i, a n — число задействованных связей. Используются и другие формы комбинирования входящих сигналов, и другим часто встречающимся методом является рассмотрение квадрата разности между значением силы связи и значением передаваемого по связи сигнала с последующим суммированием таких разностей для всех входящих связей данного элемента.