Формулы преобразования произведения

; ;

.

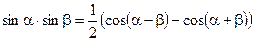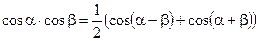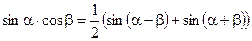Обратные тригонометрические функции

;

;

;

.

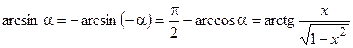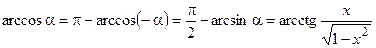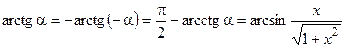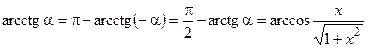Простейшие тригонометрические уравнения

1) ; ; .

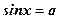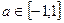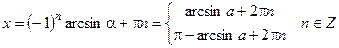Частные случаи: ; ;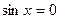

; ;

; .

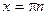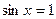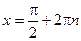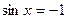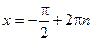2) ; ; .

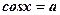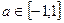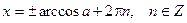Частные случаи: ; ;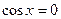

; ;

; .

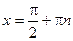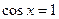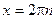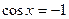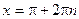3) , ; .

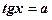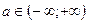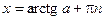4) ; ; .

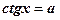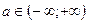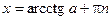RefM499.doc

8. Графики основных элементарных функций

Парабола

Гипербола

		y = ctg x		y = tg x

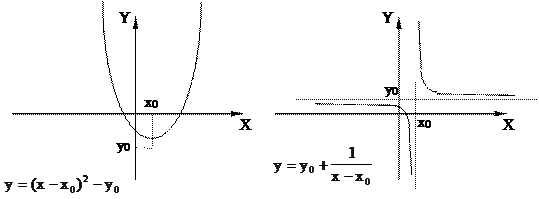ПЛАНИМЕТРИЯ

Треугольник

10.1.1. Основные соотношения

A,B,C – вершины aa,b,c – стороны a,b,g - углы

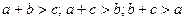- неравенства треугольника; ;

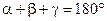теорема проекций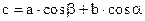

теорема синусов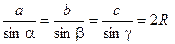

теорема косинусов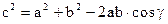

10.1.2. Замечательные линии и точки в теугольнике

m_a, m_b, m_c - медианы

h_a, h_b, h_c - высоты

l_a, l_b , l_c - биссектрисы

p - полупериметр,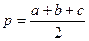

r - радиус вписанной окружности

R – радиус описанной окружности

; ;

; ;

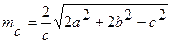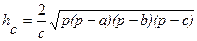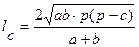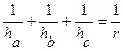10.1.3. Формулы площади треугольника

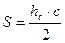
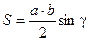
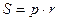
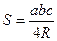
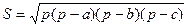(формула Герона)

Разбиение треугольника медианами

C     A D B

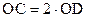
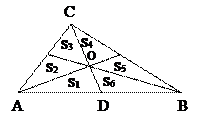
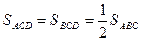
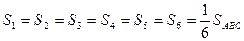
Свойство биссектрисы треугольника

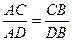
10.1.4. Прямоугольный треугольник

a b     c

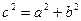(теорема Пифагора)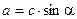

;

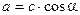
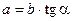
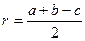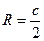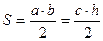
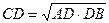C     A D B

;

или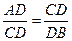

(CD - высота, опущенная на гипотенузу)

Подобия в прямоугольном треугольнике

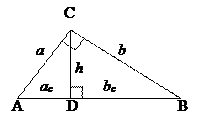
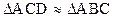
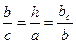
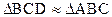
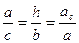
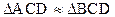
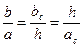
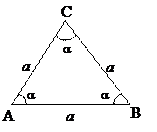
10.1.5. Правильный треугольник

p=3a (p - периметр)

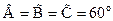
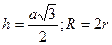
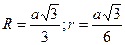
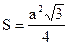
Четырехугольники

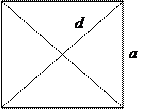10.2.1. Квадрат

S=a²

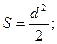
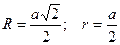
10.2.2. Прямоугольник

p=2(a+b) (p - периметр)

S=ab

10.2.3. Параллелограмм

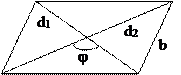p=2(a+b) (p - периметр)

a

a

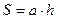
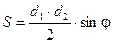
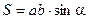
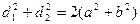
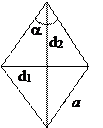10.2.4. Ромб

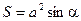
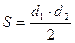
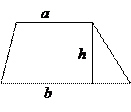10.2.6. Трапеция

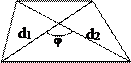
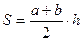
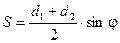
Свойства трапеции

1. Во всякой трапеции середины

оснований К, М лежат на прямой,

проходящей через точку пересечения

диагоналей О и точку пересечения

продолжений боковых сторон.

	K

2. Средняя линия трапеции параллельна

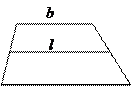основаниям и равна их полусумме.

a

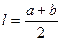
Окружность и круг.

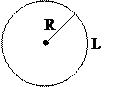Длина окружности

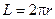
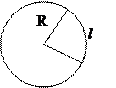длина дуги окружности

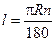
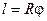
(n - величина дуги в градусах, j - величина дуги в радианах).

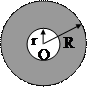Площадь круга

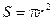
площадь кольца

.

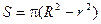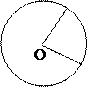Площадь сектора

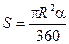; (a - величина дуги в градусах)

Свойства окружности

1) касательная и радиус, проведенный в точку касания,

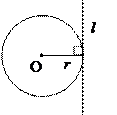перпендикулярны: r ^ l

2) отрезки касательных, проведенные к окружности

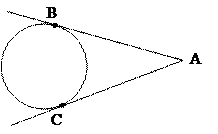из точки, лежащей вне ее, равны, т.е.

AB = AC

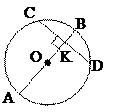3) диаметр, перпендикулярный хорде, делит ее пополам; диаметр, проходящий через середину хорды, перпендикулярен ей.

(AB) ^ (CD) Û CK = KD

4) квадрат длины касательной равен произведению длины

секущей на ее внешнюю часть:

AB² =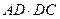

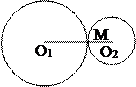5) центры касающихся окружностей О₁, О₂ и точка их касания М лежат на одной прямой.

C

6) в четырехугольник можно вписать окружность тогда и

только тогда, когда суммы длин противоположных

сторон равны, т.е.:

AB + BC = AB + CD

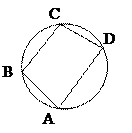7) около четырехугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна

180⁰, т.е.:

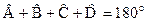
Следствия из свойства 7):

- из всех параллелограммов только около прямоугольника можно описать окружность;

- около трапеции можно описать окружность тогда и только тогда, когда она равнобокая;

8) центральный угол измеряется градусной мерой дуги, на

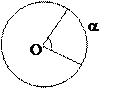которую он опирается:

ÐО = Èa

9) величина вписанного угла 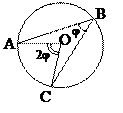в два раза меньше центрального

угла, опирающегося на эту же дугу

ÐAOC = 2ÐABC

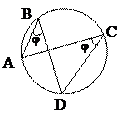10) вписанные углы, опирающиеся на одну и ту же дугу, имеют одинаковую величину

ÐABD = ÐACD

СТЕРЕОМЕТРИЯ

11.1. Куб

Объем

V = a³

Площадь поверхности

S = 6a²

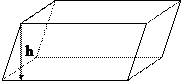11.2. Параллелепипед

Объем

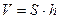
(S - площадь основания, h - высота)