Определение. Матрицу , получаемую из матрицы А заменой строк и столбцов друг на друга, называют транспонированной

Например, если 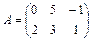, то .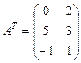

1. Любую матрицу можно умножить на любое действительное число : .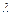

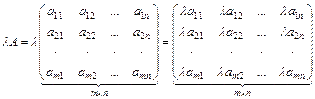2. Матрицы одной и той же размерности можно складывать (вычитать):

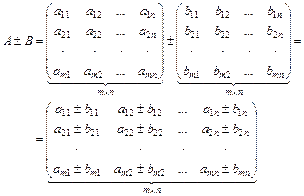
3. Матрицу А можно умножать на матрицу В только, если число столбцов матрицы А равно числу строк матрицы В:

,

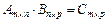причем элементы матрицы С находятся по правилу:

,

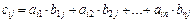то есть элементы i–ой строки матрицы А умножаются на соответствующие элементы j–го столбца матрицы В и полученные произведения складываются.

§ 2. Определители и их вычисление.

Каждой квадратной матрице по определенному правилу ставится в соответствие число, называемое определителем.

1.Правило вычисления определителя 2-го порядка:

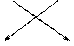
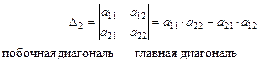
2.Правило вычисления определителя 3-го порядка – правило треугольников:

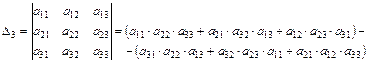
Правило разложения определителя по элементам 1-й строки:

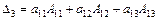, где алгебраические дополнения 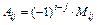, а минор 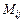– определитель, получающийся из данного путем вычеркивания i-ой строки и j-го столбца.

Таким образом,

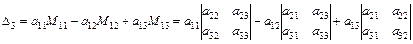
Аналогично определитель можно раскладывать по элементам любой строки или столбца.

3.Правило вычисления определителя n–го порядка. Определители n–го порядка вычисляются также разложением по элементам любой строки или столбца.

Таким образом,

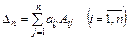– разложение определителя по элементам i–ой строки

или

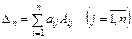– разложение определителя по элементам j–го столбца

§ 3. Решение систем линейных уравнений

1. Формулы Крамера для решения систем трех линейных уравнений с тремя неизвестными:

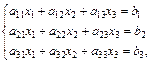
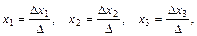
где

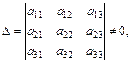
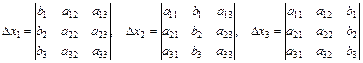
2. Метод Гаусса.

Сущность метода состоит в том, что посредством последовательных исключений неизвестных, данная система преобразуется в систему ей эквивалентную. Последовательное исключение неизвестных осуществляется с помощью элементарных преобразований системы:

а) перестановок двух любых уравнений;

б) умножений обеих частей одного из уравнений на любое, отличное от нуля число;

в) прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.

Заметим, что удобно работать не с самими уравнениями системы, а с ее расширенной матрицей.