Решение ДУ – любая функция, которая, будучи подставлена в исходную запись уравнение, обращает его в тождество!
Прочти, реши и опять прочти!..
Настоящее методическое пособие предназначено помочь студентам в освоении теоретических вопросов предмета «Дифференциальные уравнения» путём использования подробно решённых задач и примеров.
Одновременно, пособие должно помочь наиболее мотивированным студентам развивать навыки самостоятельной работы, что очень важно при подготовке инженера любой специальности.
Тем, кто захочет воспользоваться возможностью показать себя постоянно и эффективно работающим, привлечь к себе внимание преподавателей и научных руководителей, приобрести авторитет среди своих товарищей, пособие тоже окажет помощь.
Рассмотренные и доступные с самого начала семестра материалы помогут качественно готовиться и к лекциям, и практическим занятиям, и к различным контрольным испытаниям.
СОДЕРЖАНИЕ:
| № | Тема занятия: | Стр. |
| 1. | Основные понятия. Теорема о существовании и единственности решения ДУ 1-го порядка. Уравнение 1-го порядка с разделяющимися переменными. | |
| 2. | Уравнения первого порядка с разделяющимися переменными. Систематизация и закрепление знаний. | |
| 3. | Однородные функции и однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному ДУ 1-го порядка. Выдача части-1 БДЗ. | |
| 4. | Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли. | |
| 5. | Уравнения в полных дифференциалах. | |
| 6. | Уравнения 1-го порядка, не разрешённые относительно производной. | |
| 7. | Повторение: все типы уравнений 1-го порядка. Обзорные упражнения: определение типа дифференциального уравнения и обсуждение общего алгоритма решения. Систематизация знаний. Подготовка к контрольной работе. | |
| 8. | Уравнения 1-го порядка. Контрольная работа №1.Приём части-1 БДЗ. Выдача части-2 БДЗ. | |
| 9. | Уравнения высших порядков. Уравнения, допускающие понижение порядка. | |
| 10. | Линейные ДУ n-го порядка. Линейная зависимость решений линейного уравнения. Линейное однородное уравнение. | |
| 11. | Линейные неоднородные уравнения с постоянными коэффициентами. Решение методами: «вариации произвольных постоянных» и «неопределенных множителей». | |
| 12. | Краевые задачи для линейных дифференциальных уравнений. Повторение: решение линейных ДУ 2-го и 3-го порядков. Систематизация знаний. Подготовка к контрольной работе. | |
| 13. | Уравнения n-го порядка. Контрольная работа №2. Прием части-2 БДЗ. Выдача части-3 БДЗ. | |
| 14. | Системы дифференциальных уравнений первого порядка. Сведение системы ДУ к одному уравнению высшего порядка. | |
| 15. | Системы линейных однородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами: общее и частное решения. | |
| 16. | Системы линейных неоднородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами. Правая часть: специальная и произвольная. Самостоятельная работа – 40 мин. Приём части-3 БДЗ. | |
| 17. | Повторение и систематизация материала. Подготовка к экзамену. |
•◄●►•
Замечание: если в рассматриваемом Задании пример имеет номер 3-9, это значит, что цифра 3 указывает порядковый номер примера в этом Задании, а цифра 9 указывает номер примера из Задачника, указанного в Семестровом плане студентов.
ЗАНЯТИЕ 1. Основные понятия. Теорема существования и единственности ДУ 1-го порядка. Уравнения первого порядка с разделяющимися переменными.
☺ ☻ ☺
Основные понятия:
Дифференциальным уравнением (ДУ) называют равенство, содержащее независимые переменные, искомую функцию и её производные (или дифференциалы).
Решить ДУ – значит найти все его решения!
Решение ДУ – любая функция, которая, будучи подставлена в исходную запись уравнение, обращает его в тождество!
••• ≡•••
Пример 1–1: Показать, что при любом действительном значении параметра 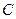 заданная функция
заданная функция 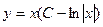 является решением ДУ:
является решением ДУ: 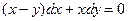 . (1)
. (1)
Решение:
1). Разделим уравнение на 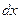 . Получаем уравнение в виде:
. Получаем уравнение в виде: 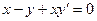 . (2)
. (2)
2). Для нахождения производной заданной функции вспомним: 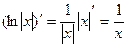 , так как имеем:
, так как имеем: 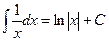 - табличный интеграл! Тогда:
- табличный интеграл! Тогда: 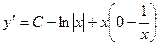 =
= 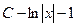 .
.
3). Подставим заданную функцию 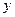 и ее производную
и ее производную 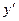 в уравнение (2), которое равносильно исходному уравнению (1):
в уравнение (2), которое равносильно исходному уравнению (1): 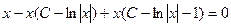 → тождество.
→ тождество.
4). Это значит, что заданная функция является решением заданного уравнения.
Ответ: заданная функция является решением заданного уравнения.
Пример 2–4: В заданном семействе: 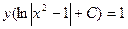 выделить уравнение кривой, удовлетворяющей приведенному начальному условию:
выделить уравнение кривой, удовлетворяющей приведенному начальному условию: 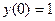 .
.
Решение:
1). Выделить из семейства кривых кривую, которая проходит через точку (0,1) – это значит вычислить значение произвольной постоянной 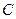 , при условии, что
, при условии, что 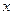 =0,
=0, 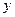 =1.
=1.
2). Подставим 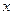 =0,
=0, 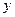 =1 в выражение семейства:
=1 в выражение семейства: 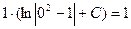 , откуда
, откуда 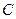 =1.
=1.
3). Тогда уравнение кривой семейства, проходящей через точку (0,1): 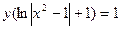 .
.
Ответ: уравнение кривой: 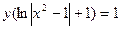 .
.
Пример 3–9: Составить дифференциальное уравнение семейства парабол: 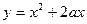 . (1)
. (1)
Решение:
1). Преобразуем выражение семейства (известная операция выделения полного квадрата): 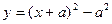 . При непрерывном изменении параметра
. При непрерывном изменении параметра 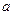 ось параболы
ось параболы 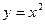 смещается влево при значении параметра
смещается влево при значении параметра 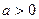 , вправо при значении
, вправо при значении 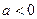 ; одновременно вершина параболы движется по параболе
; одновременно вершина параболы движется по параболе 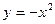 .
.
2). Вычислим производную 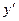 для заданного семейства:
для заданного семейства: 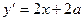 . (2)
. (2)
3). Для получения дифференциального уравнения нужно исключить параметр 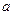 из выражения (1) или из выражения (2):
из выражения (1) или из выражения (2):
а) умножив выражение (2) на 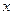 , получим уравнение
, получим уравнение 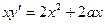 =[учтём (1)] =
=[учтём (1)] = 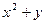 ;
;
б) получено дифференциальное уравнение: 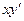 =
= 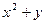 .
.
Ответ: ДУ для семейства парабол 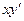 =
= 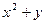 .
.
Пример 4–16: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: 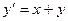 .
.
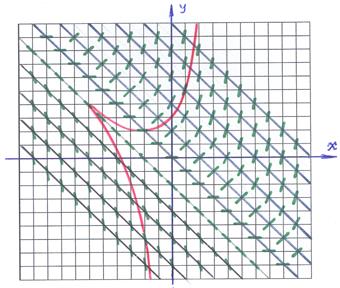 Решение:
Решение:
1). Уравнение изоклин для заданного дифференциального уравнения получается из исходного уравнения приравниванием 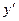 =
= 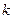 . В нашем случае каждая изоклина – это прямая:
. В нашем случае каждая изоклина – это прямая: 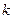 =
= 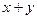 . На рисунке изоклины выделены «синим» цветом. На каждой изоклине черточка («зеленая») отражает конкретное значение
. На рисунке изоклины выделены «синим» цветом. На каждой изоклине черточка («зеленая») отражает конкретное значение 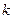 , определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.
, определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.
2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «красным» цветом), то есть «решение» заданного ДУ.
Ответ: интегральная кривая представлена на рисунке.
Пример 5–26: Решить дифференциальное уравнение: 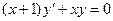 . (1)
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) не может иметь решения в виде 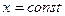 , в частности в виде функции
, в частности в виде функции 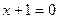 . Это значит, что дифференциал
. Это значит, что дифференциал 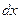 не может быть равным 0. В то же время, функция
не может быть равным 0. В то же время, функция 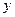 =0 есть решение уравнения (1).
=0 есть решение уравнения (1).
2). Умножим исходное уравнение (1) на дифференциал 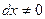 . Уравнение (1) перепишем в дифференциальной форме:
. Уравнение (1) перепишем в дифференциальной форме: 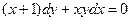 . (2)
. (2)
3). Нетрудно заметить, что уравнение (2) есть уравнение с разделяющимися переменными. Так как решение 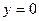 уже учтено, теперь примем, что
уже учтено, теперь примем, что 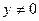 и перепишем уравнение (2) в виде:
и перепишем уравнение (2) в виде: 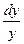 +
+ 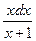 =0. (3)
=0. (3)
4). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (3). При получении общего решения уравнения (3) применим два принципиально разных способа использования произвольной постоянной величины:
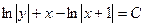 →
→ 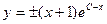 или
или 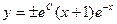 . (4)
. (4)
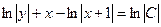 →
→ 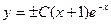 или
или 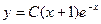 . (5)
. (5)
Замечания: 1. При получении выражений (4) и (5) принципиальным было применение условия y≠0. При получении записи (5) также необходимо потребовать выполнения условия C≠0!..
2. Использование записи (5) удобнее в случае решения задачи Коши: вычисление постоянной C совсем просто, при использовании (4) пришлось бы применять логарифмы!..Если общее решение уравнения воспринимать как совокупность кривых, то записи эквиваленты!..
Ответ: общее решение ДУ 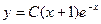 ; хотя при получении общего решения произвольная постоянная величина
; хотя при получении общего решения произвольная постоянная величина 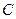 не должна принимать значение 0, формально из него можно получить решение исходного уравнения
не должна принимать значение 0, формально из него можно получить решение исходного уравнения 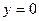 при значении
при значении 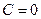 .
.
Пример 6–31: Решить дифференциальное уравнение: 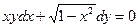 . (1)
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) имеет решения в виде функций: 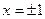 – прямые, параллельные оси
– прямые, параллельные оси 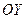 , и
, и 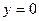 , то есть ось
, то есть ось 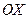 .
.
2). Теперь воспользуемся тем, что переменные в уравнении разделяются. Так как решения 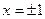 и
и 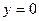 учтены, примем теперь
учтены, примем теперь 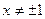 и
и 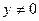 , и запишем уравнение в виде:
, и запишем уравнение в виде:
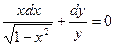 . (2)
. (2)
3). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (2). Получаем общее решение уравнения (2):
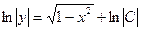 →
→ 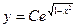 . (3)
. (3)
Ответ: общее решение ДУ 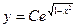 ; в данном случае решение исходного уравнения
; в данном случае решение исходного уравнения 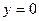 можно получать из общего при значении
можно получать из общего при значении 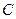 =0; решения
=0; решения 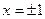 также формально можно получать из общего решения.
также формально можно получать из общего решения.
Пример 7–41: Решить дифференциальное уравнение: 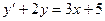 . (1)
. (1)
Решение:
1). Преобразуем заданное уравнение к виду: 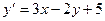 =
= 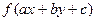 . Известно, что такое уравнение легко приводится к уравнению с разделяющимися переменными!
. Известно, что такое уравнение легко приводится к уравнению с разделяющимися переменными!
2). Примем 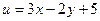 и вычислим производную
и вычислим производную 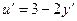 , то есть
, то есть 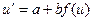 . В нашем случае получаем
. В нашем случае получаем 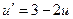 , что есть уравнение с разделяющимися переменными!
, что есть уравнение с разделяющимися переменными!
3). Уравнение 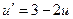 имеет решение в виде функции:
имеет решение в виде функции: 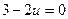 . Учитывая обозначение
. Учитывая обозначение 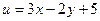 , запишем решение
, запишем решение 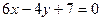 – прямая линия.
– прямая линия.
Замечание: Увидеть решение 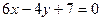 непосредственно из исходного уравнения было бы совсем непросто!
непосредственно из исходного уравнения было бы совсем непросто!
4). Пусть теперь 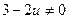 . Запишем уравнение
. Запишем уравнение 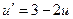 в виде:
в виде: 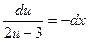 , или (для удобства!) в виде:
, или (для удобства!) в виде: 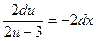 . (2)
. (2)
5). Интегрирование уравнения (2) не составит труда, даже на начальном этапе освоения неопределённого интеграла 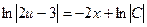 →
→ 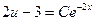 . (3)
. (3)
Ответ: общее решение ДУ 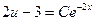 ; в данном случае решение
; в данном случае решение 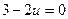 можно получить формально из общего при значении
можно получить формально из общего при значении 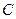 =0; запишем общее решение и в виде
=0; запишем общее решение и в виде 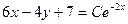 , из которого решение
, из которого решение 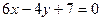 получается из общего при значении
получается из общего при значении 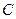 =0.
=0.
Пример 8–43: Решить дифференциальное уравнение: 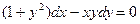 ,
, 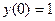 . (1)
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) имеет решение: 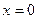 – ось
– ось 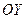 .
.
2). Переменные в уравнении разделяются. Так как решение 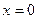 уже учтено, примем теперь
уже учтено, примем теперь 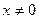 , и запишем уравнение в виде:
, и запишем уравнение в виде: 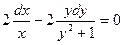 . (2)
. (2)
3). Интегрирование уравнения (2) не составит труда, даже на начальном этапе освоения неопределённого интеграла 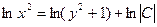 →
→ 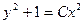 . (3)
. (3)
4). Используя начальные условия 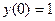 , вычисляем:
, вычисляем: 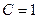 и получаем частное решение уравнения:
и получаем частное решение уравнения: 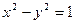 – гипербола, её график включает две ветви. Начальные условия выделяют правую ветвь гиперболы!
– гипербола, её график включает две ветви. Начальные условия выделяют правую ветвь гиперболы!
Ответ: 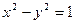 – частное решение ДУ: правая ветвь гиперболы.
– частное решение ДУ: правая ветвь гиперболы.
Пример 16–167: Найти уравнение кривой линии, проходящей через точку 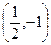 , если длина отрезка полуоси абсцисс, отсекаемого её касательной, равна квадрату абсциссы точки касания.
, если длина отрезка полуоси абсцисс, отсекаемого её касательной, равна квадрату абсциссы точки касания.
Решение:
В Примере 1–18 Главы 1 пособия получено выражения: OT= 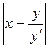 – длина отрезка полуоси абсцисс, отсекаемого её касательной; абсциссу точки касания обозначим D=
– длина отрезка полуоси абсцисс, отсекаемого её касательной; абсциссу точки касания обозначим D= 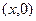 .
.
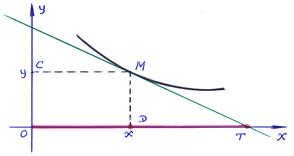 Согласно условию задачи и в соответствии с принятыми обозначениями необходимо рассмотреть два случая:
Согласно условию задачи и в соответствии с принятыми обозначениями необходимо рассмотреть два случая:
▪ Случай-1: 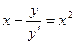 ; (1)
; (1)
▪ Случай-2: 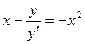 . (2)
. (2)
Случай-1.
1). Запишем дифференциальное уравнение (1) в виде: 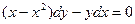 – уравнение с разделяющимися переменными, обозначим его
– уравнение с разделяющимися переменными, обозначим его 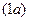 .
.
2). Из записи 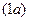 нетрудно выделить решения:
нетрудно выделить решения: 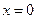 – ось
– ось 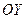 ,
, 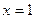 – прямая, параллельная оси
– прямая, параллельная оси 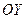 и
и 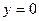 – ось
– ось 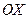 . Эти решения не отражают существа поставленной геометрической задачи.
. Эти решения не отражают существа поставленной геометрической задачи.
3). Пусть теперь 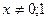 и
и 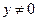 . Перепишем уравнение
. Перепишем уравнение 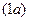 в виде
в виде 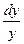 =
= 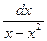 – переменные разделились. Интегрируем уравнение:
– переменные разделились. Интегрируем уравнение: 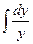 –
– 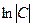 =
= 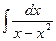 =
= 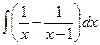 . Используя табличные интегралы и исключая логарифмы, можем записать общее решение:
. Используя табличные интегралы и исключая логарифмы, можем записать общее решение:
 =
= 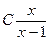 , или
, или 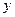 =
= 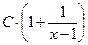 . (3)
. (3)
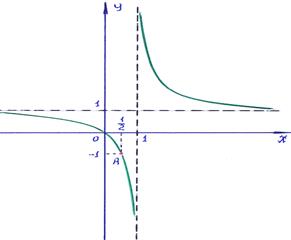
4). Из записи общего решение дифференциального уравнения следует, что это семейство гипербол.
Для иллюстрации присвоим произвольной величине 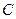 значение 1. Известно, что график функции
значение 1. Известно, что график функции 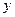 =
= 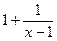 может быть получен, если к простейшей гиперболе
может быть получен, если к простейшей гиперболе 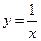 применить преобразования:
применить преобразования:
— Сместить график вправо на 1, лучше сместить ось  на 1 влево.
на 1 влево.
— Сместить график вверх на 1, лучше сместить ось  на 1 вниз.
на 1 вниз.
Учёт параметра 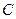 в записи (3) может быть отмечен возможными действиями: сжатие-растяжение вдоль оси
в записи (3) может быть отмечен возможными действиями: сжатие-растяжение вдоль оси 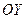 , вращение вокруг оси
, вращение вокруг оси 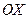 и движение вверх-вниз.
и движение вверх-вниз.
Так как по условию задачи кривая должна проходить через точку 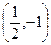 , то используя выражение общего решения (3), получаем значение
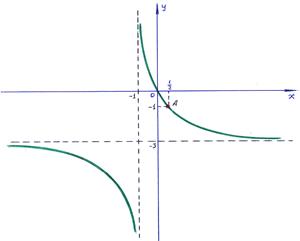
, то используя выражение общего решения (3), получаем значение 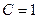 . Именно для этого случая применён рисунок. Учитывая условие задачи, заметим, что решением является ветвь гиперболы, проходящая через точку
. Именно для этого случая применён рисунок. Учитывая условие задачи, заметим, что решением является ветвь гиперболы, проходящая через точку 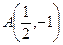 .
.
Случай-2.
1). Запишем дифференциальное уравнение (2) в виде: 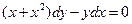 – уравнение с разделяющимися переменными, обозначим его
– уравнение с разделяющимися переменными, обозначим его 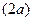 .
.
 2). Из записи
2). Из записи 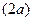 нетрудно выделить решения:
нетрудно выделить решения:  – ось
– ось  ,
, 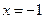 – прямая, параллельная оси
– прямая, параллельная оси 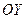 и
и 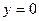 – ось
– ось 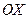 . Эти решения не отражают существа поставленной геометрической задачи.
. Эти решения не отражают существа поставленной геометрической задачи.
3). Пусть теперь 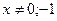 и
и 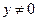 . Перепишем уравнение
. Перепишем уравнение 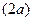 в виде
в виде 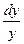 =
= 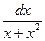 – переменные разделились. Интегрируем уравнение:
– переменные разделились. Интегрируем уравнение: 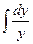 –
– 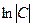 =
= 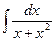 =
= 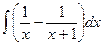 . Используя табличные интегралы и исключая логарифмы, можем записать общее решение:
. Используя табличные интегралы и исключая логарифмы, можем записать общее решение:
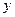 =
= 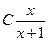 , или
, или 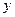 =
= 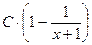 . (4)
. (4)
4). Из записи общего решение дифференциального уравнения следует, что это семейство гипербол.
Для иллюстрации присвоим произвольной величине 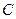 значение –3. Известно, что график функции
значение –3. Известно, что график функции 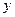 =
= 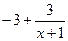 может быть получен, если к простейшей гиперболе
может быть получен, если к простейшей гиперболе 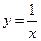 применить преобразования:
применить преобразования:
— Сместить график влево на 1, лучше сместить ось 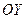 на 1 вправо.
на 1 вправо.
— Сместить график вниз на 3, лучше сместить ось 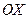 на 3 вверх.
на 3 вверх.
Учёт параметра 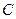 в записи (4) может быть отмечен возможными действиями: сжатие-растяжение вдоль оси
в записи (4) может быть отмечен возможными действиями: сжатие-растяжение вдоль оси 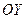 , вращение вокруг оси
, вращение вокруг оси 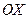 и движение вверх-вниз.
и движение вверх-вниз.
Так как по условию задачи кривая должна проходить через точку 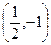 , то используя выражение общего решения (4), получаем значение
, то используя выражение общего решения (4), получаем значение 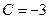 . Именно для этого случая применён рисунок. Учитывая условие задачи, заметим, что решением является ветвь гиперболы, проходящая через точку
. Именно для этого случая применён рисунок. Учитывая условие задачи, заметим, что решением является ветвь гиперболы, проходящая через точку 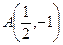 .
.
Ответ: Случай-1: 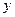 =
= 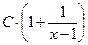 – общее решение и частное:
– общее решение и частное: 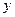 =
= 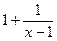 .
.
Случай-2: 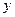 =
= 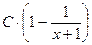 – общее решение и частное:
– общее решение и частное: 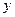 =
= 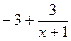 .
.
☻
Вопросы для самопроверки:
1. Какое уравнение называют дифференциальным?
2. Как определить порядок ДУ?
3. Что значит - решить дифференциальное уравнение?
4. Что такое решение ДУ, частное решение ДУ?
5. Что такое общее решение ДУ?
6. Что значит решить Задачу Коши?
7. Что такое семейство кривых?
8. Как построить уравнение, решением которого является заданное семейство кривых?
9. Каковы стандартные формы ДУ с разделяющимися переменными и их решение?
Задачи для самоподготовки:
Пример C1–1: В заданном семействе: 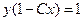 выделить уравнение кривой, удовлетворяющей приведенному начальному условию:
выделить уравнение кривой, удовлетворяющей приведенному начальному условию: 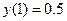 .
.
Ответ: 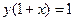 .
.
Пример C1–2: Решить дифференциальное уравнение: 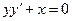 .
.
Ответ:y2 +x2 = C.
Пример C1–3: Решить дифференциальное уравнение: y′ 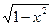 = 1+ y2.
= 1+ y2.
Ответ: 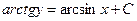 , также
, также 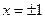 .
.
Пример C1–4: Решить дифференциальное уравнение: y′ = ex+y.
Ответ:ex +e–y = C.
Пример C1–5: Решить дифференциальное уравнение: 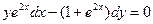 .
.
Ответ: 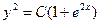 .
.
Пример C1–6: Найти уравнение кривой, проходящей через точку (1,2), если её подкасательная вдвое больше абсциссы точки касания.
Ответ: 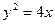 и
и 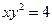 .
.
< * * * * * >
