Законы распределения. Основные характеристики случайных величин
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной случайной величиной (ДСВ) называют такую величину, множество значений которой либо конечное, либо бесконечное, но счетное.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Его можно задать таблично, аналитически (формулой) или графически.
Простейшей формой задания закона распределения дискретной случайной величины Х является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
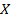 | 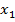 | 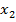 | … | 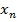 | |
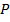 | 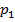 | 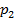 | … | 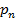 | 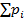 i i |
Эта таблица называется рядом распределения ДСВ.
О каждой случайной величине необходимо прежде всего знать ее среднее значение 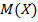 , около которого группируются возможные значения случайной величины, а также число
, около которого группируются возможные значения случайной величины, а также число 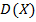 , характеризующее степень разбросанности этих значений относительно среднего.
, характеризующее степень разбросанности этих значений относительно среднего.
Определение: Математическим ожиданием ДСВ 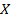 , заданной законом распределения:
, заданной законом распределения:
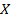 | 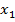 | 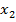 | … | 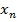 |
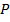 | 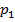 | 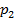 | … | 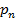 |
называется число 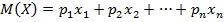 .
.
Заметим, что математическое ожидание для данной ДСВ Х есть величина постоянная.
Дисперсией случайной величины 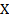 называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
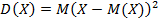 .
.
Для вычисления 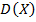 удобнее пользоваться следующей формулой, которая выводится на основании свойств математического ожидания:
удобнее пользоваться следующей формулой, которая выводится на основании свойств математического ожидания:
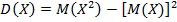 .
.
Средним квадратическим отклонением случайной величины 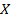 называется корень квадратный из ее дисперсии:
называется корень квадратный из ее дисперсии:
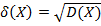 .
.
Примеры решения задач
Пример 1. Приживаемость саженцев яблонь составляет 80%. Наудачу выбирают 5 саженцев. Составить закон распределения числа прижившихся саженцев, построить многоугольник распределения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа прижившихся саженцев.
Решение:
Вероятность приживаемости яблони равна 0,8.
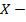 случайная величина числа прижившихся яблонь из пяти саженцев. Возможные значения случайной величины:
случайная величина числа прижившихся яблонь из пяти саженцев. Возможные значения случайной величины: 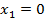 - ни один саженец не прижился;
- ни один саженец не прижился;
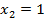 - один саженец прижился;
- один саженец прижился;
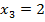 - два саженца прижились;
- два саженца прижились;
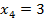 - три саженца прижились;
- три саженца прижились;
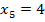 - четыре саженца прижились;
- четыре саженца прижились;
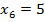 - пять саженцев прижились.
- пять саженцев прижились.
Вероятности этих значений вычислим по формуле Бернулли ( 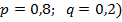 :
:
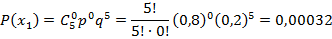
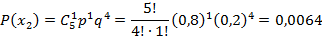
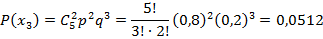
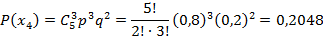
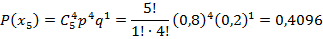
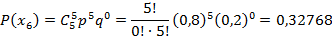
Таким образом, закон распределения случайной величины:
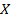 | ||||||
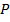 | 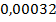 | 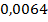 | 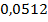 | 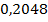 | 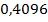 | 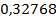 |
Проверка: 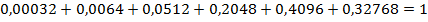
Построим многоугольник распределения:
 Найдем числовые характеристики случайной величины, для этого составим таблицу:
Найдем числовые характеристики случайной величины, для этого составим таблицу:
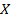 | ||||||
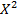 | ||||||
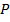 | 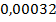 | 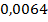 | 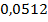 | 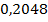 | 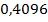 | 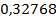 |
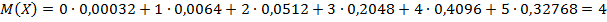
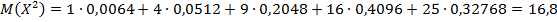
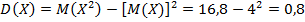
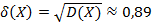 .
.
