Поведение системы спинов в постоянном и переменном магнитном поле

В полученном нами элементарном квантовомеханическом условии резонанса (9) отсутствует постоянная планка 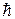. Это указывает на возможность классической интерпретации явления, при которой ряд характерных особенностей магнитного резонанса удаётся изложить гораздо проще и нагляднее. Поэтому классическая теория резонанса наряду с квантовой получила широкое распространение.

В классической механике доказывается [3], что изменение момента количества движения должно равняться моменту действующих сил. Применительно к спину с моментом 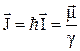, находящемуся в постоянном магнитном поле 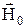, это даёт

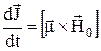(25)

или

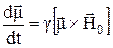. (25а)

Поскольку векторное произведение 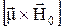есть вектор, направленный перпендикулярно плоскост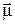и и 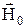, вектор 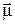будет описывать конус вокруг 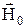с постоянным углом θ при вершине. Этот результат можно получить более строго, расписав уравнение (25а) в проекциях по осям:

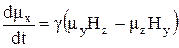. (26)

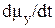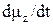(Выражения для и аналогичны и отличаются только циклической перестановкой координатных индексов). Если ось z выбрать параллельно 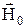, то H_z=H₀ и H_x=H_y=0. Поэтому из (26) и аналогичных выражений для 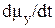и 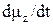получим

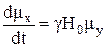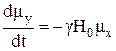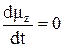; ; . (27)

Для 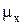отсюда можно найти

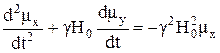, (28)

или

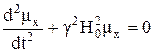. (28а)

Следовательно, 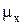совершает гармонические колебания с частотой 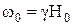по закону 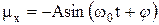, где А и φ – постоянные интегрирования. Аналогично можно получить для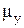

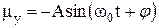. (29)

Отсюда следует, что проекция 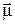на плоскость xz, т.е. 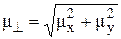, остаётся постоянной по величине и вращается с частотой ω₀ против часовой стрелки (если смотреть по направлению вектора 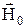). Таким образом, с учётом условия 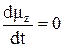, означающего, что 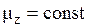, мы видим, что вектор 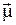вращается против часовой стрелки с так называемой ларморовской частотой 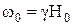, совпадающей с (9).

Пусть теперь кроме постоянного поля 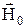имеется ещё и переменное поле, действующее в плоскости, перпендикулярной H₀: 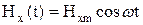. Это поле может быть представлено как состоящее из двух компонент, вращающихся с частотой ω в разные стороны. Вблизи резонанса (ω≈w₀) с магнитным полем будет взаимодействовать только компонента магнитного поля, вращающаяся в ту же сторону, что и :

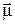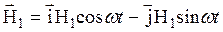, (30)

в то время как действием компоненты, вращающейся в противоположную сторону, можно пренебречь. При этом суммарное поле

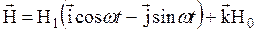, (31)

где 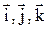– орты координатных осей. Для выяснения действия поля H₁(t) удобно ввести систему координат, вращающуюся с частотой w в ту же сторону, что и H₁(t) вокруг оси z. В ней вектор 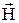будет покоиться. Из классической механики известно, что скорость изменения вектора во вращающейся системе координат 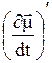связана со скоростью изменения этого же вектора в лабораторной системе координат 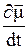соотношением (вектор угловой скорости направлен в сторону отрицательного направления оси z)

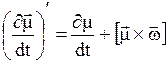. (32)

Если направить ось х^’ вращающейся системы координат (ВСК) вдоль 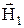, то вместо (30) мы будем иметь 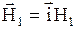, и, имея в виду (25а), можно записать:

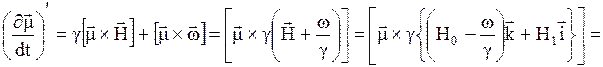
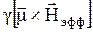, (33)

где

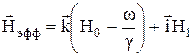. (34)

Как видно из сравнения (33) с выражением (25а), во вращающейся системе координат магнитный момент движется так, как если бы на него действовало эффективное магнитное поле 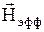, т.е. он прецессирует вокруг 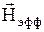с угловой частотой 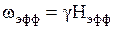(рис. 2).

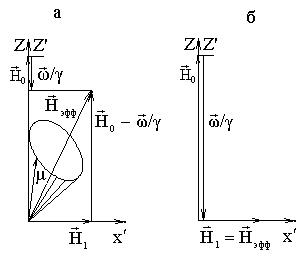
Рис. 2. Движение спина в постоянном и переменном магнитном поле: а – ,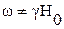

б –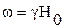

Если частота переменного поля равна ларморовской частоте, то, поскольку вектор 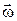антипараллелен полю 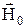(см. рис. 2), 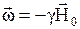и 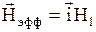. Поэтому при условии точного резонанса вектор магнитного момента прецессирует вокруг оси х^’ вращающейся системы координат с частотой 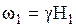. Заметим, что эта частота обычно много меньше 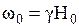, так как H₁ имеет порядок единиц эрстед, тогда как H₀~10⁴ Э.

Поведение вектора суммарного магнитного момента образца, содержащего большое число спинов 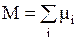несколько отличается от поведения индивидуального спина 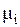. Если действует только постоянное поле H₀, то нетрудно понять, суммируя проекции спинов на ось z и на плоскость xy, что величина M_z, пропорциональная разнице числа спинов, ориентированных «по» и «против» поля 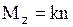, как и M_z, остаётся постоянной, в то время как 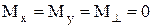в отличие от соответствующих величин для отдельного спина. Это видно из того, что фазы прецессии отдельных спинов произвольны, следовательно, при большом числе спинов в любой момент времени для любого спина, имеющего определённое направление проекции в плоскости xy, найдётся другой спин, имеющий прямо противоположное направление проекции, лежащей в той же плоскости.