Отражение и преломление на границе двух диэлектриков

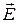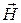При распространении света в изотропной среде отсутствуют причны изменения направления векторов или , т.е. поляризации. Это существенно облегчает расчет электромагнитных полей, так как можно ввести такую систему координат, чтобы только одна компонента поля была отлична от нуля 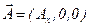и анализ проводится так, как будто 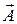является скаляром. Такой подход лежит в основе скалярной теории распространения электромагнитного поля.

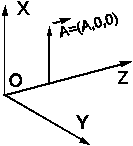рис. 9.1

В случае нарушения изотропии, направления вектора 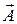может меняться и анализа одной компоненты 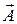уже недостаточно. Необходимо отслеживать все компоненты, а это и есть векторная модель распространения электромагнитного поля.

рис. 9.2

Простейшим случаем нарушения изотропии пространства, появления анизотропии, является наклонное падение света на границу раздела двух сред. Если определить плоскость падения как плоскость, проходящую через луч 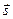и нормаль 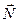к поверхности, то из рисунка (рис 9.2) видно, что условия взаимодействия луча и поверхности будут различными для разных ориентаций вектора 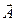относительно плоскости падения. Если же луч падает на поверхность по нормали, то изотропия относительно луча не нарушается. Таким образом, преломление и отражение при наклонном падении должно изменять так называемое состояние поляризации световой волны.

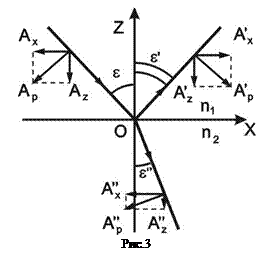Определим соотношения между напряженностями электромагнитных волн и их интенсивностей для падающей, преломленной и отраженной волнами при произвольном падении луча на границу раздела двух сред. Будем считать, что плоскость падения лежит в плоскости 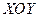. Кроме того, будем помечать все параметры отраженной волны одним штрихом ( ‘ ), а параметры преломленной волны двумя штрихами ( “ ) и компоненты полей в плоскости падения индексом 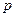, а в плоскости, перпендикулярной ей - 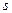и полагать, что угол падения исходной волны меньше угла полного внутреннего отражения (т.е. преломленная волна существует) (рис 9.3).

Для получения искомых соотношений следует воспользоваться известных из физики граничных условий, которые заключаются в том, что проекции векторов электрической и магнитной напряженности по обе стороны раздела должны быть одинаковы, в противном случае там должны бы появиться токи, но этого не должно быть, поскольку среды диэлектрические.

Обозначив за 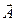вектор амплитуды электрического или магнитного поля (это пока несущественно, так как поведение 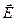или 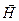в световой волне совершенно идентично), запишем проекции 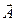на линию раздела - ось 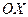. Из рисунка (9.3) следует, что для составляющих векторов, лежащих в плоскости падения будет

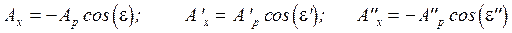. (9.1)

Составляющие, которые перпендикулярны плоскости падения, параллельны плоскости раздела и их проекции равны их значениям.

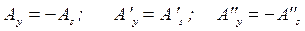. (9.2)

Так как в подпространстве с показателем преломления 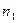распространяется две волны - падающая и отраженная, а в другом - только преломленная, то граничные условия запишутся как

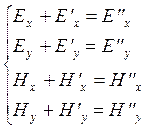(1)

Полагая, что в роли 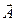был взят вектор 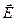, т.е. 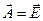, то 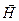можно взять из известного условия (3.14) перпендикулярност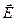и и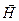

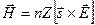, (9.4)

где 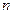- показатель преломления среды, 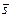- направляющий вектор луча, 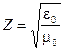(здесь учтено, что для оптических сред 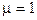и 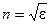). Если раскрыть векторное произведение (9.4) то получим, что 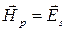и 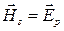. Подставляя значения векторов 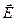и 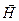выраженные через 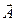в (9.3) и учитывая, что проекция отраженного луча на ось 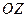движется в сторону, противоположную падающему и отраженному лучу (для этого меняем знак у 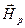, чтобы выполнялось правило буравчика), запишем

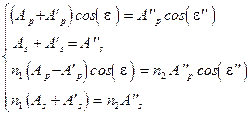(9.5)

Полученное выражение представляет собой систему четырех линейных уравнений с четырьмя неизвестными 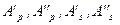, которыми являются компоненты преломленного и отраженного луча при заданных компонентах падающего луча, угле его падения и показателей преломления сред. Данная система распадается на две системы из двух уравнений с двумя неизвестными каждая, которые решаются без труда. В результате, после преобразований и с использованием закона преломления, получим

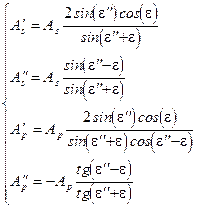(9.6а)     (9.6б)   (9.6в)     (9.6г)

Эти соотношения называются формулами Френеля. Из этих уравнений следует, что преобразования компонент у различных направлений колебаний векторов отличаются, т.е. состояние поляризации действительно меняется.

Отметим, что 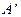и 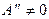ни при каких углах падения 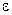(в случае 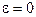неопределенность, этот случай будет рассмотрен позже). Это говорит о том, что преломленная и отраженная волны всегда присутствуют. Однако имеется одно исключение. Если выражение (9.6г) переписать, заменив тангенс отношением синуса к косинусу, то

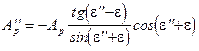. (10)

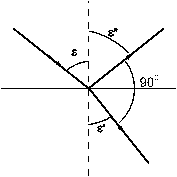Рис 9.4

При 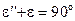амплитуда отраженной волны в плоскости падения 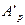равна нулю, т.е. в световой волне присутствует лишь одна компонента электромагнитного поля - в данном случае перпендикулярная плоскости падения. В этих случаях говорят, что волна плоско поляризована. Угол 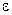, при котором этот эффект происходит, называется углом Брюстера и его величина может быть определена следующим образом. Из рис. 9.2 следует, что преломленный и отраженный луч взаимно перпендикулярны .

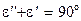Используя закон Снеллиуса 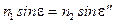и использовав условие 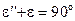, найдем, что 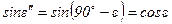. После подстановки в выражение для закона Снеллиуса получим

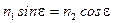, (11.а)

откуда

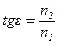. (11.б)

В частности для стекле в воздухе, когд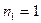а , а 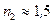- получим 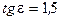, откуда .

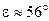Используя вектор Пойнтинга, можно получить энергетические характеристики отраженного и преломленного лучей - интенсивностей, т.к.

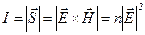, (12)

где 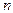- показатель преломления среды, а также коэффициенты отражения 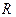и преломления 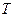, как отношения интенсивностей отраженной или преломленной волн к интенсивности падающей в соответствующих плоскостях 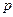и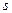

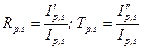. (13)

Используя (9), (12) и (13) запишем величины этих коэффициентов

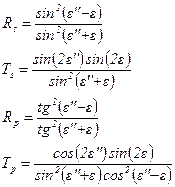(14)

Особый интерес представляет случай нормального падения, когда 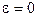. Непосредственная подстановка в уравнения (9) или (14) приведет к неопределенностям типа 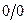. Однако, если их раскрыть, то выражения (14) существенно упростятся, при этом, как уже предполагалось, исчезнут различия в коэффициентах для разных плоскостей падения, при этом формулы (9) примут вид

,

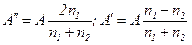(15)

а формулы (15) преобразуются в

.

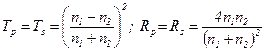(16)

Анализ полученных выражений позволяет сделать следующие выводы:

1) Так как при нормальном падении среда по отношению к лучу изотропна, что подтверждается формулами (15) , т.е. имеют вид, одинаковый для всех ориентаций векторов 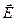или 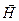, то состояние поляризации у отраженного и преломленного лучей такие же, как и падающего.

2) В случае 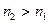знак у 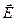или 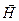меняется, что означает потерю половины волны при отражении от более плотной среды.

3) При любом прохождении границы часто энергии теряется на отражение, причем эти потери одинаковы при прямом и обратном направлении движения светового потока. Например, при прохождении границы воздух – стекло ( 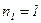, 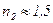); 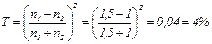. В сложных оптических системах, состоящих из большого числа поверхностей, разделенных воздухом, эти потери бывают весьма значительными. Например, у системы, состоящей из 5 линз, т.е. имеющей 10 поверхностей, эти потери составляют около 34%. Что бы их уменьшить, применяют специальные меры, например просветление.

4. Из (15) следует, что 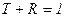. Это закон сохранения энергии.