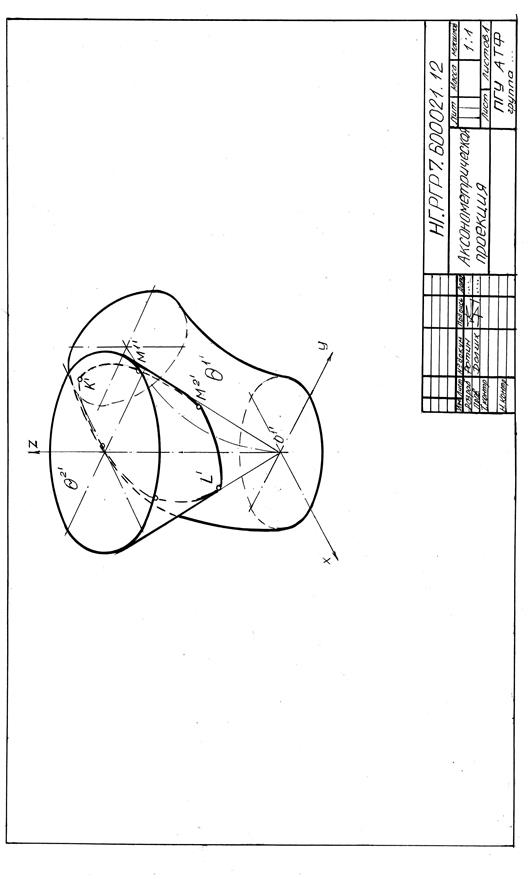
Принятые обозначения и терминология
Точки обозначаются прописными буквами латинского алфавита: А, В, С …
Вспомогательные точки обозначают арабскими цифрами: 1, 2, 3…
Линии (прямые и кривые) - строчные буквы латинского алфавита: a, b, c ...
Прямые, имеющие специальные обозначения: горизонталь - h, фронталь - f.
Углы в пространстве - строчные буквы греческого алфавита: α, β, γ…
Плоскости и поверхности в пространстве - прописные буквы греческого
алфавита: Δ, Σ, Ψ…
Плоскости проекций:- горизонтальная плоскость проекций - П1,
- фронтальная плоскость проекций - П2,
- профильная плоскость проекций - П3.
Дополнительные плоскости проекций: П4, П5, П6 …
Проекции точек, прямых и плоскостей: на П1 - А1,а1,Ψ1…, на П2 - А2, а2, Ψ2.
Следы прямой: горизонтальный след - h, фронтальный след -f
Способ задания геометрической фигуры:
m(АВ) - прямая m задана ее точками А и В,
Ω(c∩d) - плоскость Ω задана пересекающимися прямыми c и d ,
Σ(Σ1, Σ2) - плоскость Σ задана своими проекциями,
│ΑΒ│ - длина отрезка АВ.
Аксонометрическая плоскость проекций обозначается как П′ - буква П
греческого алфавита с добавлением значка «штрих».
Аксонометрические оси: х ′, y′, z′ .
Ортогональное (прямоугольное) проецирование – проецирование
параллельными лучами из бесконечности под прямым углом к плоскости проекций.
Ось проекций – линия пересечения плоскостей проекций. Ось х12 разделяет плоскости П1 и П2 , ось y13 разделяет плоскости П1 и П3 , ось z23 разделяет плоскости П2 и П3. Часто ось проекций на чертеже не проводится, но ее расположение всегда известно. Так, ось х12 всегда горизонтальна.
Линия проекционной связи (линия связи) – линия, перпендикулярная к оси проекций. На линии связи расположена пара проекций точки.
Геометрическая фигура – любое множество точек. К фигурам относится точка (множество, состоящее из одного элемента), прямая либо кривая линия, плоскость, поверхность, тело.
Конкурирующие точки – точки, проекционно совпадающие на одной из плоскостей проекций. Горизонтально конкурирующие точки имеют совпадающие проекции на горизонтальной плоскости проекций; фронтально конкурирующие точки имеют совпадающие проекции на фронтальной плоскости проекций.
Опорные точки – крайние точки (верхняя, нижняя, левая, правая, дальняя, ближняя) и точки перехода видимости.
Прямая общего положения – прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Прямая уровня – прямая, параллельная одной из плоскостей проекций.
Горизонталь (горизонтальная прямая уровня) параллельна плоскости П1.
Фронталь плоскости параллельна плоскости П2.
Профильная прямая – параллельна плоскости П3.
Проецирующая прямая – прямая, перпендикулярная одной из плоскостей проекций. Например, фронтально проецирующая прямая перпендикулярна фронтальной плоскости проекций. На эту плоскость прямая проецируется в виде точки.
Следы прямой – точки пересечения прямой с плоскостями проекций.
Плоскость общего положения – плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Проецирующая плоскость – плоскость, перпендикулярная одной из плоскостей проекций. На комплексном чертеже имеет вырожденную в прямую проекцию на той плоскости проекций, которой она перпендикулярна. Так, горизонтально проецирующая плоскость ┴П1 имеет проекцию на П1 в виде прямой.
Плоскость уровня – плоскость, параллельная одной из плоскостей проекций. Такие плоскости являются дважды проецирующими, так как на двух плоскостях проекций имеют вид прямой, расположенной под прямым углом к линиям связи.
Многогранник – замкнутая гранная поверхность, имеющая не менее четырех граней (пирамида, призма, тетраэдр и т. д.).
Поверхность вращения образуется вращением образующей l вокруг оси вращения i.
Поверхности 2–го порядка – поверхности, заданные алгебраическим уравнением 2–й степени (эллипсоиды, параболоиды, параболическая цилиндрическая поверхность и т. д.).
Очерк поверхности – проекция контура поверхности на плоскость проекций.
Аксонометрическая проекция – параллельная проекция предмета, дополненная изображением координатных осей с натуральными масштабными отрезками, отложенными на этих осях.
Приложение Е
(Рекомендуемое)
Образец выполнения РГР2
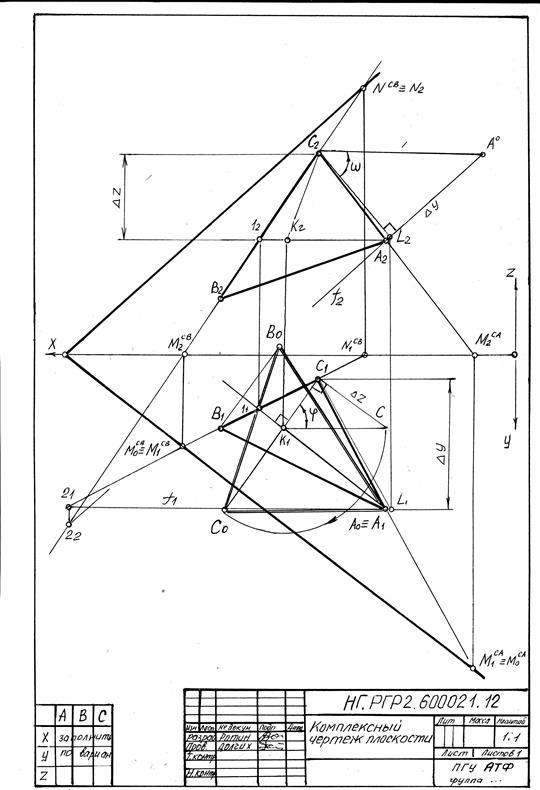
Приложение Ж
(Рекомендуемое)
Образец выполнения РГР3
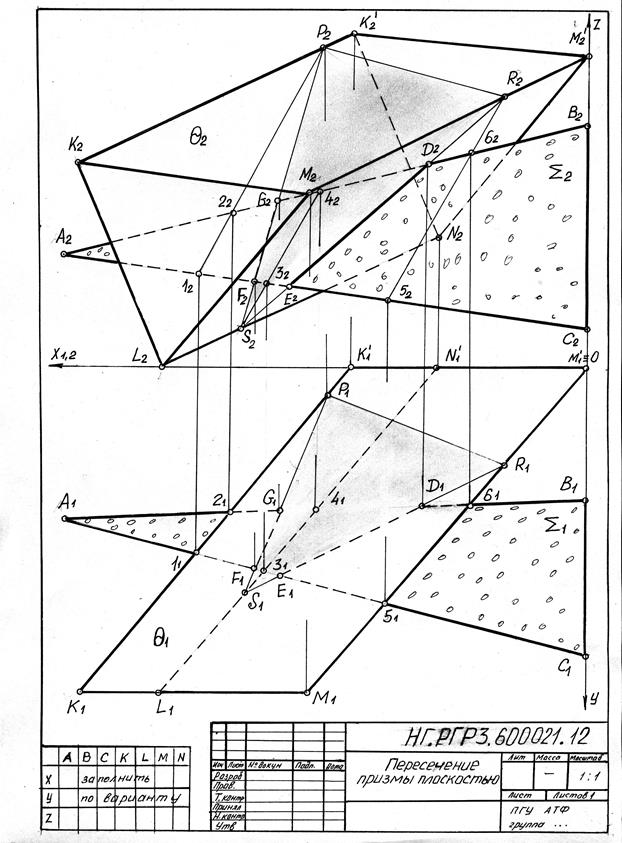
Приложение И
(Рекомендуемое)
Образец выполнения РГР4
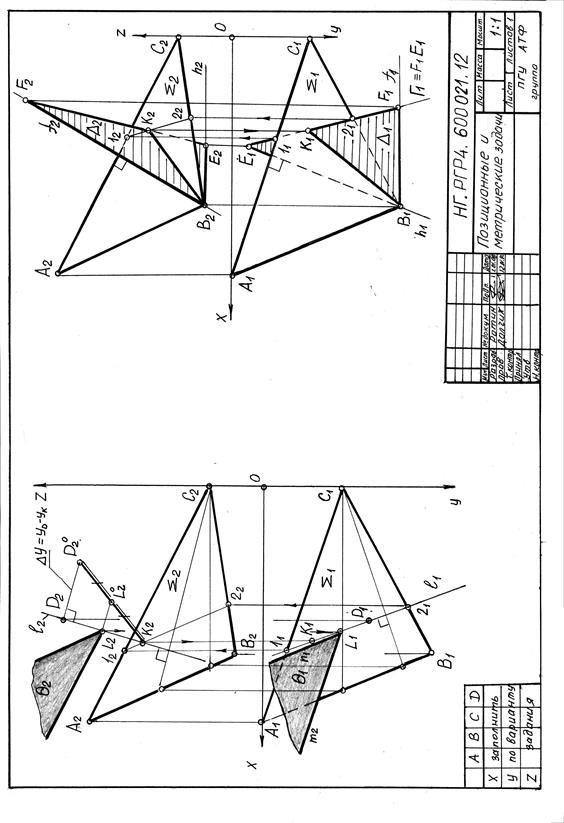
Приложение К
(Рекомендуемое)
Образец выполнения РГР5
 |
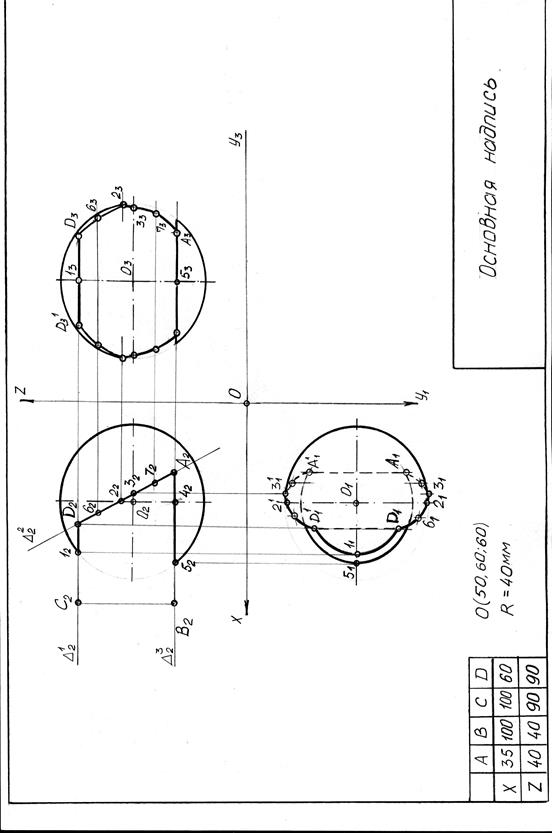
Приложение Л
(Рекомендуемое)
Образец выполнения РГР6
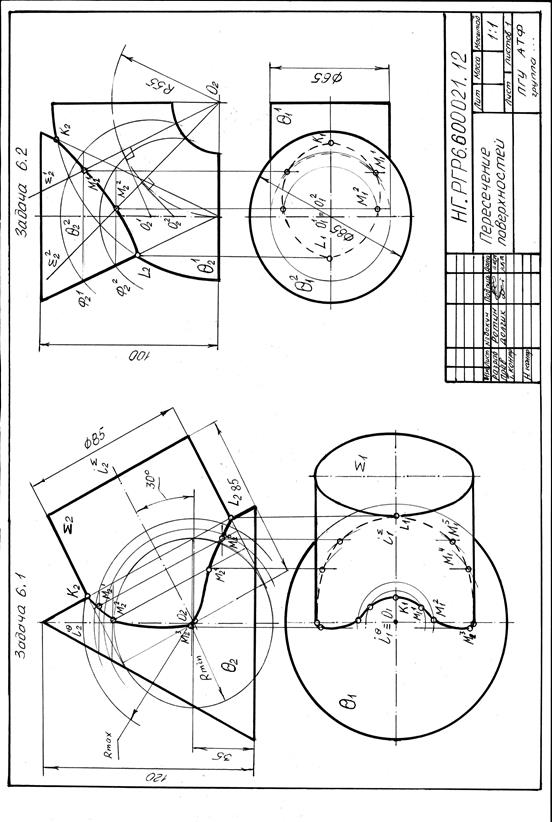
Приложение М
(Рекомендуемое)
Образец выполнения РГР7