Производная функции. Геометрический смысл производной

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

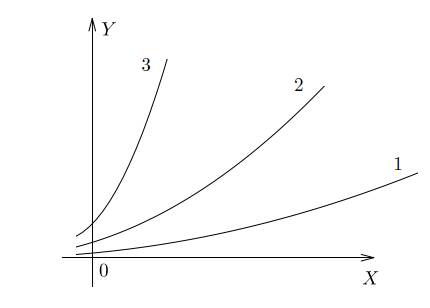
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

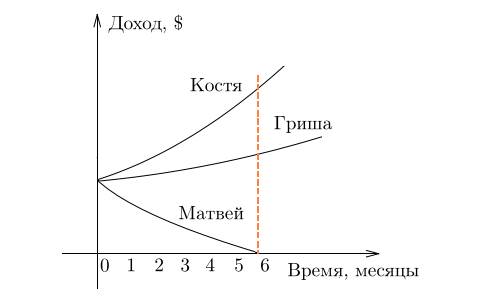
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .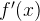

Покажем, как найти 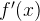с помощью графика.

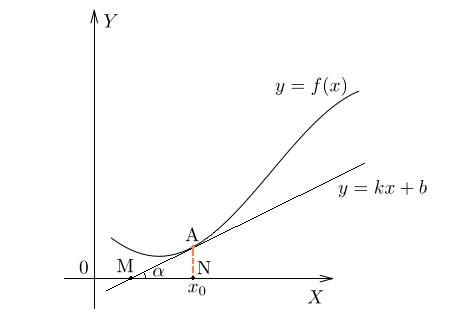
Нарисован график некоторой функции 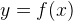. Возьмем на нем точку 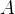с абсциссой 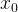. Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции 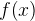в точке 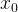равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

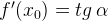
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .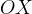

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком.

Найдем 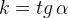. Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :

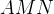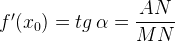
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .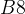

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

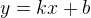Величина 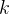в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

.

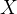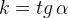Мы получаем, что

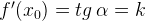
Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке 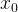равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции 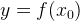. Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

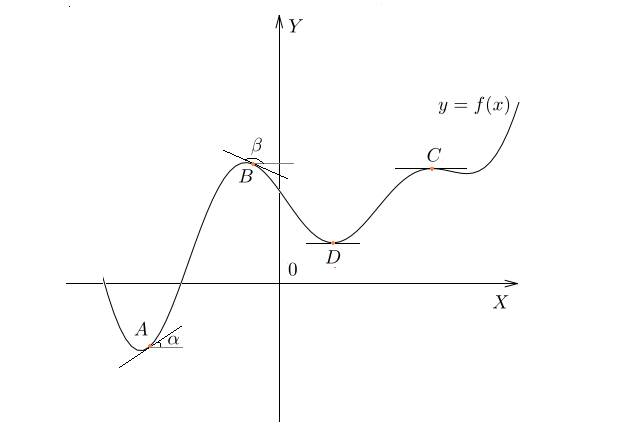
В точке 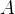функция 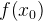возрастает. Касательная к графику, проведенная в точке 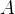, образует острый угол 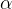; с положительным направлением оси 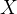. Значит, в точке 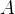производная положительна.

В точке 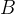наша функция убывает. Касательная в этой точке образует тупой угол 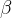; с положительным направлением оси 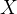. Поскольку тангенс тупого угла отрицателен, в точке 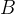производная отрицательна.

Вот что получается:

Если функция 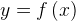возрастает, ее производная положительна.

Если 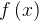убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках 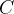(точка максимума) и 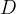(точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка 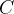— точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке 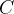с «плюса» на «минус».

В точке 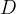— точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная 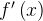положительна, то функция 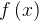возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

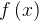	возрастает	точка максимума	убывает	точка максимума	возрастает

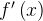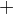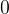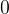Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи 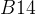. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

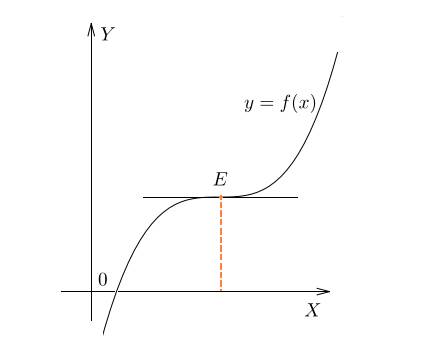
В точке 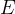касательная к графику горизонтальна, и производная равна нулю. Однако до точки 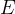функция возрастала — и после точки 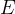продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

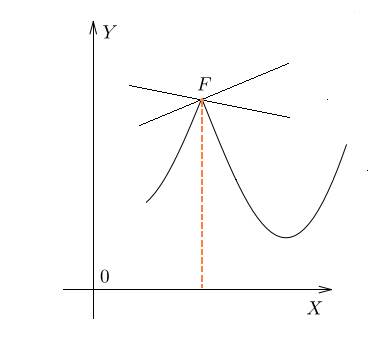
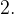Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных (см. выше).