Система макроскопических уравнений Максвелла. Векторы поляризации и намагниченности. Материальные уравнения и их простейшие примеры

Первое Максвелла уравнения имеет вид:
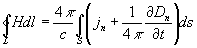, (1, a)
Второе Максвелла уравнения является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная) записывается в виде:

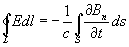, (1, б)
Третье Максвелла уравнения выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):

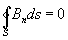, (1, в)
Четвёртое Максвелла уравнения (обычно называемое Гаусса теоремой) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:

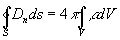, (1, г)
Если считать, что векторы электромагнитного поля (Е, В, D, Н) являются непрерывными функциями координат, то, рассматривая циркуляцию векторов Н и Е по бесконечно малым контурам и потоки векторов B и D через поверхности, ограничивающие бесконечно малые объёмы, можно от интегральных соотношений (1, а — г) перейти к системе дифференциальных уравнений, справедливых в каждой точке пространства, то есть получить дифференциальную форму Максвелла уравнения (обычно более удобную для решения различных задач):

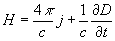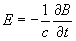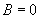rot , rot , div , div .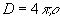

Здесь rot и div — дифференциальные операторы ротор (см. Вихрь) и дивергенция, действующие на векторы Н, Е, B и D. Физический смысл уравнений (2) тот же, что и уравнений (1).
Максвелла уравнения в форме (1) или (2) не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Необходимо их дополнить соотношениями, связывающими векторы Е, Н, D, В и j, которые не являются независимыми. Связь между этими векторами определяется свойствами среды и её состоянием, причём D и j выражаются через Е, а B — через Н:
D = D (E), B = B (Н), j = j (E). (3)
Эти три уравнения называются уравнениями состояния, или материальными уравнениями; они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определённую форму. В вакууме DºЕ и Bº Н. Совокупность уравнений поля (2) и уравнений состояния (3) образуют полную систему уравнений.
Макроскопические Максвелла уравнения описывают среду феноменологически, не рассматривая сложного механизма взаимодействия электромагнитного поля с заряженными частицами среды. Максвелла уравнения могут быть получены из Лоренца — Максвелла уравнений для микроскопических полей и определённых представлений о строении вещества путём усреднения микрополей по малым пространственно-временным интервалам. Таким способом получаются как основные уравнения поля (2), так и конкретная форма уравнений состояния (3), причём вид уравнений поля не зависит от свойств среды.