Степенные ряды. Область сходимости
В курсе математического анализа изучаются последовательности и ряды, членами которых являются не числа, а функции, определенные на некотором множестве. Такие функциональные последовательности и ряды широко применяются в различных приложениях для анализа и приближенных вычислений. Мы ограничимся рассмотрением степенных рядов.
Определение: Функциональный ряд вида
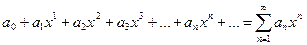 | (9.5.1) |
называется степенным рядом. Постоянные числа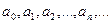 
называются коэффициентами степенного ряда (9.5.1).
При разных значениях переменной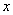 
мы получим разные числовые ряды, которые могут быть сходящимися или расходящимися. Особый интерес представляет множество значений x, при которых ряд (9.5.1) сходится, оно называется областью сходимости степенного ряда.
Очевидно, что частичная сумма степенного ряда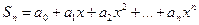 
представляет собой функцию переменной x. Стало быть, последовательность частичных сумм является функциональной последовательностью 
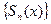и сумма ряда (9.5.1) является функцией переменной x: 
.
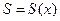Теорема: (Теорема Абеля). Если степенной ряд (9.5.1) сходится при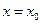 
и 
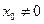, то он абсолютно сходится при всех x, таких, что 
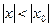. Если ряд (9.5.1) расходится при 
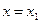, то он расходится и при всех x, удовлетворяющих неравенству 
.
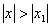Теорема Абеля примечательна утверждением, что если степенной ряд (9.5.1) сходится при 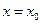, то он сходится абсолютно всюду на отрезке 
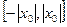. Если же 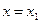– точка расходимости ряда, то он расходится везде вне интервала 
.
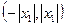Отсюда следует основополагающая в теории степенных рядов Теорема.
Теорема: Если степенной ряд (9.5.1) сходится не только при x=0, то существует такое положительное число R (возможно, и бесконечное), что ряд абсолютно сходится в интервале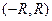 
и расходится везде вне этого интервала.
Число R и интервал 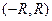называются соответственно радиусом сходимости и интервалом сходимости степенного ряда. Всякий степенной ряд имеет свой радиус сходимости 
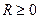. При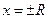 
вопрос о сходимости должен рассматриваться конкретно для каждого ряда.
Способ определения радиуса сходимости степенного ряда (9.5.1) указывает следующая Теорема.
Теорема
Если для степенного ряда (9.5.1) существует предел
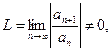 | (9.5.2) |
то радиус сходимости этого ряда определяется формулой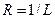 
.
Заметим, что если предел L (9.5.2) равен нулю, то степенной ряд сходится на всей числовой прямой, т.е.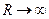 
.
Рассмотрим примеры на Определение радиуса сходимости степенного ряда.
Пример
Определить радиус сходимости ряда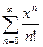 
.
Решение
Согласно Теореме 3, радиус сходимости этого ряда определяется по формуле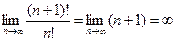 
, т.е. данный ряд абсолютно сходится на всей числовой оси.
Пример
Определить радиус сходимости ряда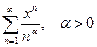 
.
Решение
Радиус сходимости находим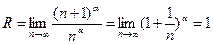 
. Радиус сходимости данного ряда 
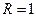. Выясним вопрос о сходимости ряда в точке 
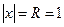. При подстановке в степенной ряд значения 
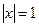, получим числовой ряд 
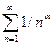, который имеет различный характер сходимости в зависимости от 
.
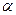а) при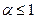 
ряд 
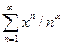сходится условно на отрезке 
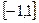как знакопеременный ряд, а на интервале 
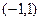он сходится абсолютно (т.к. 
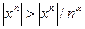и ряд 
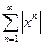сходится как сумма геометрической прогрессии со знаменателем 
).
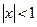б) При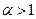 
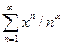ряд сходится абсолютно на отрезке .
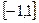Пример
Определить радиус сходимости ряда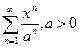 
.
Решение
Получаем: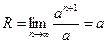 
. При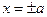 
получаем, что необходимое условие сходимости числового ряда не соблюдается. Следовательно, данный ряд сходится абсолютно на интервале 
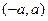как сумма геометрической прогрессии со знаменателем меньше единицы.
Пример
Определить радиус сходимости ряда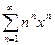 
.
Решение
Радиус сходимости ряда: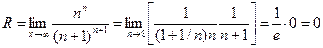 
Следовательно, данный ряд сходится лишь в точке x=0.
Свойства степенных рядов
Вообще говоря, сумма степенного ряда является функцией от переменной .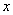
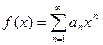 . | (9.5.3) |
Пусть интервал сходимости этого ряда (-R, R). Тогда говорят, что функция f(x) может быть разложена в степенной ряд на интервале (-R, R).
Степенные ряды обладают рядом свойств; два из них мы приведем без доказательства.
Степенной ряд можно дифференцировать почленно на промежутке его сходимости, так что
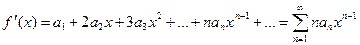 | (9.5.4) |
1. При этом интервал сходимости ряда (9.5.4) тот же, что и ряда (9.5.3). Таким же образом можно вычислить производные любого порядка.
2. Степенной ряд можно интегрировать почленно в интервале его сходимости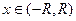 
, т.е. 
.
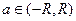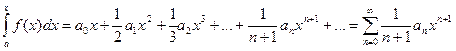
Замечание
Из свойства 1 следует, что сумма степенного ряда непрерывна на интервале его сходимости.
Ряд Маклорена
Теорема
Если функция f(x) может быть разложена на интервале (-R, R) в степенной ряд, то это разложение единственно.
Так как по условию теоремы ряд (9.5.3) сходится на интервале (-R, R) и f(x) – его сумма, то в силу свойства 1 этот степенной ряд можно дифференцировать почленно на указанном интервале сколько угодно раз. Тогда, дифференцируя n раз равенство (9.5.3), получаем
,
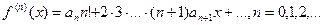откуда при x=0 находим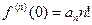 
, или
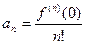 | (9.5.6) |
Таким образом, коэффициенты степенного ряда (9.5.3) однозначно определяются формулами (9.5.6).
Подстановка полученных коэффициентов в формулу (9.5.3) дает вид разложения функции f(x) в степенной ряд:
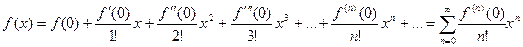 | (9.5.7) |
Ряд (9.5.7) называют рядом Маклорена для функции f(x).
Для любой бесконечно дифференцируемой функции можно составить ряд Маклорена.
Установим теперь связь между формулой Маклорена и рядом Маклорена.
Как известно, для любой (n+1) раз дифференцируемой функции справедлива формула Маклорена: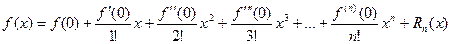 
,
,
где Rn(x) остаточный член в форме Лагранжа: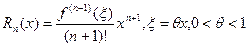 
.
Если Sn частичная сумма ряда Маклорена, то нетрудно видеть, что формула Маклорена может быть представлена в виде
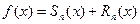 . | (9.5.8) |
Из представления (9.5.8) следует Теорема о сходимости ряда Маклорена.
Теорема
Для того, чтобы для бесконечно дифференцируемой функции f(x) имело место разложение (9.5.7) в ряд Маклорена на интервале (-R, R), необходимо и достаточно, чтобы остаточный член в формуле Маклорена для этой функции стремился к нулю на указанном интервале при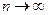 
:
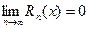 . | (9.5.9) |
Разложение элементарных функций в ряд Маклорена
Для того, чтобы разложить функцию в степенной ряд, необходимо найти коэффициенты ряда, определить радиус сходимости ряда и проверить выполнение условия (9.5.9) на интервале (-R, R).
1. 
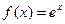. При x=0 получаем 
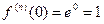, откуда по формулам (9.5.6) 
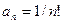. Далее определяем радиус сходимости степенного ряда с найденными коэффициентами.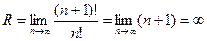 
, т.е. степенной ряд сходится на всей числовой прямой.
2. 
. 
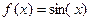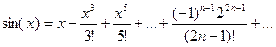Ряд сходится на всей числовой оси 
.
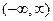3. 
. 
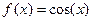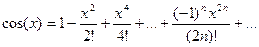Ряд сходится на всей числовой оси .
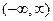4. 
. 
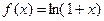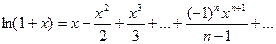
Понятие о функциональной последовательности, функциональный ряд
Определение
Функциональным рядом называется выражение
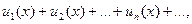 | (9.7.1) |
где u1(x), u2(x) (члены ряда) суть функции одного и того же аргумента x, определенные в некотором промежутке (a, b).
Определение
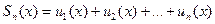 | (9.7.2) |
называется частичной суммой.
Определение
Совокупность значений x, при которых ряд сходится, называется областью сходимости функционального ряда.
Пример
Найти область сходимости и выражение суммы для ряда
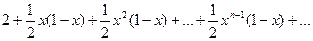 | (9.7.3) |
Решение
Запишем частичную сумму ряда (9.7.3) в виде
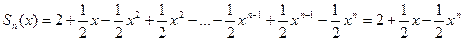 | (9.7.4) |
Если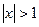 
, то 
при 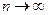не имеет конечного предела, т. е. ряд (9.7.3) расходится. При x=-1 ряд тоже расходится, так как 
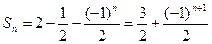попеременно принимает значения 2 и 1.
При остальных значениях x (т. е. при -1<x<1 )ряд (9.7.3) сходится.
Таким образом область сходимости ряда (9.7.3) есть промежуток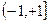 
. В этой области сумма S есть функция x, определяемая следующими равенствами:
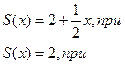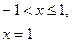  | (9.7.5) |
Определение
Если сумма S сходящегося в каждой точке промежутка (a, b) ряда (9.7.1) может быть вычислена с некоторой заданной точностью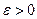 
для всех x сразу, начиная с некоторого номера n=N, то ряд (9.7.1) сходится на этом промежутке равномерно.
Если же ни один номер n не обеспечивает требуемой точности для всех x сразу, то ряд (9.7.1) сходится на промежутке (a, b) неравномерно.
Определение
Функциональный ряд
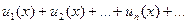 | (9.7.6) |
сходящийся в промежутке (a, b), называется равномерно сходящимся в этом промежутке, если остаток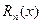 
, начиная с некоторого номера N, одного и того же для всех рассматриваемых значений x, остается по абсолютному значению меньшим любого заранее данного положительного числа e:
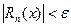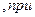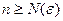    | (9.7.7) |
(номер N зависит только от e).
Если же для некоторого e условию (9.7.7) нельзя удовлетворить (для всех сразу) ни при каком значении N, то говорят, что ряд (9.7.6) в промежутке (a, b) сходится неравномерно.
Теорема (Признак равномерной сходимости)
Если каждый член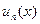 
функционального ряда (9.7.1) при любом x, взятом в промежутке (a, b), по абсолютному значению не превосходит положительного числа 
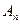и если числовой ряд
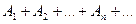 | (9.7.8) |
сходится, то функциональный ряд (9.7.1) в этом промежутке сходится равномерно.
Теорема (непрерывность суммы ряда)
Если все члены ряда
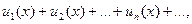| | (9.7.9) |
равномерно сходящегося в промежутке (a, b), являются непрерывными функциями, то и сумма ряда (9.7.9) есть непрерывная функция в промежутке (a, b).
Теорема (интегрирование рядов)
Если сходящийся ряд
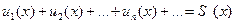 | (9.7.10) |
составленный из функций, непрерывных в промежутке (a, b), сходится в этом промежутке равномерно, то его можно интегрировать почленно. Ряд
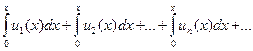 | (9.7.11) |
равномерно сходится в промежутке (a, b), и сумма его равна интегралу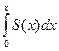 
от суммы ряда (9.7.10)
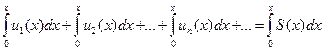 | (9.7.12) |
Теорема (дифференцирование рядов)
Если функциональный ряд
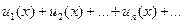 | (9.7.13) |
сходится в промежутке (a, b) и производные его членов непрерывны в этом промежутке, то ряд (9.7.13) можно почленно дифференцировать при условии, что полученный ряд
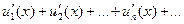 | (9.7.14) |
будет равномерно сходящимся в данном промежутке. Сумма ряда (9.7.14) будет производной от суммы ряда (9.7.13).
Тригонометрические ряды Фурье
Определение
Тригонометрическим рядом называется ряд вида
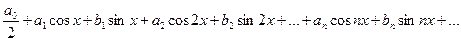 | (9.8.1) |
Здесь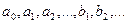 
– постоянные, называемые коэффициентами ряда.
Определение
Две функции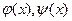 
называются ортогональными в промежутке (a, b), если интеграл произведения 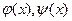, взятый в пределах от a до b, равен нулю.
Теорема
Любые две различные функции, взятые из системы функций
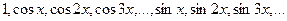 | (9.8.2) |
ортогональны в промежутке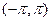 
.
Пусть дана функции f(x) с периодом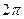 
. Требуется найти всюду сходящийся тригонометрический ряд
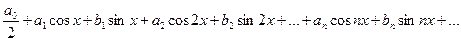| , | (9.8.3) |
имеющий сумму f(x).
Если эта задача имеет решение, то оно единственно, и коэффициенты искомого ряда (9.8.3) находятся по формулам Эйлера–Фурье:
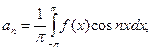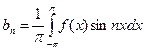  | (9.8.4) |
Полученный ряд называется рядом Фурье для функции f(x).
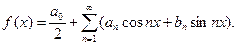 . | (9.8.5) |
Теорема
Если функция f(x). непрерывна на интервале [–l,l], то справедливо разложение
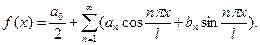 | (9.8.6) |
где
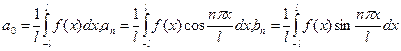 . | (9.8.7) |
Пример
Разложить в ряд Фурье функцию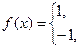 
Решение
Найдем коэффициенты разложения
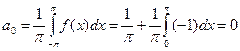
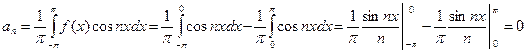
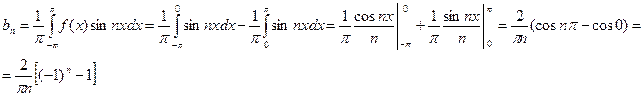
При четных n выражение в квадратной скобке равно нулю, а при нечетных n оно равно –2. Поэтому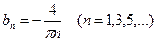 
. Таким образом 
.
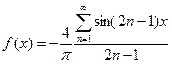Упражнения
Исследовать сходимость следующих рядов:
| 1. | 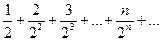 | 2. |  |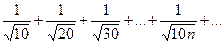
| 3. | 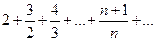 | 4. |  |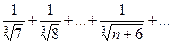
Исследовать сходимость рядов с заданными общими членами
| 5. | 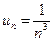 | 6. |  |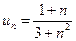
Выяснить, какие из нижеследующих рядов сходятся абсолютно:
| 7. |  |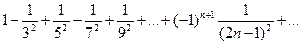
| 8. |  |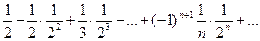
| 9. |  |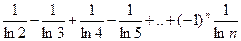
| 10. |  |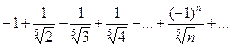
При каких значениях х сходятся ряды:
| 11. |  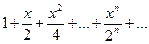| 12. |  |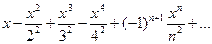
Литература
1. Бахвалов С.В., Бабушкин М.И., Иваницкая В.П.Аналитическая геометрия. – М.: Просвещение, 1970.
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984.
3. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1985.
4. Бугров Я.С., Никольский С.М.Дифференциальное и интегральное исчисление. – М.: Наука, 1988.
5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 1989.
6. Высшая математика для экономистов. Учебное пособие для вузов /Кремер Н.Ш. и др.: под редакцией проф. Кремера Н.Ш. – М.: Банки и биржи, ЮНИТИ, 1997.
7. Герасимчук В.С., Васильченко Г.С., Кравцов В.И.Курс классической математики в примерах и задачах: Учебное пособие. В двух частях. Ч.1. – Донецк, 2002. Ч.2 – Донецк, 2003.
8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2–х частях. – М.: Высшая школа, 1999.
9. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1977.
10. Ефимов Н.В.Краткий курс аналитической геометрии. – М.: Наука, 1975.
11. Ильин В.А., Позняк Э.Г. Основы математического анализа. – М.: Наука, 1982.
12. Ильин В.А., Поздняк Э.Г. Аналитическая геометрия. – М.:Физматгиз, 1968.
13. Клименко Е.П., Пахомова Н.Л., Самсонова Т.Н. Определенный интеграл: методические указания и контрольные задания – Владимир, 1996.- 40 с.
14. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 1986.
15. Мошнина Е.Н., Перельмутер Н.Л. Методические указания и типовой расчет по теме «Ряды» – Владимир, , 1997.- 44 с.
16. Мошнина Е.Н., Перельмутер Н.Л., Самсонова Т.Н. Методические указания и типовой расчет по теме «Дифференциальные уравнения» В 2-х ч. Ч.1 – Муром: ИПЦ МИ ВлГУ, 2000.- 38 с.
17. Мошнина Е.Н., Перельмутер Н.Л., Самсонова Т.Н. Методические указания и типовой расчет по теме «Дифференциальные уравнения» В 2-х ч. Ч.2 – Муром: ИПЦ МИ ВлГУ, 2000.- 42 с.
18. Плис А.И., Сливина Н.А. MathCad 2000. Математический практикум для экономистов и инженеров: Учеб.пособие. – М.: Финансы и статистика, 2000. – 656 с.
19. Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1985, тт. 1–2.
20. Привалов И.И. Аналитическая геометрия. – М.: Наука, 1964.
21. Сборник задач по математике для втузов: Линейная алгебра и основы математического анализа: В 2–х частях. Болгов В.А., Демидович Б.П., Ефименко В.А. и др. – М.: Наука, 1981.
22. Ушакова Л.В., Макаренко Л.Б. Методические указания и контрольные задания по теме «Введение в анализ» – Владимир, 1982.- 49 с.
23. Ушакова Л.В., Овчинников А.В., Мисеврина Н.А.Методические указания и контрольные задания по теме «Линейная алгебра и ее приложения» – Владимир, 1982.- 52 с.
24. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: В 3–х томах/ – М.: Наука, 1969.