Растяжение графика функции от оси ординат
Как построить график функции с помощью геометрических преобразований графиков.
Сжатие (растяжение) графика к (от) оси ординат.
Симметричное отображение графика относительно оси 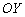
Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов:
Сжатие графика функции к оси ординат
Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.
Правило: чтобы построить график функции 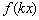 , где
, где  , нужно график функции
, нужно график функции 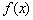 сжать к оси
сжать к оси 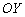 в
в 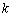 раз.
раз.
Пример 1
Построить график функции 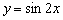 .
.
Сначала изобразим график синуса, его период равен 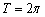 :
:

К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку  и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси 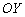 в 2 раза:
в 2 раза:

То есть, график функции 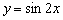 получается путём сжатия графика
получается путём сжатия графика 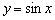 к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:
к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился: 
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
 Смотрим на чертёж, и видим, что это действительно так.
Смотрим на чертёж, и видим, что это действительно так.
Пример 2
Построить график функции 
«Чёрная гармошка» 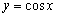 сжимается к оси
сжимается к оси 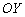 в 3 раза:
в 3 раза:

Итоговый график  проведён красным цветом.
проведён красным цветом.
Исходный период 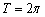 косинуса закономерно уменьшается в три раза:
косинуса закономерно уменьшается в три раза:  (отграничен жёлтыми точками).
(отграничен жёлтыми точками).
Растяжение графика функции от оси ординат
Это противоположное действие. Случай имеет место, когда АРГУМЕНТ функции умножается на число  .
.
Правило: чтобы построить график функции 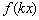 , где
, где  , нужно график функции
, нужно график функции 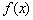 растянуть от оси
растянуть от оси 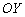 в
в  раз.
раз.
Продолжим мучить синус:
Пример 3
Построить график функции 
Берём в руки нашу «бесконечную гармошку»:

И растягиваем её от оси 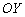 в 2 раза:
в 2 раза:

То есть, график функции  получается путём растяжения графика
получается путём растяжения графика 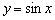 от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза:
от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза:  , он толком даже не вместился на данный чертёж.
, он толком даже не вместился на данный чертёж.
Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций:
Пример 4
Построить графики функций 
График функции  получается путём сжатия графика экспоненты
получается путём сжатия графика экспоненты 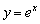 к оси
к оси 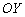 в два раза. А график
в два раза. А график  – путём растяжения графика экспоненты
– путём растяжения графика экспоненты 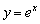 от оси
от оси 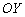 в два раза:
в два раза:

В качестве ассоциации можете опять поиграть на «баяне»  .
.
Продолжаем систематизировать умножение аргумента функции на число: 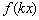
Мы рассмотрели два случая – сжатие (  ) и растяжение (
) и растяжение (  ).
).
Очевидно, что нет практического смысла рассматривать значения  . Есть более интересный вопрос: что происходит, когда аргумент умножается на отрицательное число? Ответ будет получен чуть позже, а пока рассмотрим распространённый частный случай, когда
. Есть более интересный вопрос: что происходит, когда аргумент умножается на отрицательное число? Ответ будет получен чуть позже, а пока рассмотрим распространённый частный случай, когда  :
:
