Численные методы решения систем нелинейных уравнений

Цель работы:сформировать у студентов представления о методах решения систем нелинейных уравнений, привить умения составлять и применять алгоритмы для решения таких систем уравнений, выработать навыки в использовании программных средств для решения систем уравнений.

Метод Ньютона

Пример 3.1.

Решить систему двух нелинейных уравнений

x+3lg(x) – y² = 0

2x² – xy – 5x + 1=0

методом Ньютона.

Решение.

1. Зададим координатную сетку и вычислим значения

координат х и у в узлах сетки (рис. 3.1).

2. Построим график функции и карты линий уровня (рис. 3.2)

(на которых наглядно видно, что данная система имеет

решение, и причем единственное) с использованием панели

Graph (рис. 3.3.).

n = 100

xmin = 1 xmax = 5 ymax = 5 ymin = 1

i = 0…n j = 0..n

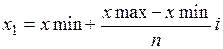
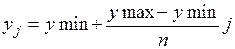
g(x,y) = 2x² – xy – 5x +1

M_i,j = g(x_i, y_j) N_i,j = q(x_i, y_j)

Рис. 3.1.Задание координатной сетки

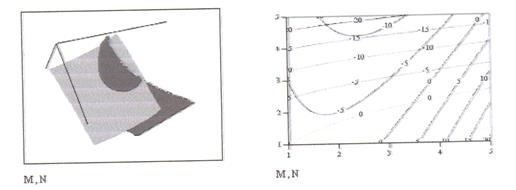
Рис. 3.2.График функции и карта линий уровня

Рис. 3.3.ПанельGraph

Точки пересечения линий одинакового уровня дают решение данной системы уравнений.

4. Зададим начальное приближение переменных:

х = 3.4 у = 2.2

5. Зададим функцию, содержащую решение системы уравнений

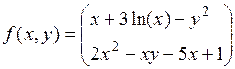
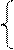x + 3lg(x) – y² = 0

2x² – xy – 5x + 1 = 0

Рис. 3.4.Вектор-функция, задающая систему уравнений

6. Зададим функцию (рис. 3.5.), реализующую метод Ньютона

(функция F возвращает таблицу, содержащую значения

координат х, у на каждом шаге итерации и соответствующие

значения координат вектор - функции).

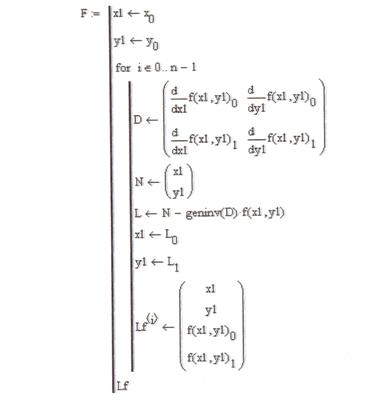
Рис. 3.5.Функция, возвращающая решение системы методом Ньютона

Запустив программу, получим итерационную последовательность (рис. 3.6), которая показывает, как находятся приближения. Здесь две первые строки – это значения х и у соответственно, а последние две строки – значения данных функций при найденных значениях х и у. В ноль функции обращаются на седьмом шаге. Значит, решением будет являться пара чисел х = 3,487 и

у = 2,262.

F =

	8,502	5,365	3,986	3,545	3,488	3,487	3,487	3,487
	5,573	3,475	2,578	2,298	2,262	2,262	2,262	2,262
	-19,771	-4,522	-0,857	-0,087	1,452·10-3	4,367· 10-7	997· 10-14
	55,679	13,1	2,568	0,265	4,435·10-3	1,333· 10-6	137· 10-13

Рис. 3.6.Итерационная последовательность, полученная для решения системы нелинейных уравнений по методу Ньютона

7. Визуализируем итерационный процесс (рис. 3.7), транспонируя для этого полученную матрицу F:

F1 = F^Т

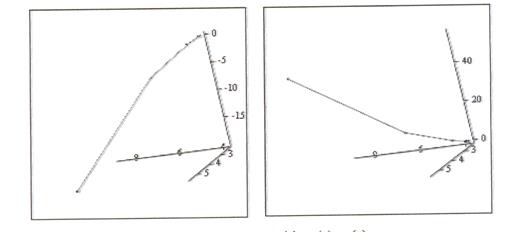
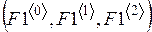
Рис. 3.7.Визуализация итерационного процесса

8. Проверяем решение системы нелинейных уравнений с помощью блока Given...Minerr (рис.3.8).

х = 3,4 у = 2,2 Given

х + 3log(x) – y² = 0

2x² – xy – 5x + 1 = 0

Z = Minerr (x, y

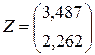
Рис.3.8.Проверка численного решения с помощью

встроенных функций пакета Mathcad

Вопросы по теме

Задание к лабораторной работе №3

Задание 3.1.

Решить систему двух нелинейных уравнений (табл. 3.1) методом Ньютона.

Таблица 3.1. Варианты заданий для самостоятельной работы

№	Задание	№	Задание
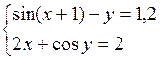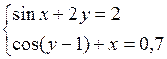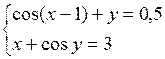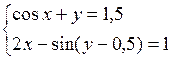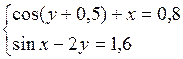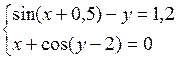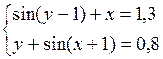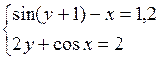5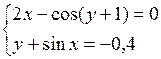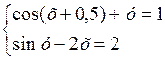

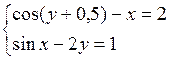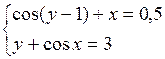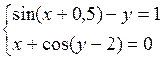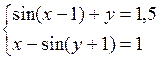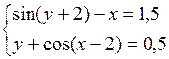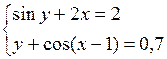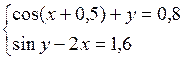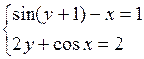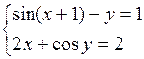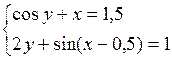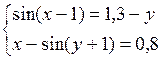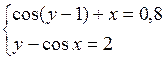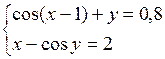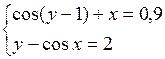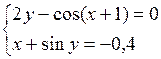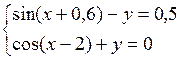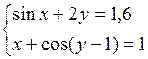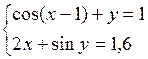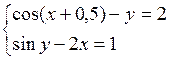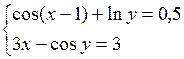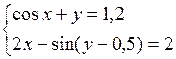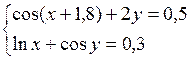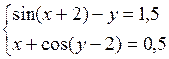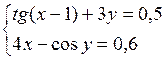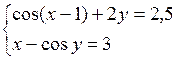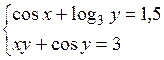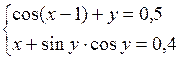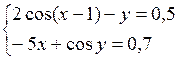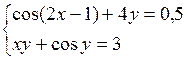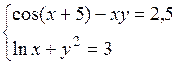Лабораторная работа№4

Численное интегрирование

Цель работы:ознакомиться с численными методами вычисления определенных интегралов, научиться решать задачи с использованием формулы Симпсона, трапеций, правых и левых прямоугольников, метода Монте-Карло и оценивать погрешность всех перечисленных формул.

Метод прямоугольников

Пример 4.1.

Вычислить приближенное значение интеграла 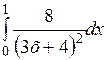, используя формулы левых и правых прямоугольников, при п = 1000.

Решение.

1. Задаем функцию f(x), отрезок [a, b] и функцию

нахождения дифференциалов п – го порядка.

2. Находим значение интеграла заданной функции для

использования его в дальнейшем решении для сравнения

(рис. 4.1).

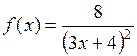
a = 0 b = 1 n = 10C

dif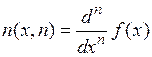

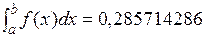
Рис. 4.1.Вычисление точного значения интеграла

Составим функцию, входными параметрами которой являются: а, b – левая и правая границы интервала; п – количество разбиений; char – если имеет значение “left”, то идет подсчет по формуле левых прямоугольников, любое другое – по формуле правых прямоугольников (рис. 4.2).

Погрешность показывает, что полученное значение интеграла верно до третьего знака после запятой.

Рис. 4.2.Функция, возвращающая значение интеграла,

найденного по формулам прямоугольников.

Результаты вычислений по формулам правых и левых прямоугольников:

Integr(a, b, n, “left”) = 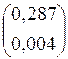Integr(a, b, n, “right) =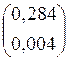

Метод Симпсона

Пример 4.2.

Вычислить приближенное значение интеграла ,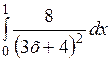

используя общую формулу Симпсона, при n = 1000.

Решение.

Составим функцию, входными параметрами которой являются: a, b – левая и правая границы интервала; n – количество разбиений. Индексы iEven и iUneven обозначают четность и нечетность соответственно (рис. 4.3.).

Simpson(a, b, n) =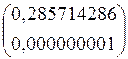

Рис 4.3.Функция, возвращающая значение интеграла

с помощью метода Симпсона

Следовательно, решением будет число, равное 0,285714286. Погрешность показывает, что полученное значение интеграла верно до девятого знака.

Метод трапеций

Пример 4.3.

Вычислить приближенное значение интеграла 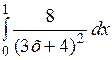, используя формулу трапеций (1.6.16), при п = 1000.

Решение.

Функция, реализующая вычисление интеграла методом трапеций, представлена на рис. 4.4.

Рис.4.4. Функция, возвращающая значение интеграла с

использованием формулы трапеций.

4.4. Метод Монте – Карло

Пример 3.4.

Вычислить приближенное значение интеграла 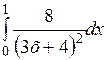, используя метод Монте – Карло, при п = 1000000.

Решение.

Реализация метода Монте – Карло для вычисления интеграла представлена на рис. 4.5.

Сравнивая точное и численное значение интегралов находим, что абсолютная погрешность равна 1,6·10^-4.

a = 0 b = 1 n = 1000000

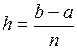
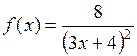
i = 0..n

x_i = a + (b – a) · md(1)

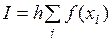
I = 0,285550681

Рис. 4.5.Ход решения задачи на нахождение значения

интеграла с помощью метода Монте – Карло

Вопросы по теме

1. В каком случае используется численное интегрирование?

2. Постановка задачи численного интегрирования.

3. Какие существуют методы интегрирования функции?

4. Графическая интерпретация метода трапеций.

5. Как оценить погрешность метода трапеций?

6. Графическая интерпретация метода Симпсона.

7. Как оценить погрешность метода Симпсона?

8. Графическая интерпретация метода прямоугольников.

9. Как оценить погрешность метода прямоугольников?

10. Чем отличаются формулы метода трапеций и метода

Симпсона?

11. Как влияет на точность численного интегрирования

величина шага h?

12. Чем отличается вычисление погрешности метода

трапеций и Симпсона?

13. Основная идея метода Монте – Карло.

14. Графическая интерпретация метода Монте – Карло.

Задание к лабораторной работе №4

Задание 4.1.

Найти приближенное значение интеграла заданной функции

f(x) на отрезке [a, b] по формулам трапеций, Симпсона,

прямоугольников, Монте – Карло при делении отрезка на

1000 равных частей, произвести оценку погрешности

методом интегрирования и сравнить точность полученных

результатов: составить функцию, возвращающую значение

интеграла на основе формулы метода Монте – Карло.

Сравнить результаты, полученные разными методами.

Таблица 4.1. Варианты заданий для выполнения самостоятельной

работы

№	F( x)	[a, b]
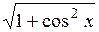		[0; 3]
	sin(2x2 + 1)	[0; 1]
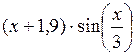		[1; 2]
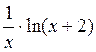		[2; 3]
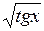		[0; 0,5]
	2,6 · x2 · ln x	[1,2; 2,2]
	(x2 + 1) · sin (x – 0,5)	[0,5; 1,5]
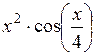		[2; 3]
	3x + ln x	[1; 2]
	3x2 + tg x	[-0,5; 0,5]
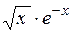		[0,1; 1,1]
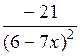		[-2; 0]
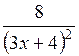		[0; 1]
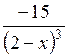		[3; 5]
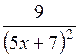		[2; 3]
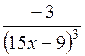		[-1; 0]
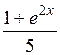		[0; 3]
	ex·sin(x2)	[0; 5]
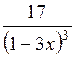		[-3; -1]
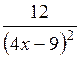		[0; 1]
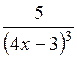		[4; 5]
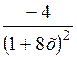		[0; 3]
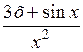		[0,1; 1,1]
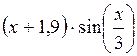		[1; 2]
		[1,5; 2,5]
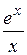		[1; 7]
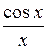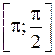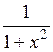		[0; 1]
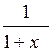		[0; 9]
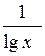		[4; 10]
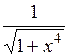		[0; 6]
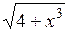		[0; 3]
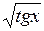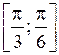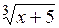		[0; 8]
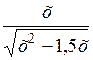		[2; 5]
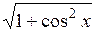		[0; π]
	(x – 5)2 (10 – x)	[0; 10]
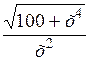		[2; 4]
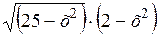		[0; 2]
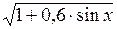		[0; π / 2]

Лабораторная работа №5