Численные методы решения систем линейных уравнений
Постановка задачи
Дана система n алгебраических уравнений с n неизвестными:
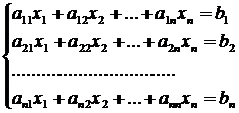 (1)
(1)
Эту систему можно записать в матричном виде: 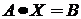 ,
,
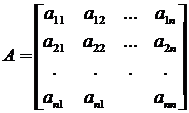 ;
; 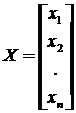 ;
; 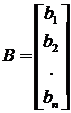 .
.
где A - квадратная матрица коэффициентов, X - вектор-столбец неизвестных, B - вектор-столбец свободных членов.
Численные методы решения систем линейных уравнений делятся на прямые и итерационные. Первые используют конечные соотношения для вычисления неизвестных. Пример - метод Гаусса. Вторые основаны на последовательных приближениях. Примеры - метод простой итерации и метод Зейделя.
Метод Гаусса
Метод основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается x1 из всех последующих уравнений. Затем с помощью второго уравнения исключается x2 из последующих и т.д. Этот процесс называется прямым ходом метода Гаусса и продолжается до тех пор, пока в левой части последнего n-го уравнения не останется лишь один член с неизвестным xn. В результате прямого хода система принимает вид:
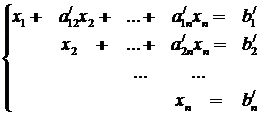 (2)
(2)
Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных, начиная с xn и кончая x1.
Метод простой итерации и метод Зейделя
Решение систем линейных уравнений с помощью итерационных методов сводится к следующему. Задается начальное приближение вектора неизвестных, в качестве которого обычно выбирается нулевой вектор:
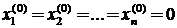 .
.
Затем организуется циклический вычислительный процесс каждый цикл которого представляет собой одну итерацию. В результате каждой итерации получается новое значение вектора неизвестных. Итерационный процесс заканчивается, если для каждой i-й компоненты вектора неизвестных будет выполнено условие
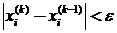 (3)
(3)
где k - номер итерации, e - заданная точность.
Недостатком итерационных методов является жесткое условие сходимости. Для сходимости метода необходимо и достаточно, чтобы в матрице A абсолютные значения всех диагональных элементов были больше суммы модулей всех остальных элементов в соответствующей строке:
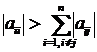 (4)
(4)
Если условие сходимости выполнено, то можно организовать итерационный процесс, записав систему (1) в приведенном виде. При этом слагаемые, стоящие на главной диагонали нормируются и остаются слева от знака равенства, а остальные переносятся в правую часть. Для метода простой итерации приведенная система уравнений имеет вид:
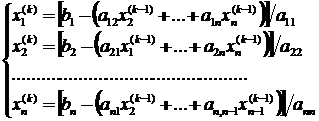 (5)
(5)
Отличие метода Зейделя от метода простой итерации заключается в том, что при вычислении очередного приближения вектора неизвестных используются уже уточненные значения на этом же шаге итерации. Это обеспечивает более быструю сходимость метода Зейделя. Приведенная система уравнений имеет вид:
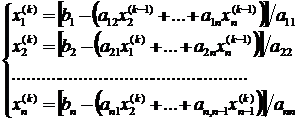 (6)
(6)
Реализация в пакете Excel
В качестве примера рассмотрим систему уравнений:
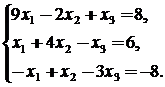
Данная система удовлетворяет условию сходимости и может быть решена как прямыми, так и итерационными методами. Последовательность действий (рис.7):
Оформить заголовок в строке 1 «Численные методы решения систем линейных уравнений».
В области D3:H6 ввести исходные данные, как показано на рисунке.
Ввести в ячейку F8 текст заголовка «Метод Гаусса» (выравнивание по центру).
Скопировать исходные данные E4:H6 в область B10:E12. Это - исходные данные для прямого хода метода Гаусса. Обозначим соответствующие строки A1,A2 и A3.
Подготовить место для первого прохода, обозначив в области G10:G12 названия строк B1,B2 и B3.
Ввести в ячейку H10 формулу «=B10/$B$10». Скопировать эту формулу на ячейки I10:K10. Это - нормировка на коэффициент a11.
Ввести в ячейку H11 формулу «=B11-H10*$B$11». Скопировать эту формулу на ячейки I11:K11.
Ввести в ячейку H12 формулу «=B12-H10*$B$12». Скопировать эту формулу на ячейки I12:K12.
Подготовить место для второго прохода, обозначив в области A14:A16 названия строк C1, C2 и C3.
Ввести в ячейку B14 формулу «=H10». Скопировать эту формулу на ячейки C14:E14.
Ввести в ячейку B15 формулу «=H11/$I$11». Скопировать эту формулу на ячейки C15:E15.
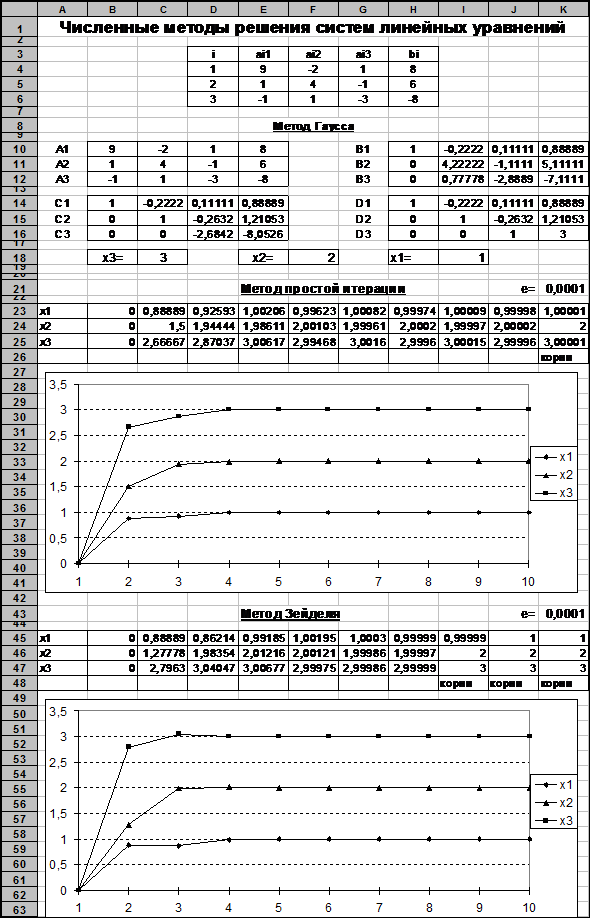
Рис. 7
12. Ввести в ячейку В16 формулу «=Н12-В15*$I$12». Скопировать эту формулу на ячейки С16:Е16.
13. Подготовить место для третьего прохода, обозначив в области G14:G16 названия строк D1, D2 и D3.
14. Ввести в ячейку H14 формулу «=В14». Скопировать эту формулу на ячейки I14:К14.
15. Ввести в ячейку H15 формулу «=В15». Скопировать эту формулу на ячейки I15:К15.
16. Ввести в ячейку Н16 формулу «=B16/$D$16». Скопировать эту формулу на ячейки I16:К16.
17. Подготовить место для обратного хода метода Гаусса, введя в ячейки В18, E18 и H18 соответствующие тексты «х3=», «х2=» и «х1=».
18. Ввести в ячейку С18 формулу «=К16». Получим значение переменной х3.
19. Ввести в ячейку F18 формулу «=К15-J15*К16». Получим значение переменной х2.
20.Ввести в ячейку I18 формулу «=K10-I10*F18-J10*C18». Получим значение переменной х1.
21. Ввести в ячейку F21 текст заголовка «Метод простой итерации» (выравнивание по центру).
22. Ввести в ячейку J21 текст «е=» (выравнивание по правому краю).
23. Ввести в ячейку К21 значение точности е (0,0001).
24. Обозначить в области А23:А25 названия переменных.
25. В области В23:В25 задать начальные значения переменных (нули).
26. Ввести в ячейку С23 формулу «=($H$4-$F$4*B24-$G$4*B25)/$E$4». Получим значение переменной х1 на первой итерации.
27. Ввести в ячейку С24 формулу «=($H$5-$E$5*B23-$G$5*B25)/$F$5». Получим значение переменной х2 на первой итерации.
28. Ввести в ячейку С25 формулу «=($H$6-$E$6*B23-$F$6*B24)/$G$6». Получим значение переменной х3 на первой итерации.
29. Ввести в ячейку С26 формулу «=ЕСЛИ(АВS(С23-В23)>$К$21;" "; ЕСЛИ(АВS(С24-В24)>$К$21;" ";ЕСЛИ(АВS(С25-В25)>$К$21;" "; '"корни")))». Это - проверка на достижение заданной точности (при этом печатается сообщение «корни»).
30. Выделить диапазон С23:С26 и скопировать его до столбца К, используя прием протаскивания. При появлении в строке 26 сообщения «корни» соответствующий столбец будет содержать приближенные значения переменных х1, x2, x3, которые являются решением системы уравнений с заданной точностью.
31. В области А27:К42 построить диаграмму, показывающую процесс приближения значений переменных х1, х2, x3 к решению системы. Диаграмма строится в режиме «График», где по оси абсцисс откладывается номер итерации.
32. Ввести в ячейку F43 текст заголовка «Метод Зейделя» (выравнивание по центру).
33. Ввести в ячейку J43 текст «е=» (выравнивание по правому краю).
34. Ввести в ячейку К43 значение точности е(0,0001).
35. Обозначить в области А45:А47 названия переменных.
36. В области В45:В47 задать начальные значения переменных (нули).
37.Ввести в ячейку С45 формулу «=($H$4-$F$4*B46-$G$4*B47)/$E$4». Получим значение переменной х1 на первой итерации.
38.Ввести в ячейку С46 формулу «=($H$5-$E$5*C45-$G$5*B47)/$F$5». Получим значение переменной х2 на первой итерации.
39. Ввести в ячейку С47 формулу «=($H$6-$E$6*C45-$F$6*C46)/$G$6». Получим значение переменной x3 ,на первой итерации.
40. Ввести в ячейку С48 формулу «=ЕСЛИ(АВ5(С45-В45)>$К$43;" "; ЕСЛИ(АВS(С46-В46)>$К$43;" ";ЕСЛИ{АВS(С47-В47)>$К$43;" ";"корни")))».
41. Выделить диапазон С45:С48 и скопировать его до столбца К, используя прием протаскивания. При появлении в строке 26 сообщения «корни» соответствующий столбец будет содержать приближенные значения переменных х1, х2, x3, которые являются решением системы уравнений с заданной точностью. Видно, что метод Зейделя сходится быстрее, чем метод простой итерации, то есть заданная точность здесь достигается за меньшее число итераций.
42. В области А49:К62 построить диаграмму, показывающую процесс приближения значений переменных х1, х2, x3 к решению системы. Диаграмма строится в режиме «График», где по оси абсцисс откладывается номер итерации.
3.5. Решение задачи межотраслевого баланса (модель Леонтьева)
Основой многих линейных моделей производства является схема межотраслевого баланса. Идея метода впервые в явном виде была сформулирована в работах советских экономистов в 20-х годах и получила затем развитие в трудах В.В Леонтьева по изучению структуры американской экономики. Предположим, что производственный сектор народного хозяйства разбит на п отраслей. Причем каждая отрасль выпускает продукт только одного типа, а разные отрасли выпускают разные продукты. Кроме того, в процессе производства своего вида продукта каждая отрасль нуждается в продукции других отраслей. В качестве примера рассмотрим упрощенную модель межотраслевого баланса, предполагая, что экономика страны состоит из 3-х отраслей (промышленности, сельского хозяйства и транспорта).
Введем следующие обозначения уi - конечный спрос на продукцию i-й отрасли, хi - выпуск продукции i-й отрасли. cij - доля продукции отрасли i, потребленной в процессе производства продукции отрасли j. В этом случае в соответствии с моделью Леонтьева имеем следующую систему линейных уравнений:
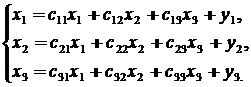
Задача состоит в нахождении неизвестных x1, x2, x3. Остальные величины считаются заданными. Заметим, что все коэффициенты cijизменяются в пределах от 0 до 0,3. Это обеспечивает сходимость при использовании итерационных методов.
Последовательность действий при реализации модели в пакете Excel с использованием метода простой итерации (рис. 8).
1. Ввести в ячейку H1 текст заголовка «Модель Леонтьева» (выравнивание по центру).
2. Ввести в ячейку H2 текст «Данные» (выравнивание по центру).
3. В области F4:J7 ввести исходные данные как показано на рисунке.
4. Обозначить в области А9:А12 номер итерации k и названия переменных х1, х2, x3.
5. В области В9:В12 задать начальные значения переменных (нули).
6. В ячейку С9 ввести 1, выделить ячейки В9 и С9 и, используя прием протаскивания, заполнить ряд до столбца О.
7. Ввести в ячейку С10 формулу «=($J$5+$H$5*B11+$I$5*B12)/(1-$G$5)». Получим значение переменной х1 на первой итерации.
8. Ввести в ячейку С11 формулу «=($J$6+$G$6*B10+$I$6*B12)/(1-$H$6)». Получим значение переменной х2 на первой итерации.
9. Ввести в ячейку С12 формулу «=($J$7+$G$7*B10+$H$7*B11)/(1-$I$7)». Получим значение переменной х3 на первой итерации.
10. Выделить диапазон С10:С12 и скопировать его до столбца О, используя прием протаскивания
11. В области A14:O33 построить диаграмму, показывающую процесс приближения значений переменных х1, х2, х3 к решению системы. Диаграмма строится в режиме «Точечная», где по оси абсцисс откладывается номер итерации.
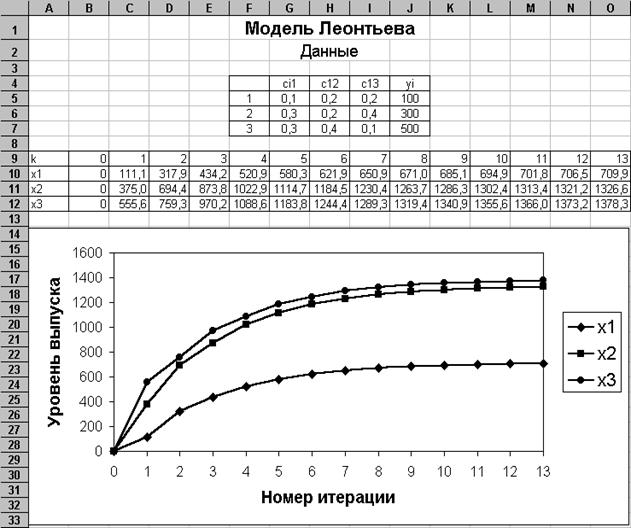 |
Рис. 8
