D-бөлшектеу тәсілімен орнықтылық аймақтарын көрсету

Сипаттамалық теңдеу берілсін

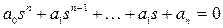. (5.47)

Мұнда екеуінен басқа (мысалы, а₀ және a_n) барлық коэффициенттер анықталған.

Ұйғарайық, а₀ және a_n белгіленген кейбір мәндерінде берілген теңдеу (5.47) түбірлер кеңістігінде k түбірі жорамал оське қарағанда сол жағында, ал n – k түбірі жорамал осьтің оң жағында орналассын деп. Белгілі бір шекте коэффициенттер а₀ және a_n мәнін өзгерту сипаттамалық теңдеу (5.47) жорамал осьтің оң жағында және сол жағында орналасқан түбірлер санын өзгертпейді делік. Сондықтан а₀, a_n жазықтығында мұндай аймақтарды бөліп көрсетуге болады, оның әр нүктесі көпмүше (5.47) анықтайды, сонымен қатар k түбірді жорамал осьтің сол жағында және n – k түбірді жорамал осьтің оң жағында орналасқанын анықтайды.

Жоғарыда мысал ретінде (5.47) теңдеуі қарастырылды. Онда бірінші және соңғы коэффициенттен басқаларының мәні берілген. Осыған ұқсас, егер басқа коэффиценттері берілген сандар болса, онда (5.47) теңдеуін D(k) аймақтарына бөлшектеуді кез келген екі коэффициенттер кеңістігінде жүргізуге болады. k саны кез келген бүтін мән қабылдауы мүмкін, осылай k-ның әртүрлі мәніне а₀, a_n жазықтығында аймақтарды көрсетуге болады. Коэффициенттер көп болған жағдайда, көп өлшемді коэффициенттер кеңістігін қарастыру керек және D(k) аймағы гипербеттермен бөлінеді. Осылай, коэффициенттер кеңістігін бөлшектеу D-бөлшектеу деп аталады.

Егер а коэффициентінің мәнін баяулатып үздіксіз өзгертетін болсақ, түбірлер біртіндеп оң жазықтыққа өтуі мүмкін. Бұл өту тек жорамал ось арқылы немесе шексіздік арқылы орындалуы мүмкін. Түбір шексіздікке тең болуы мүмкін, егер параметрлердің мәні а₀ коэффициентін нольге айналдырса.

Түбірлер жазықтығында түбірдің жорамал ось арқылы өтуі коэффициенттер кеңістігінде түбірдің D-бөлшектеу шекарасы арқылы өтуіне сәйкес келеді. Осыдан, D-бөлшектеуінің шекарасын анықтау тәсілі белгіленеді: ол, зерттелетін полиномда s айнымалысын jω (мұндағы ω – айнымалы шама, ал 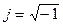) параметрлік алмастыру арқылы анықталады. Бұл мағынада D-бөлшектеуінің шекарасы түбірлер жазықтығындағы жорамал осьті сипаттамалық теңдеулер коэффициенттері кеңістігіне бейнелеу болып табылады. Сондай-ақ, D-бөлшектеуді кез келген параметрлер кеңістігінде жүргізуге болады, одан сипаттамалық теңдеудің коэффициенттері тәуелді болса болғаны. Түбінде тек D(k) орнықтылық аймағын бөліп көрсетсе болғаны.

Сонымен, D-бөлшектеу тәсілі бойынша жүйенің орнықтылық шекарасын анықтау үшін оның сипаттамалық теңдеу (5.47) таза жорамал мән s = jω қойылады, сонымен қатар ω айнымалысы -∞-тен +∞-ке дейін өзгертіледі. Осылай, жиілік ω шектелген мәндерінде тербелмелі орнықтылық шекарасы анықталады, ал жиіліктің ω = 0 және ω = ±∞ жеке мәндерінде (a_n = 0 және a₀ = 0 мәндеріне сәйкес келетін) қалған шекаралары анықталады.

Бірақ, s = jω болғанда жүйе тек қана орнықтылық шекарасында ғана болмауы мүмкін. Орнықтылық шекарасын алу үшін бұл теңдеудің оң нақты бөлікті түбірлерінің жоқ болу шартын қамтамасыз ету қажет (басқаша жүйе шекарада болмайды, яғни орнықсыз болады).

D-бөлшектеу тәсілін алдымен орнықтылық шекарасын бір параметр бойынша анықтауға, одан кейін екі параметр бойынша анықтауға пайдалануды қарастырайық.

Ұйғараық, орнықтылыққа әсерін анықтауға қажет белгілі бір параметр k сипаттамалық теңдеуге төмендегідей жолмен кіретін болсын деп

.

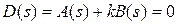Онда s = jω алмастырудан кейін аламыз

.

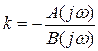Бұл теңдіктің оң жағының нақты мәні орнықтылық шекарасы болады. Оны табу үшін комплексті жазықтықта (k, Y) мысалы, сурет 5.15 көрсетілгендей ω жиілігінің -∞ < ω ≤ 0 және одан кейін 0 ≤ ω < ∞ өзгерген кездегі 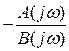функциясының годографын саламыз.

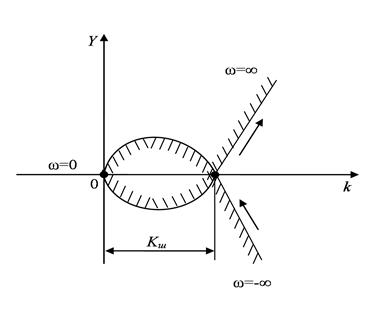
Сурет 5.15

Қисық сызықты штрихтау жиіліктің өсу бағыты бойынша жүрген кезде сол жақтан жүргізіледі. Годорафтың k нақты осімен қиылысқан нүктелері орнықтылық шекараларын анықтайды және теңсіздік 0 ≤ k ≤ K_ш болады.

Сурет 5.15 бойынша жүйенің сипаттамалық теңдеуі D(s) = 0 қанша (m) түбірі түбірлер жазықтығындағы жорамал осьтың оң жағында жатқанын анықтауға болады. Егер шекара екі қисық сызықтың қиылысуынан алынса (мысалы K_ш нүктесі), онда m = 2 болады, яғни шекарадан өткен кезде қос комплексті түбір оң нақты бөлікті K_ш < k болады.

Егер де шекарада k осі бір қисықпен қиылысса (мысалы k = 0 нүктесіндегідей), онда одан кейін (k < 0) m = 1 шекараның сыртындабір оң нақты түбір болады.

Осыған сәйкес k = K_ш орнықтылық шекарасы тербелгіш, ал k = 0 шекараcы апериодикалық болады.

Мысал. Сипаттамалық теңдеу берілсін

.

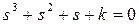Oны k параметріне байланысты шеше отырып 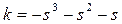аламыз және s = jω алмастыруын жүргізіп табамыз

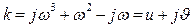
мұндағы .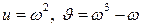

D-бөлшектеу шекарасын u, 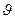жазықтығында жүргіземіз, ескере отырып k = 0 болғанда аламыз: u = 0, 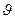= 0; k = 1 болғанда u = 1 және 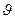= 0 болады; k → ∞ аламыз u → ∞, → ∞.

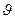Қисық сызық бойымен ω = -∞-тен ω =∞ бағытында жүріп сол жақты штрихтаймыз. Айқын, жорамал осьтің сол жағында ең саны көп түбірлері бар көпмүшелікке сәйкес (полиномға сәйкес келетін аймақ) штрихталған аймақ болады (сурет 5.16).

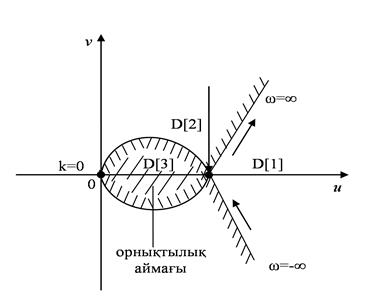
Сурет 5.16. Мысал үшін орнықтылық аймағын құрастыру

Бұл аймақ орнықтылық аймағы болатынына көз жеткізу үшін k = 0 шекаралық нүктені алып қарастырамыз. k = 0 болғанда қарастырылатын теңдеу мына теңдеуге келтіріледі

.

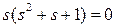Оның түбірлері

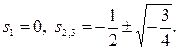
Яғни, бір түбірі – нольдік, ал екеуі жорамал осьтің сол жағында жатады. Қарастырылатын жорамал осьтің сол жағында орналасқан аймақтың ішінде түбірлер саны бірге артық болуы керек. Шындығында да, бұл жағдайда D-бөлшектеу шекарасынан штрихталған аймаққа қарай кіреміз. Сонымен, бұл аймақта барлық үш түбір де жорамал осьтің сол жағында жататын полиномдарға сәйкес келеді.

Маңыздысы, орнықтылық аймағына жататын k-ның тек нақты мәндері. Олар бірден u осінің D[3] аймағында жатқан кесіндісімен анықталады. Сонымен, орнықтылық шартын қарастырылған жүйенің 0 < k < 1 мәндері қанағаттандырады.

Екі параметр жазықтығында орнықтылық аймағын қарастыру. Кез келген екі параметр k, T бойынша орнықтылық аймағын жазықтықта құрастыру үшін сипаттамалық теңдеуге s = jω қойғаннан кейін аламыз

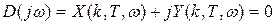
немесе

.

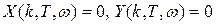Осыдан 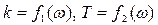болады. Алынған өрнекке ω-ның әртүрлі мәнін қоя отырып, (k, T) жазықтығындаалдымен -∞ < ω ≤ 0, одан кейін 0 ≤ ω < ∞ нүктелер бойынша қисық сызықты саламыз. Әр қисық сызықты штрихтау ω жиілігінің ұлғаю бағытында қисықтың бойымен жүрген кезде сол жақтан жасалады, егер де якобиан, яғни төменде көрсетілген анықтауыш оң болғанда

.

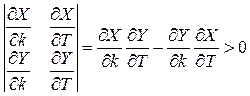Керісінше болған жағдайда қисықты штрихтау оң жақтан жүргізіледі.

Егер жиілік -∞ < ω < ∞ аралығында өзгергенде қисық сызық екі рет жүгіріліп өтілсе, онда оған штрихтау да екі рет жасалынады (сурет 5.17 қисық сызықтардың біреуін қараңыз).

Мұндай қисық сызықтар тербелмелі орнықтылық шекарасына сәйкес келеді, онда қос комплексті түбірлер нақты бөліктерінің таңбасын минустан плюске өзгертеді. Ерекше қисық сызықтар (көп жағдайда түзу сызықтар) ω = 0 және ω = ±∞ мәндеріне сәйкес келеді. Оның бойында ω (0 немесе ∞) тұрақты мәнін сақтайды. Оны штрихтау (бір-ақ рет) жасалынады, сурет 5.17 көрсетілгендей және жоғарыдағы айтылғандармен үйлеседі. Бір рет штрих-

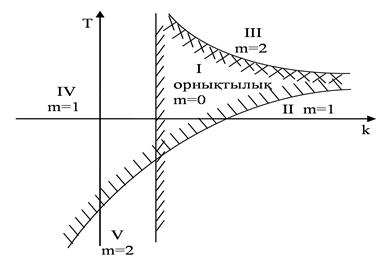
Сурет 5.17

талған қисық сызықтар нақты түбірдің теріс мәннен оң мәнге ноль немесе шексіздік арқылы өтуіне сәйкес келеді. Штрихтау бағытталған аймақта, нақты бөлігі оң түбірлер ең азы болады. Сондықтан, орнықтылық аймағын табу үшін D-бөлшектеу қисық сызықтары арасынан сондайын іздеу керек, қайсысына штрихтардың барлығы ұмтылғанын. Сурет 5.17 І-ші аймақ осындай аймақ болып табылады. Осыған түбегейлі көз жеткізу үшін бұл аймақтың кез келген бір нүктесі үшін (яғни k және T белгілі бір қос мәні үшін) орнықтылық критерийлерінің (Михайлов немесе Гурвиц бойынша) орындалуын тексеру керек. Онда І аймақта оң нақты бөлікті түбірлер саны m = 0 болады. Аймақ ІІ алсақ – m = 1, аймақ ІІІ – m = 2, аймақ IV – m = 1, ал аймақ V – m = 2 болады.

Жоғарыда қарастырылған мысалда жүйенің сипаттамалық теңдеуі мына түрде берілсін

.

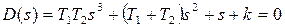Бұл теңдеуге s = jω қойып, нақты және жорамал бөлігін бөліп аламыз

.

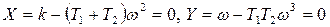Орнықтылық аймағын (k, T₁) параметрлер жазықтығында іздейтін боламыз. Жазылған теңдеулерден табамыз (егер ω ≠ 0)

.

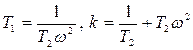Жиілік -∞ < ω < 0 өзгергенде гипербола бойымен жүреміз (сурет 5.18), сондай-ақ 0 < ω < ∞ өзгергенде тағы да ол бойынша өтеміз.

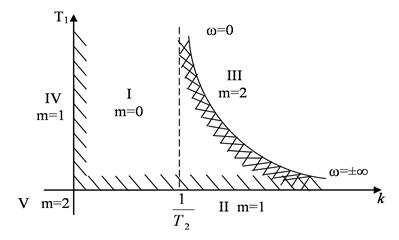
Сурет 5.18

Штрихтау бағытын анықтау үшін якобианды жазамыз

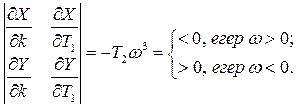
Бірінші жағдайда штрихтау оң жақтан, екінші жағдайда сол жақтан. Штрихтау бірінің үстіне бірі түседі (сурет 5.18).

Бұл гиперболадан басқа ерекше екі түзу аламыз: T₁ = 0, егер ω = ±∞ және k = 0 (жоғарыда жазылған соңғы Х = 0 теңдеуінен тікелей шығады).

Орнықтылық аймағы – аймақ І. Аймақ ІІ – m = 1, аймақ ІІІ – m = 2, аймақ IV – m = 1, аймақ V – m = 2 болады.