Задачи для самостоятельного решения
Задача 1. Пусть A и B – произвольные события. Упростить выражения: a) 
, b) 
, c) 
.
Ответ: a) 
; b) 
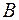; c)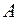 
.
 |
Задача 2. Электрическая цепь изображена на схеме 8.1. События
, 
, – контакт замкнут. Записать событие 
{лампочка зажглась}. Схема 8.1
Ответ: 
Задача 3.
 |
Электрическая цепь, состоящая из шести ламп
, 
, 
, 
, 
, 
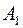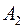имеет видПусть события 
заключаются в перегорании ламп 
. Будет ли цепь замкнута, если выполняются следующие события:
1) 
;
2) 
;
3) 
;
4) 
?
Ответ: 1) нет, 2)да, 3) нет, 4)нет.
Задача 4. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; b) сумма выпавших очков равна восьми, а разность – четырём; c) сумма выпавших очков равна пяти, а произведение – четырём.
Ответ: a) 
; b) 
, c) .
Задача 5. Найти вероятность того, что при бросании трёх игральных костей шестёрка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).
Ответ: 
.
Задача 6. В ящике 10 одинаковых деталей, помеченных номерами 1,2,…,10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлечённых деталей окажутся: а) деталь № 7; б) детали № 1 и № 2.
Ответ: а) 
б)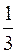 
.
Задача 7. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
Ответ: 
.
Задача 8. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
Ответ: .
Задача 9. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.
Ответ: 
.
Задача 10. Брошены три монеты. Найти вероятность того, что выпадут два “герба”.
Ответ: 
.
Задача 11.Орнитологи поймали в заповеднике 100 птиц, окольцевали их и выпустили. На следующий день они поймали 130 птиц, 10 из которых оказались окольцованы. Найти а) вероятность того, что пойманная птица окажется окольцованной; b) количество птиц в заповеднике.
Ответ: а) 
; b) 
.
Задача 12. На паркет, составленный из правильных треугольников со стороной а, случайно брошена монета радиуса r. Найдите вероятность того, что монета не заденет границы ни одного из треугольников.
Ответ: 
.
Задача 13.Точка (c, q) наудачу выбирается из квадрата с вершинами (-1,-1),(1,-1), (1,1), (-1,1). Найдите вероятность того, что корни уравнения 
действительные.
Ответ: 
.
Задача 14. По радиоканалу в течение промежутка времени 
передаются два сигнала длительностью 
, причем каждый из них начинается в любой момент интервала 
. Если сигналы перекроют друг друга хотя бы частично, оба они искажаются. Найти вероятность того, что сигналы будут приняты без искажений
Ответ: 
.
Задача 15. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
Ответ: 
.
Задача 16. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов равновозможно в течение данных суток. Найдите вероятность того, что одному из пароходов придется ждать освобождения причала, если время стоянки первого парохода 1 ч, а второго – 2 ч.
Ответ: 
.
Задача 17. Доказать, что если A и B – независимые события с положительными вероятностями, то они совместны.
Задача 18.В группе 25 студентов. Занятие проводятся, если хотя бы один студент явился на него. Пусть – { 
-й студент пришел на занятие}. Выписать следующие события:
a) 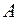= {занятие состоится};
b)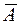 
= {занятие не состоится};
c) 
= {на занятие придет хотя бы один студент};
d) 
= {на занятие придут менее двух студентов}.
Ответ: а) 
; b) 
; c) 
; d) 
.
Задача 19.Известно, что курс евро к рублю может возрасти с вероятностью 0,55, а курс доллара к рублю – с вероятностью 0,35. Вероятность того, что возрастут оба курса, составляет 0,3. Найти вероятность того, что курс евро или доллара к рублю не возрастет.
Ответ: 
Задача 20.Событие 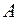состоит в том, что потенциальный покупатель увидел рекламу по телевизору, событие 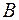– увидел рекламу в сети Internet. Известно, что 
, 
. Проверить справедливость следующих утверждений:
a) События 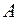и 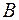несовместны;
b) События 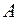и 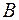противоположны;
c) 
.
Ответ: а) неверно ; b) неверно; c) верно;
Библиографический список
1. Вентцель, Е. С., Задачи и упражнения по теории вероятностей: Учеб. пособие для студ. втузов. / Е.С. Вентцель, Л.А. Овчаров; –М: Издательский центр «Академия», 2003– 448 с.
2. Вентцель, Е. С., Прикладные задачи теории вероятностей / Е.С. Вентцель, Л.А. Овчаров; –М: «Радио и связь», 1983– 416 с.
3. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман;– М.: Высш. Школа, 1997 – 400 с.
4. Гутер, Р.С. Основы теории вероятностей / Р.С. Гутер, Б.В. Овчинский; Из-во «Просвещение»: М, 1967. – 160 с.
5. Кузнецов, В.А. Математика – 8 для студентов. Теория вероятностей Учеб. Пособ./ В.А.Кузнецов, Ю.П. Самарин; Самар. гос. техн. ун-т. Самара, 2001– 131 с.
6. Симушкин, С.В./ Задачи по теории вероятностей: учеб. пособие / С.В. Симушкин, Л.Н. Пушкин. – Казань: Казан.ун-т, 2011 – 223 с.
7. Стрелкова, Н.Н. Основные понятия теории вероятностей: метод.указ./ Н.Н. Стрелкова; под. ред. М.А. Евдокимова; Самар. гос. техн. ун-т.– Самара, 2010. – 16 с.
8. Стрелкова, Н.Н. Непосредственное вычисление вероятности: метод.указ./ Н.Н. Стрелкова; под. ред. М.А. Евдокимова; Самар. гос. техн. ун-т.– Самара, 2010. – 18 с.
9. Чернова, Н.И. Теория вероятностей: Учебное пособие / Н.И. Чернова; Новосибирский гос. ун.-т: Новосибирск, 2007. – 160 с.
Оглавление
1. ОСНОВНЫЕ ПОНЯТИЯ.. 3
2. ВЕРОЯТНОСТЬ НА ДИСКРЕТНОМ ПРОСТРАНСТВЕ ЭЛЕМЕНТАРНЫХ СОБЫТИЙ.. 8
3. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 10
4. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 13
5. ГЕОМЕТРИЧЕСКИЕ ВЕРОЯТНОСТИ.. 16
6. АКСИОМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 19
7. РЕШЕНИЕ ЗАДАЧ.. 28
8. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.. 62
Библиографический список. 67
Понятие «Вероятность»
Составители Евдокимов Михаил Александрович
Бейлина Наталья Викторовна
Технический редактор
Компьютерная верстка
Подп. в печать Формат 60×84 1/16
Бум. офсетная. Печать офсетная. Усл. п. л.
Усл. кр.-отт. Уч.-изд. л. Тираж экз.
_________________________________________________________________
Государственное образовательное учреждение
высшего профессионального образования
«Самарский государственный технический университет»
443100 г. Самара, Молодогвардейская, 244. Главный корпус
Отпечатано в типографии Самарского
государственного технического университета
443100 г. Самара, ул. Молодогвардейская, 244. Корпус №8