Методы решения уравнений с частными производными.
Дифференциальные уравнения с частными производными
Классификация дифференциальных уравнений с частными производными
Определение. Дифференциальные уравнения с частными производными – это уравнения, содержащие неизвестную функцию нескольких переменных и ее частные производные.
Уравнения с частными производными можно классифицировать по многим признакам. Классификация уравнений важна потому, что для каждого класса существует своя общая теория и методы решения уравнений.
Рассмотрим несколько основных методов классификации таких уравнений.
1. Порядок уравнения. Порядком уравнения называется наивысший порядок частных производных, входящих в уравнение.
Например
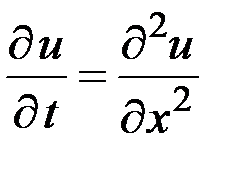 – уравнение второго порядка;
– уравнение второго порядка;
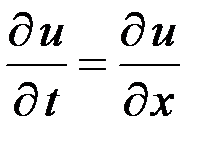 – уравнение первого порядка;
– уравнение первого порядка;
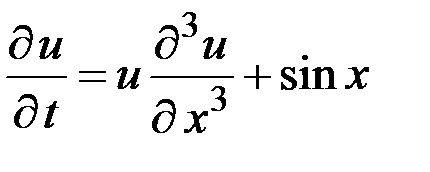 – уравнение третьего порядка.
– уравнение третьего порядка.
2. Число переменных. Числом переменных называется число независимых переменных.
Например
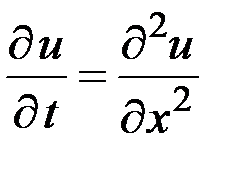 (уравнение с двумя переменными x и t);
(уравнение с двумя переменными x и t);
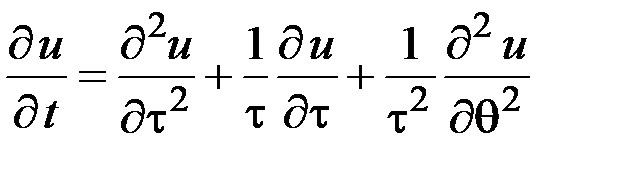 (уравнение с тремя переменными τ, θ t).
(уравнение с тремя переменными τ, θ t).
3. Линейность. Уравнения с частными производными бывают линейными и нелинейными.
В линейные уравнения зависимая переменная и все ее частные производные входят линейным образом, в частности они не умножаются друг на друга, не возводятся в квадрат и т.д.
Например
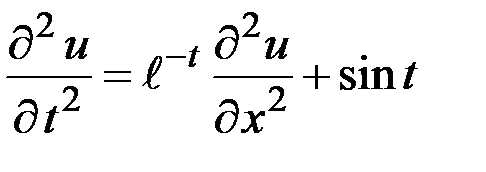 – линейное уравнение;
– линейное уравнение;
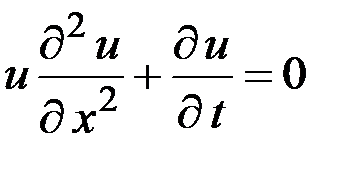 – нелинейное уравнение;
– нелинейное уравнение;
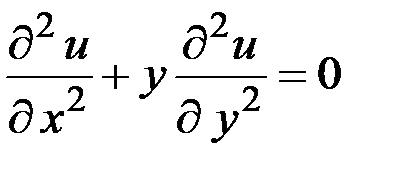 – линейное уравнение;
– линейное уравнение;
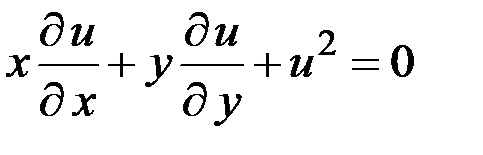 – нелинейное уравнение.
– нелинейное уравнение.
Линейным уравнением второго порядка с двумя независимыми переменными называется уравнение
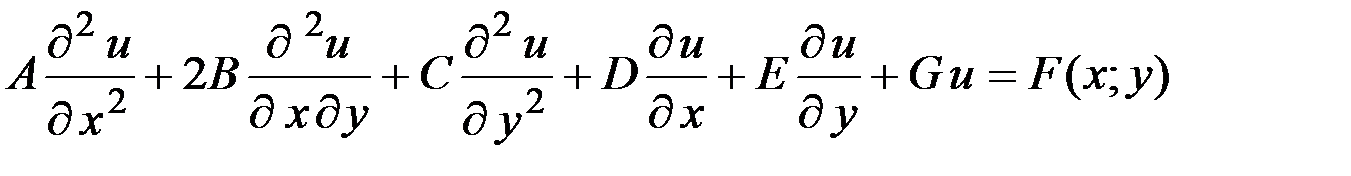 , (18.1)
, (18.1)
где A, B, C, D, E, G, F – константы или заданные функции независимых переменных x и y:
4. Однородность. Уравнение (18.1) называется однородным, если правая часть 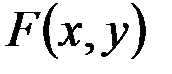 тождественно равна нулю для всех x и y.
тождественно равна нулю для всех x и y.
Если 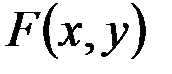 не равна тождественно нулю, то уравнение называется неоднородным.
не равна тождественно нулю, то уравнение называется неоднородным.
5. Виды коэффициентов. Если коэффициенты A, B, C, D, E, G уравнения (18.1) постоянны, то уравнение называется уравнением с постоянными коэффициентами (в противном случае уравнением с переменными коэффициентами).
Методы решения уравнений с частными производными.
Перечислим основные:
1. Метод разделения переменных. Он сводится к тому, что уравнение с частными производными с n независимыми переменными приводится к n обыкновенным дифференциальным уравнениям.
Это в случае полного разделения переменных. При частичном разделении переменных одно уравнение с частными производными сводится к нескольким уравнениям с частными производными с меньшим числом независимых переменных.
2. Метод преобразования координат. Исходное уравнение с частными производными сводится к обыкновенному дифференциальному уравнению или к другому, более простому уравнению с частными производными с помощью соответствующего преобразования координат (например, поворота координатных осей и т.п.).
3. Метод интегральных преобразований. Уравнение с частными производными с n независимыми переменными сводится к уравнению с частными производными с 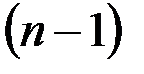 независимыми переменными; следовательно, уравнение с частными производными с двумя независимыми переменными можно свести к обыкновенному дифференциальному уравнению.
независимыми переменными; следовательно, уравнение с частными производными с двумя независимыми переменными можно свести к обыкновенному дифференциальному уравнению.
Это в случае одномерного интегрального преобразования. В случае 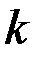 - мерного интегрального преобразования уравнение с частными производными с n независимыми переменными сводится к уравнению с частными производными с
- мерного интегрального преобразования уравнение с частными производными с n независимыми переменными сводится к уравнению с частными производными с 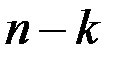 независимыми переменными.
независимыми переменными.
4. Преобразование зависимой переменной. Исходное уравнение с частными производными преобразуется к такому уравнению с частными производными для другой неизвестной функции, которое решается легче, чем исходное.
5. Численные методы. Исходное уравнение с частными производными сводится к системе разностных уравнений, которая решается методом итераций на ЭВМ.
Во многих случаях – это единственный способ решить уравнение с частными производными.
Кроме разностных методов решения уравнений с частными производными существуют и другие численные методы, в том числе и основанные на аппроксимации решения полиномиальными поверхностями (аппроксимация сплайнами).
6. Метод теории возмущений. Исходная нелинейная задача сводится к последовательности линейных задач, аппроксимирующих нелинейную задачу.
Точнее это метод линеаризации нелинейных задач. Общая теория возмущений содержит линейную и нелинейную теорию возмущений, каждая из которых в свою очередь бывает регулярной и сингулярной.
7. Вариационные методы. Вместо уравнения с частными производными решается некоторая задача минимизации. Оказывается, что функция, доставляющая минимум некоторому выражению (типа полной энергии системы) является в то же время решением исходного уравнения с частными производными.
Эти методы применимы к специальным задачам, что обусловлено существованием соответствующих выражений – функционалов для этих задач.
8. Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника.
Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.
9. Метод разложения по собственным функциям. Решение уравнения с частными производными ищется в виде ряда по собственным функциям.
Эти собственные функции находятся как решения так называемой задачи на собственные значения, соответствующей исходной задаче для уравнения с частными производными.
10. Метод интегральных уравнений. Уравнение с частными производными сводится к интегральному уравнению (уравнению, в котором неизвестная функция стоит под знаком интеграла). Существует много различных методов решения интегральных уравнений.
