Матричним способом
Обмежимось розглядом системи 3-х лінійних рівнянь
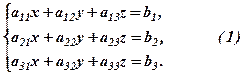
Запишемо такі матриці:
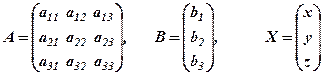 ,
,
де 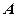 складена з коефіцієнтів при невідомих — матриця системи,
складена з коефіцієнтів при невідомих — матриця системи, 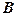 – матриця вільних членів,
– матриця вільних членів, 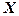 – матриця невідомих. Знайдемо добуток
– матриця невідомих. Знайдемо добуток
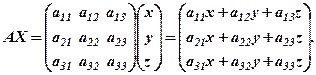
Користуючись означенням рівності матриць, ми бачимо, що система ЛР (1) є не що інше, як рівність відповідних елементів матриць – стовпців 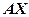 і
і 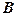 . Тому початкова система (1) набуває форму матричного рівняння
. Тому початкова система (1) набуває форму матричного рівняння

Для розв’язання останнього домножимо зліва рівняння (2) на обернену матрицю 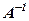 , вважаючи, що
, вважаючи, що 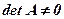 , отримаємо
, отримаємо
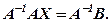
Але 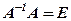 , а
, а 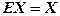 , тоді розв’язок матричного рівняння (2) запишеться
, тоді розв’язок матричного рівняння (2) запишеться
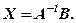 (3)
(3)
Покажемо, що з формули (3) можна отримати формули Крамера. Дійсно, підставляючи в (3) вирази для 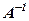 і
і 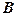 , маємо
, маємо
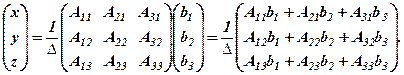
За теоремою про заміщення кожний елемент останньої матриці дорівнює значенням допоміжних визначників 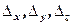 , які були введені при розв’язуванні систем за формулами Крамера. Тому далі маємо
, які були введені при розв’язуванні систем за формулами Крамера. Тому далі маємо
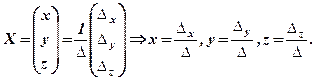
Звернемо увагу на те, що в формулі (3) співмножник 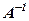 , залежить тільки від коефіцієнтів при невідомих, а
, залежить тільки від коефіцієнтів при невідомих, а 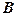 тільки від вільних членів. Тому, коли приходиться розв’язувати системи вигляду (1) з однаковими лівими частинами і різними вільними членами, то в таких випадках матричний розв’язок (3) стає зручнішим: обернену матрицю
тільки від вільних членів. Тому, коли приходиться розв’язувати системи вигляду (1) з однаковими лівими частинами і різними вільними членами, то в таких випадках матричний розв’язок (3) стає зручнішим: обернену матрицю 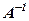 знаходимо тільки один раз і перемножуємо на нову матрицю
знаходимо тільки один раз і перемножуємо на нову матрицю 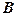 . В той же час, за формулами Крамера прийшлося б заново обчислювати допоміжні визначники
. В той же час, за формулами Крамера прийшлося б заново обчислювати допоміжні визначники 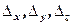 відповідно для кожного нового набору вільних членів.
відповідно для кожного нового набору вільних членів.
Приклад 1.Розв’язати систему рівнянь матричним способом
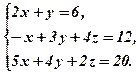
Складемо матрицю системи
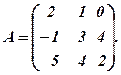
Для цієї матриці в 1.12. ми вже знайшли 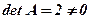 і обернену матрицю
і обернену матрицю
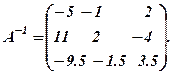
Тому згідно (3) маємо
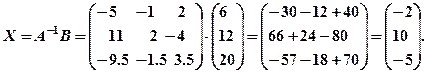
Отже, 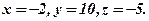
Пропонуємо перевірити відповідь.
