Розв’язання. 1) Канонічне рівняння параболи має вигляд

1) Канонічне рівняння параболи має вигляд .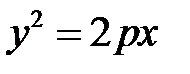

Підставимо у це рівняння координати точки А. Маємо 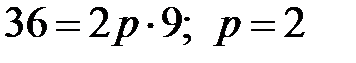. Отже відповідь: .

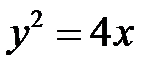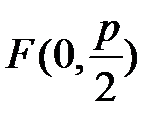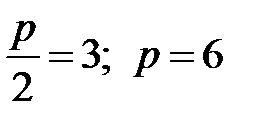2) Оскільки координати фокуса задаються формулою , то . Отже відповідь: .

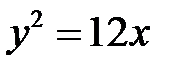Задача 43.4.Записати рівняння еліпса, фокуси якого розташовані на осі 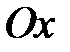симетрично відносно початку координат, точка 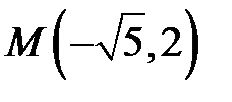належить еліпсу, а відстань між директрисами дорівнює 10.

Розв’язання.

Оскільки точка 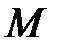належить еліпсу, то її координати здовольняють рівняння :

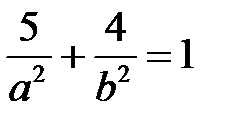, або .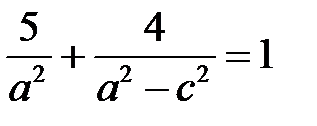

Відстань між директрисами дорівнює

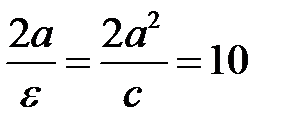, звідки .

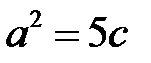Отримали систему рівнянь

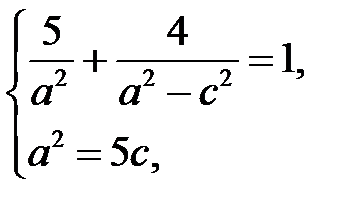
розв’язки якої

.

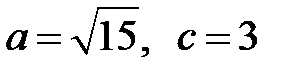Отже,

,

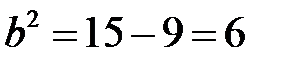і шукане рівняння еліпса набуває вигляду:

.

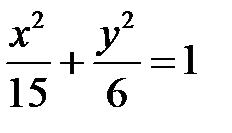Задача 43.5.На правій гілці гіперболи 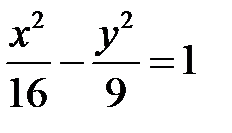знайти точку, відстань від якої до правого фокуса в два рази менша від відстані до лівого фокуса.