Метод областей 3 страница
Имеем
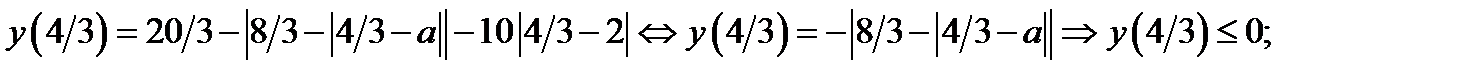
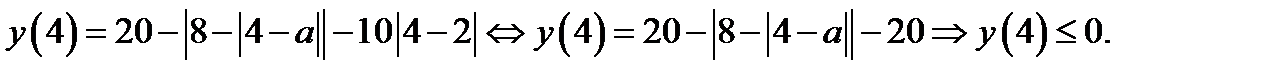
Так как точка 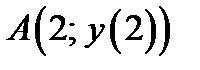 – точка максимума и
– точка максимума и 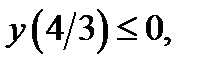
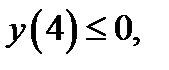 то исходное уравнение будет иметь хотя бы один корень тогда и только тогда, когда (рисунка 17)
то исходное уравнение будет иметь хотя бы один корень тогда и только тогда, когда (рисунка 17)
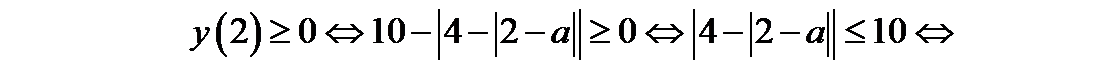
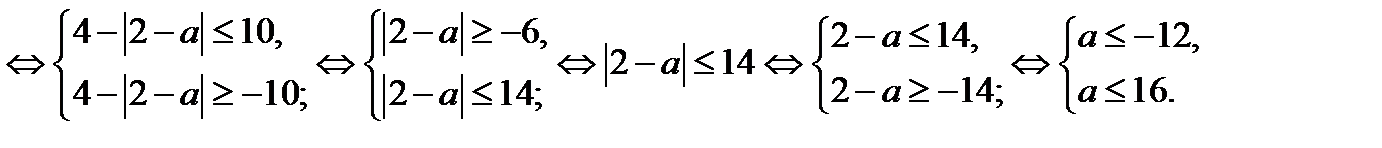 Исходное уравнение имеет хотя бы один корень, если
Исходное уравнение имеет хотя бы один корень, если 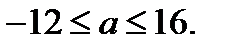
Ответ. 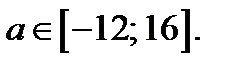
11.Решите уравнение 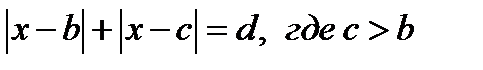 .
.
Решение. Рассмотрим функции 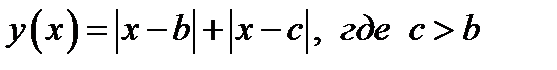 и
и 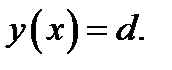
Построим график функции 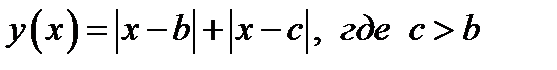 .
.
Имеем
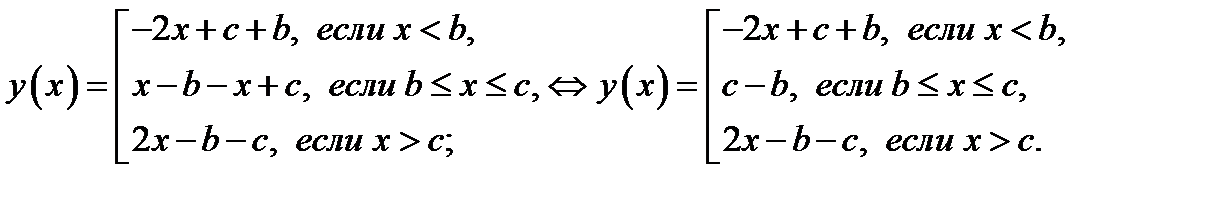
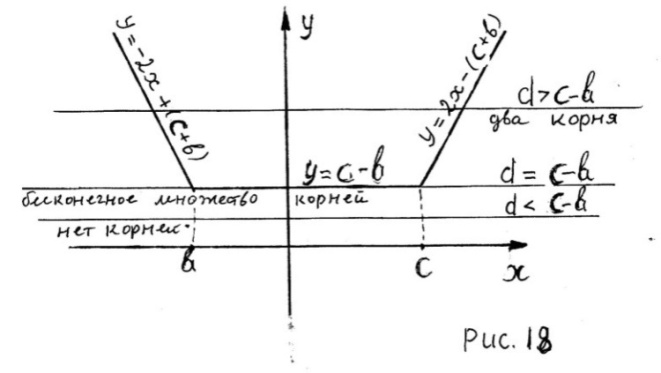
График функции 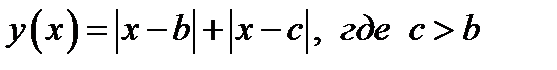 схематично изображён на рисунке 18.
схематично изображён на рисунке 18.
Число корней исходного уравнения при каждом значении d равно
количеству точек пересечения графиков функций 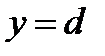 и
и 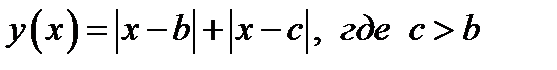 .
.  Корнями исходного уравнения являются абсциссы точек пересечения графиков функций
Корнями исходного уравнения являются абсциссы точек пересечения графиков функций 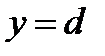 и
и 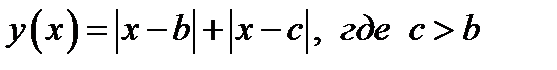 .
.
Из рисунка 18 следует, что исходное уравнение: а) не имеет корней, если 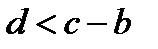 ; б) имеет бесконечное множество корней, (корнем является любое
; б) имеет бесконечное множество корней, (корнем является любое 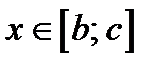 ), если
), если 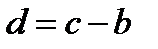 ; в) имеет два корня, если
; в) имеет два корня, если 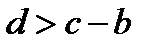 . Эти корни находятся из совокупности
. Эти корни находятся из совокупности
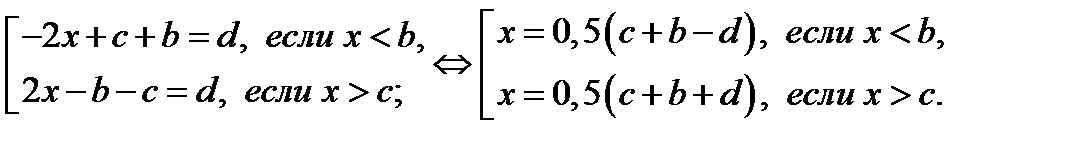
Итак, если 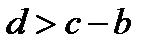 , то исходное уравнение имеет два корня:
, то исходное уравнение имеет два корня: 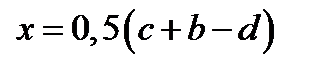 ,
, 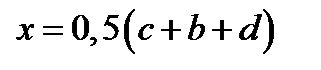 ;
;
Ответ. Если 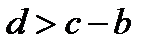 , то два корня
, то два корня 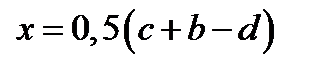 (корень меньше b),
(корень меньше b), 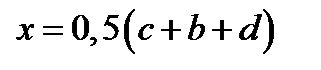 (корень больше с); если
(корень больше с); если 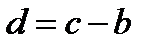 , то бесконечное множество корней, (корнем является любое
, то бесконечное множество корней, (корнем является любое 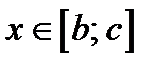 ); если
); если 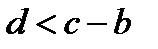 ,то не имеет корней.
,то не имеет корней.
12. Найдите все значения параметра а, при которых уравнение
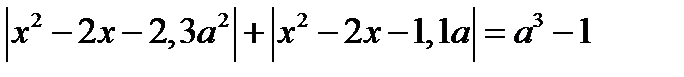 имеет четыре корня.
имеет четыре корня.
Решение. 1. Исходное уравнение равносильно уравнению
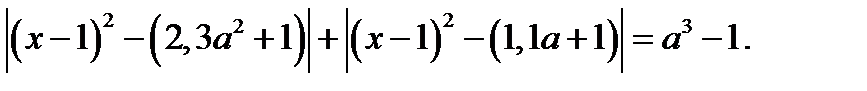
Сделаем замену 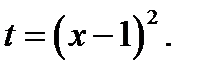 Очевидно,
Очевидно, 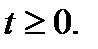
Исходное уравнение принимает вид
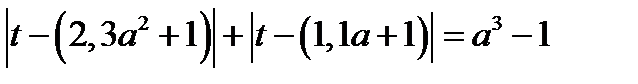 , где
, где 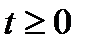 (12.1)
(12.1)
2. Рассмотрим квадратное уравнение 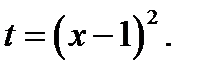 (12.2)
(12.2)
Если 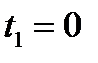 , то
, то 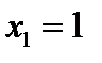 корень уравнения (12.2) кратности 2. Для
корень уравнения (12.2) кратности 2. Для
любого 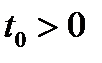 , уравнение (12.2) имеет два различных корня
, уравнение (12.2) имеет два различных корня 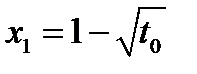
или 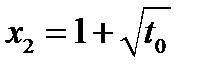 .
.
Исходное уравнение имеет четыре корня при тех значениях пара-
метра, при которых уравнение (12.1) имеет два положительных корня.
3. Рассмотрим уравнение (12.1).
1) Так как 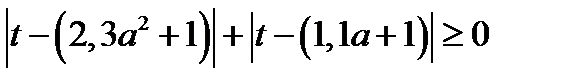 , то уравнение (12.1), а значит и исходное уравнение имеет решение, если
, то уравнение (12.1), а значит и исходное уравнение имеет решение, если 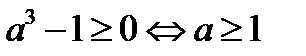 .
.
Если 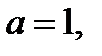 то уравнение (12.1) не имеет решений, так как оно принимает вид
то уравнение (12.1) не имеет решений, так как оно принимает вид 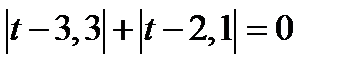 .
.
2) Пусть 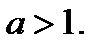 Обозначим:
Обозначим: 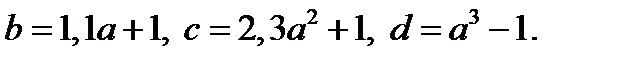 Тогда уравнение (12.1) принимает вид
Тогда уравнение (12.1) принимает вид 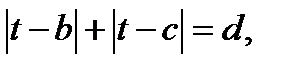 где
где 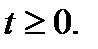 (12.3)
(12.3)
Очевидно, если 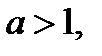 то
то 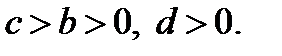
Уравнение (12.3) имеет два корня (задача 11), если 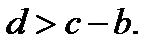 В этом случае числа
В этом случае числа 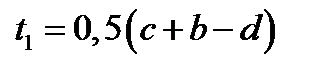 и
и 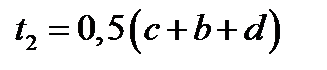 являются корнями уравнения (12.3) тогда и только тогда, когда
являются корнями уравнения (12.3) тогда и только тогда, когда 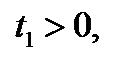
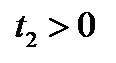 .
.
а) Число 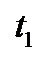 является корнем уравнения (12.3), если
является корнем уравнения (12.3), если
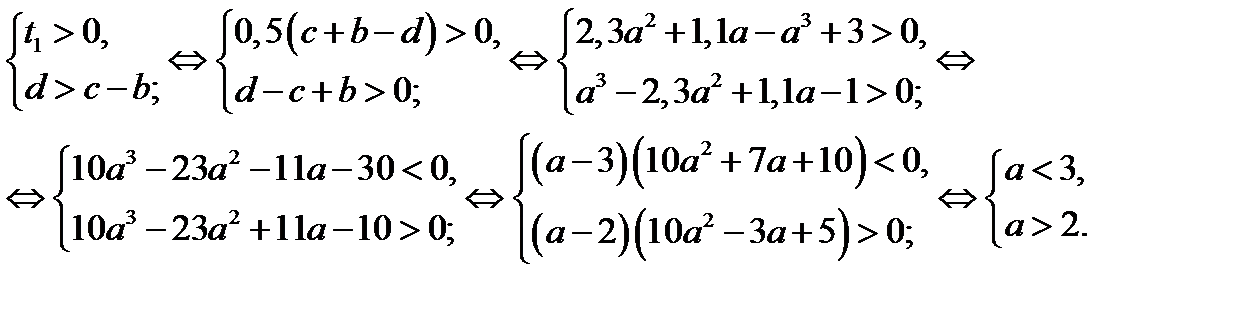
б) Так как 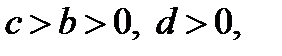 то
то 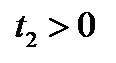 . Тогда
. Тогда 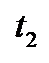 является корнем уравнения (12.3) при любом
является корнем уравнения (12.3) при любом 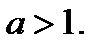
Итак, если 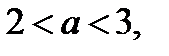 то уравнение (12.3) имеет два положительных корня, тогда исходное уравнение имеет четыре корня.
то уравнение (12.3) имеет два положительных корня, тогда исходное уравнение имеет четыре корня.
Ответ. 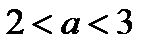 .
.
13.Найдите все значения параметров а и 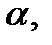 при которых уравнение
при которых уравнение 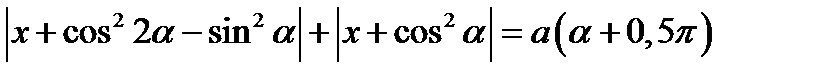 имеет единственный корень.
имеет единственный корень.
Решение. Обозначим: 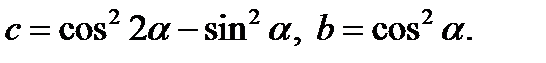 Тогда исходное уравнение принимает вид
Тогда исходное уравнение принимает вид 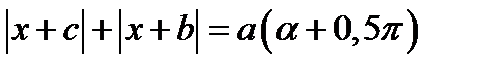 (13.1)
(13.1)
Уравнение (13.1), если 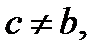 имеет, либо два корня, либо бесконечное множество корней, либо не имеет корней (задача 11). Поэтому уравнение (13.1), а значит и исходное уравнение может иметь единст-
имеет, либо два корня, либо бесконечное множество корней, либо не имеет корней (задача 11). Поэтому уравнение (13.1), а значит и исходное уравнение может иметь единст-
венный корень только в случае, если 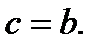
Если 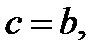 то уравнение (13.1) принимает вид
то уравнение (13.1) принимает вид
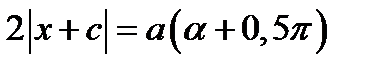 (13.2)
(13.2)
Последнее уравнение имеет единственное решение тогда и только тогда, когда 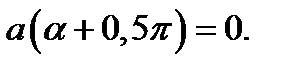
Итак, уравнение (13.2), а значит и исходное уравнение, имеет единственный корень тогда и только тогда, когда
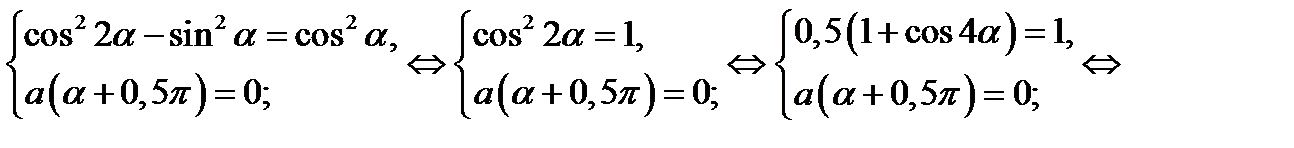
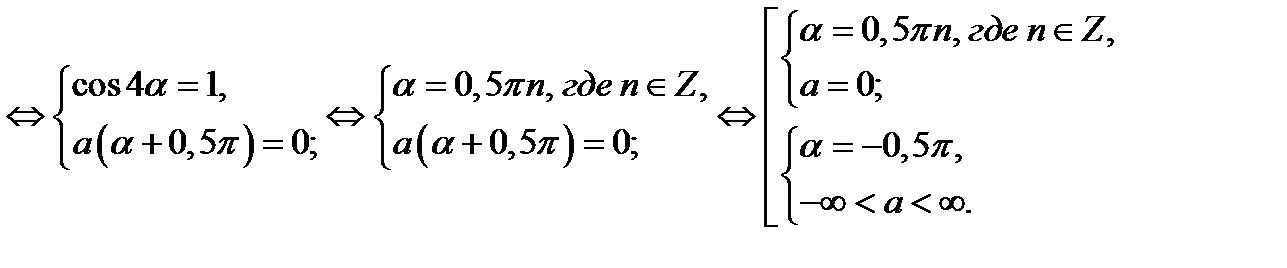
Из последней совокупности следует ответ.
Ответ. 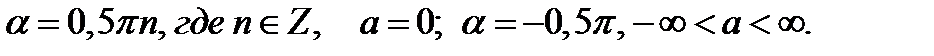
14. Найдите все значения параметра а, при которых уравнение 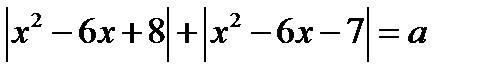 имеет три корня. Найдите эти корни.
имеет три корня. Найдите эти корни.
Решение. 1. Сделаем замену
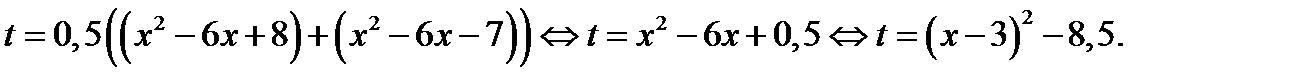
Так как 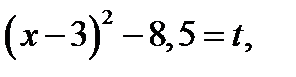 то
то 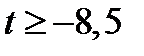 . (14.1)
. (14.1)
2. Рассмотрим квадратное уравнение (14.1).
Если 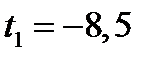 , то
, то 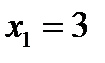 является корнем квадратного уравнения
является корнем квадратного уравнения
(14.1) кратности 2. Для любого 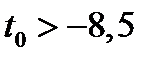 квадратное уравнение (14.1)
квадратное уравнение (14.1)
имеет два различных корня 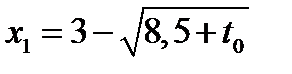 или
или 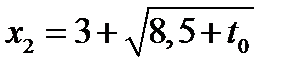 .
.
3. Если 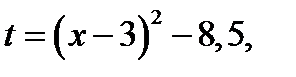 где
где 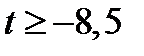 , то исходное уравнение принимает вид
, то исходное уравнение принимает вид 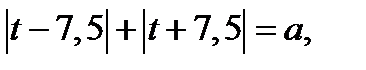 где
где 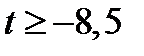 . (14.2)
. (14.2)
4. Из уравнения (14.2) следует, что 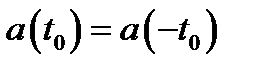 . Последнее равенство означает:при
. Последнее равенство означает:при 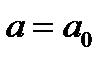 точки
точки 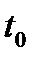 и
и 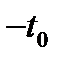 одновременно являются корнями уравнения (14.2).
одновременно являются корнями уравнения (14.2).
Из 2. и 4. следует, что исходное уравнение может иметь три корня только в случае, когда уравнение (14.2) имеет два корня, причём один из корней 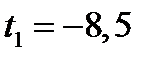 , а другой корень
, а другой корень 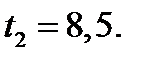
Из уравнения (14.2) следует, если 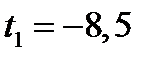 , то
, то 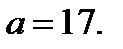
5. Имеем
если 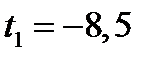 , то
, то 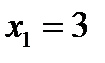 ;
;
если 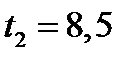 , то
, то 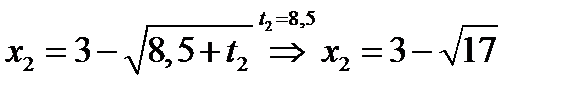 ,
, 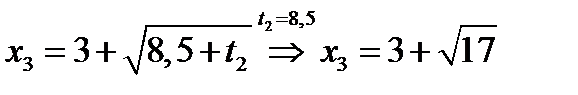 .
.
Ответ. Если 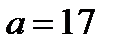 , то уравнение имеет три корня
, то уравнение имеет три корня 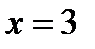 ,
, 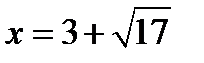 ,
, 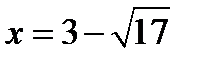 .
.
15. Найдите все значения параметра а, при которых уравнение 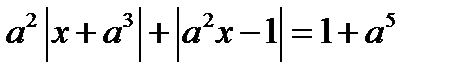 имеет не менее 7 корней, являющихся натуральными числами.
имеет не менее 7 корней, являющихся натуральными числами.
Решение. 1. Если  , то уравнение имеет бесконечное множество корней (уравнение принимает вид 1=1). Итак, при
, то уравнение имеет бесконечное множество корней (уравнение принимает вид 1=1). Итак, при  уравнение имеет не менее семи корней, являющихся натуральными числами.
уравнение имеет не менее семи корней, являющихся натуральными числами.
2. Если 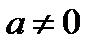 , то исходное уравнение равносильно уравнению
, то исходное уравнение равносильно уравнению
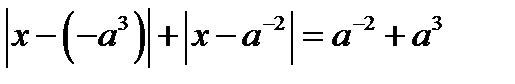 (15.1)
(15.1)
а) Так как 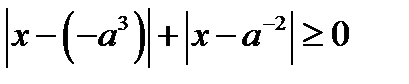 , то уравнение (15.1), а значит и исходное уравнение, имеет решение, если
, то уравнение (15.1), а значит и исходное уравнение, имеет решение, если
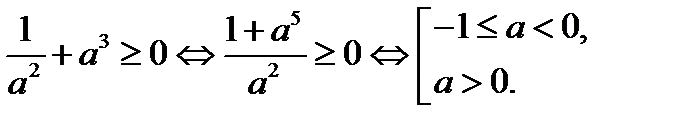 .
.
Итак, исходное уравнение имеет решение, если 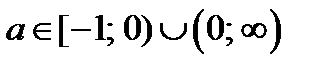 .
.
б) Если 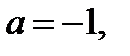 то исходное уравнение принимает вид
то исходное уравнение принимает вид
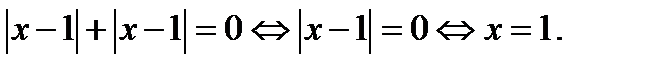
Последнее уравнение, а значит и исходное уравнение, если 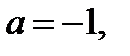 имеет единственный корень.
имеет единственный корень.
3. Рассмотрим уравнение (15.1), если 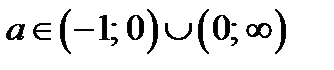 .
.
Обозначим: 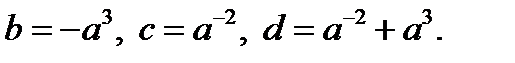 Очевидно,
Очевидно, 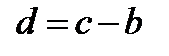 и так как
и так как 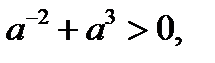 то
то 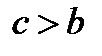 .
.
Уравнение (15.1) принимает вид 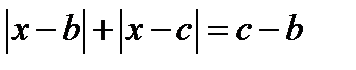 (15.2)
(15.2)
Уравнение (15.2), а значит и исходное уравнение, имеет бесконечное множество корней (задача 11). Корнем уравнения (15.2) является любое 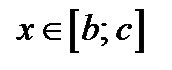 (задача 11). Тогда число корней уравнения (15.1), являющихся натуральными числами, совпадает с числом натуральных чисел отрезка
(задача 11). Тогда число корней уравнения (15.1), являющихся натуральными числами, совпадает с числом натуральных чисел отрезка 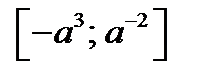 , где
, где 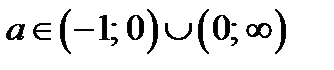 .
.
4. Рассмотрим все возможные случаи.
1) Если 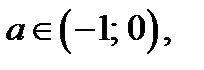 то
то 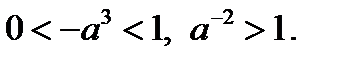 Отрезок
Отрезок 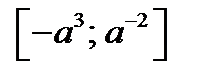 , где
, где
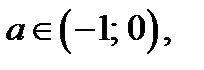 содержит не менее семи натуральных чисел (отрезку
содержит не менее семи натуральных чисел (отрезку
принадлежат числа 1, 2, …, 7, или 1, 2, …, 7, 8, или 1, 2, …, 7, 8, …), если
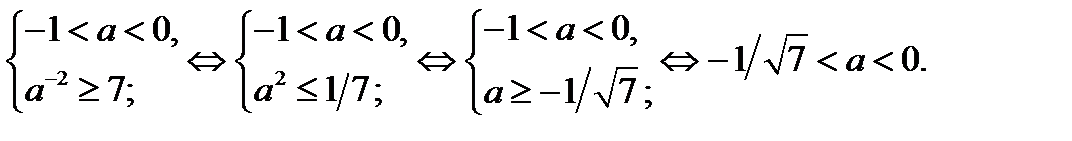
Исходное уравнение имеет не менее семи корней, являющихся натуральными числами, если 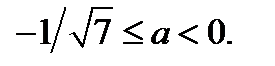
2) Если 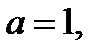 то исходное уравнение имеет корнем одно натуральное число (уравнение принимает вид
то исходное уравнение имеет корнем одно натуральное число (уравнение принимает вид 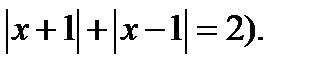
3) Если 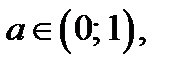 то
то 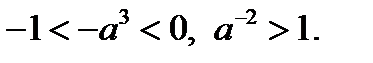 Отрезок
Отрезок 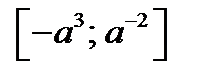 , где
, где 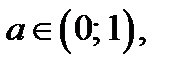 содержит не менее семи натуральных чисел (отрезку принадлежат числа 1, 2, …, 7, или 1, 2, …, 7, 8, или 1, 2, …, 7, 8, …), если
содержит не менее семи натуральных чисел (отрезку принадлежат числа 1, 2, …, 7, или 1, 2, …, 7, 8, или 1, 2, …, 7, 8, …), если
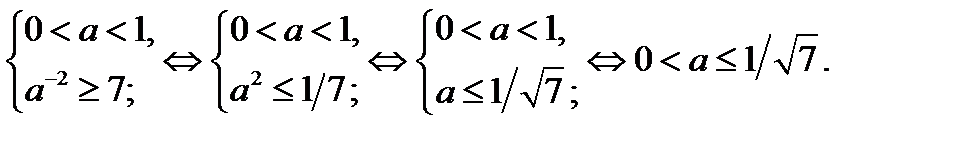
Исходное уравнение имеет не менее семи корней, являющихся натуральными числами, если 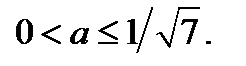
4) Если 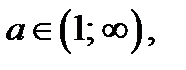 то
то 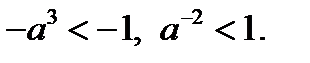 Отрезок
Отрезок 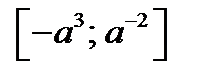 , где
, где 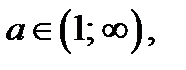 не содержит натуральных чисел.
не содержит натуральных чисел.
Ответ. 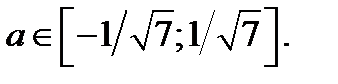
16. Найдите все значения параметра а, при которых уравнение
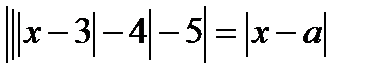 имеет 1) единственное решение, 2) два решения.
имеет 1) единственное решение, 2) два решения.
Решение. 1. На плоскости 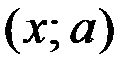 построим множество точек, удовлетворяющих уравнению
построим множество точек, удовлетворяющих уравнению 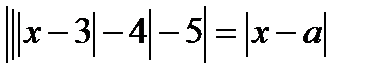 .
.
Для построения множества точек проделаем следующее.
Приравняем нулю выражение, стоящие под знаком модуля 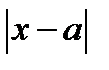 и получим уравнение
и получим уравнение 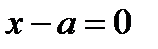 . Построим прямую
. Построим прямую 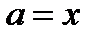 . Эта прямая разобьют плоскость
. Эта прямая разобьют плоскость 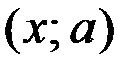 на 2 области. В области I выполняется неравенство
на 2 области. В области I выполняется неравенство 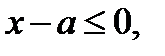 а в области II –
а в области II – 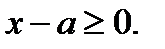
Рассмотрим исходное уравнение в каждой области.
2. В области I, где 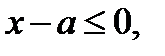 исходное уравнение равносильно уравнению
исходное уравнение равносильно уравнению 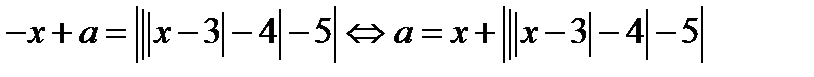 .
.
В области I построим множество точек, удовлетворяющих уравнению 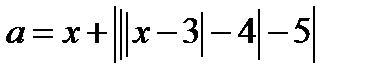 .
.
1) Найдём нули выражений, стоящих под модулями:
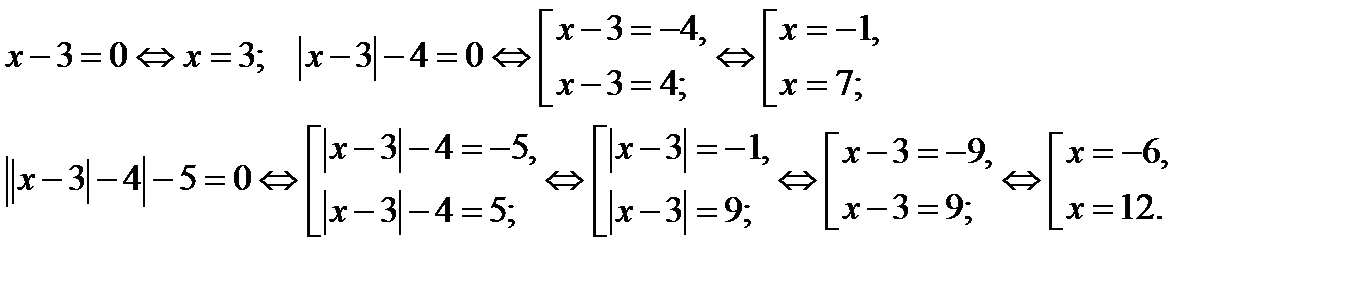
Итак, нули выражений, стоящих под модулями: 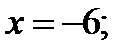
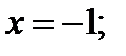
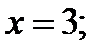
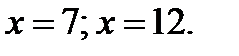
2) Так как функция 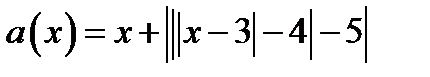 линейная на каждом промежутке
линейная на каждом промежутке 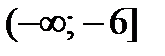 ,
, 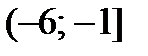 ,
, 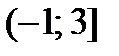 ,
, 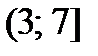 ,
, 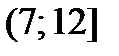 ,
, 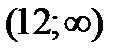 , то для того чтобы построить график функции
, то для того чтобы построить график функции 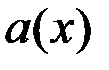 на каждом промежутке проделаем следующее.
на каждом промежутке проделаем следующее.
Найдём значения функции 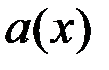 в точках
в точках 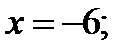
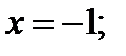
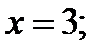
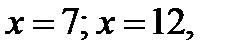 а также, например, в точках
а также, например, в точках 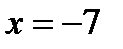 (принадлежит промежутку
(принадлежит промежутку 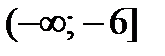 ) и
) и 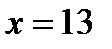 (принадлежит интервалу
(принадлежит интервалу 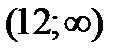 ). Имеем
). Имеем
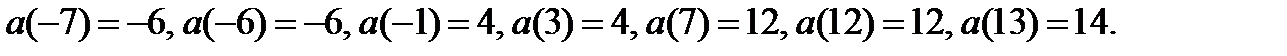 3) В области I построим точки:
3) В области I построим точки:
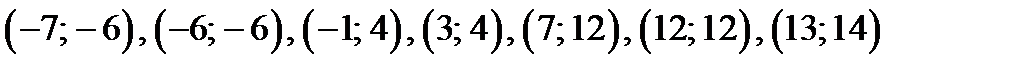 .
.
4) На каждом промежутке 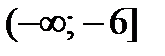 ,
, 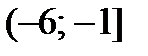 ,
, 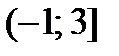 ,
, 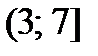 ,
, 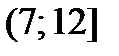 ,
, 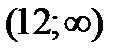 построим часть прямой, проходящей через точки абсциссы, которые принадлежат соответствующему промежутку.
построим часть прямой, проходящей через точки абсциссы, которые принадлежат соответствующему промежутку.
3. В области II, где 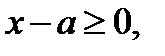 исходное уравнение равносильно
исходное уравнение равносильно
уравнению 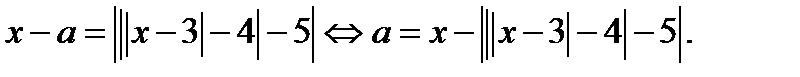
В области II построим множество точек, удовлетворяющих уравнению 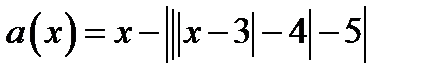 .
.
1) Нули выражений, стоящих под модулями: 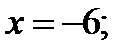
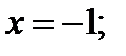
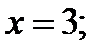
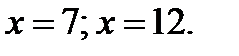
2) Так как функция 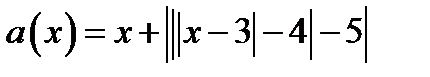 линейная на каждом промежутке
линейная на каждом промежутке 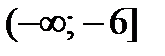 ,
, 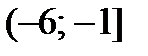 ,
, 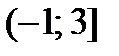 ,
, 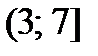 ,
, 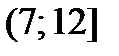 ,
, 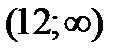 , то для того чтобы построить график функции
, то для того чтобы построить график функции 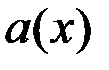 на каждом промежутке проделаем следующее.
на каждом промежутке проделаем следующее.
Найдём значения функции 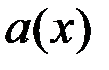 в точках
в точках 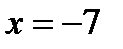 ;
; 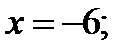
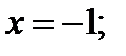
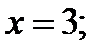
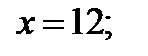
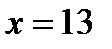 .
.
Имеем
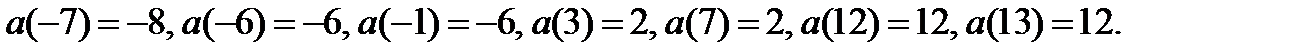
 3) В области II построим точки:
3) В области II построим точки:
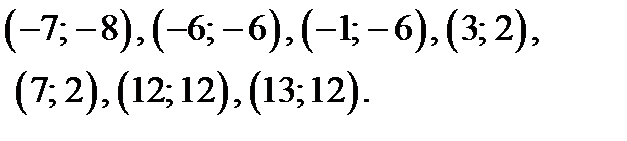
4) На каждом промежутке 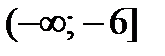 ,
, 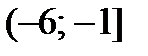 ,
, 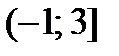 ,
, 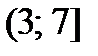 ,
, 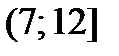 ,
, 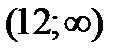 построим часть прямой, проходящей через точки абсциссы, которых принадлежат соответствующему промежутку.
построим часть прямой, проходящей через точки абсциссы, которых принадлежат соответствующему промежутку.
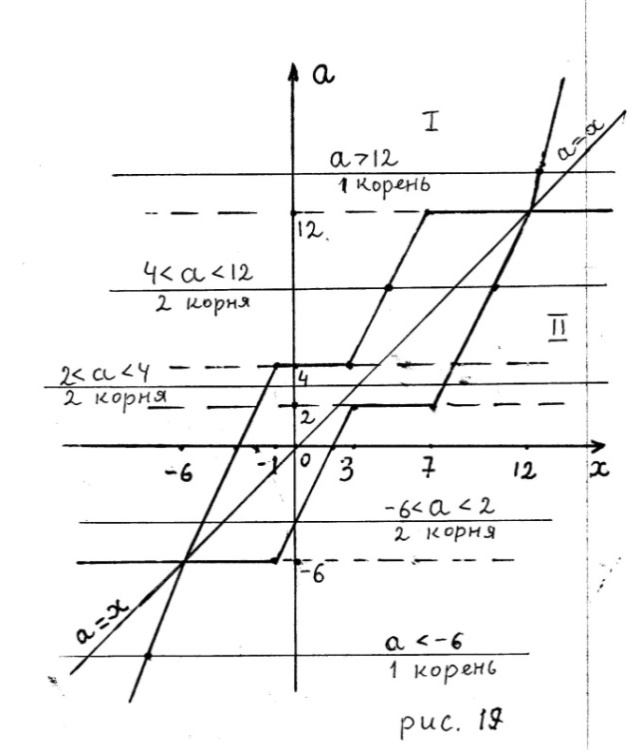
Из рисунка следует ответ.
Ответ. Единственное решение, если 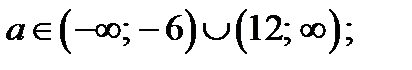 два решения, если
два решения, если 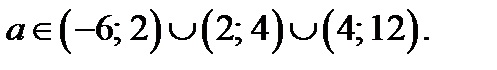
17. Найдите все значения параметра а, при которых уравнение 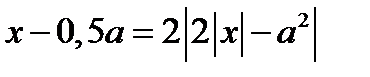 имеет 3 различных корня. Найдите эти корни.
имеет 3 различных корня. Найдите эти корни.
Решение. При 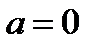 исходное уравнение имеет единственный корень:
исходное уравнение имеет единственный корень: 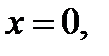 так как при
так как при 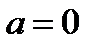 уравнение принимает вид
уравнение принимает вид 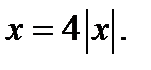
Пусть 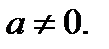
Рассмотрим функции 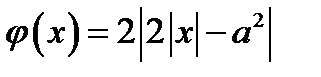 ,
, 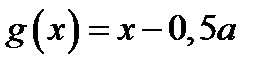 .
.
1. На плоскости 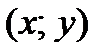 построим график функции
построим график функции 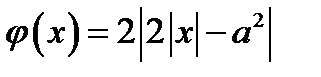 .
.
Так как функция 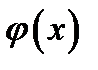 является чётной (так как
является чётной (так как 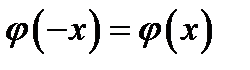 ), то график функции
), то график функции 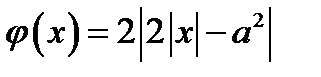 симметричен относительно оси у.
симметричен относительно оси у.
Построим график функции 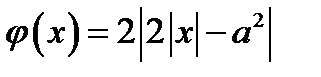 , если
, если 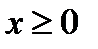 .
.
Если 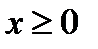 , то
, то 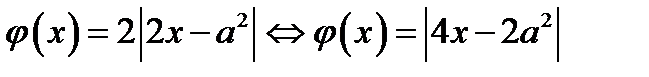 .
.
