Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

В этой статье мы разберем принципы решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами 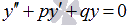, где p и q – произвольные действительные числа. Сначала остановимся на теории, далее применим полученные результаты в решении примеров и задач.

Если Вам будут встречаться незнакомые термины, то обращайтесь к разделу определения и понятия теории дифференциальных уравнений.

Сформулируем теорему, которая указывает, в каком виде находить общее решение ЛОДУ.

Теорема.

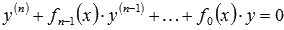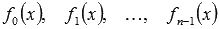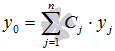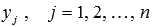Общее решение линейного однородного дифференциального уравнения с непрерывными на интервале интегрирования X коэффициентами определяется линейной комбинацией , где - линейно независимые частные решения ЛОДУ на X, а 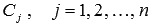- произвольные постоянные.

Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка 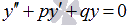с постоянными коэффициентами имеет вид y₀=C₁⋅y₁+C₂⋅y₂ , где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные. Осталось научиться находить частные решения y₁ и y₂.

Эйлер предложил искать частные решения в виде .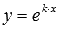

Если принять 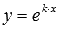частным решением ЛОДУ второго порядка с постоянными коэффициентами 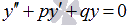, то при подстановке этого решения в уравнение мы должны получить тождество:

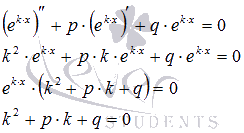
Так мы получили так называемое характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решения k₁ и k₂ этого характеристического уравнения определяют частные решения 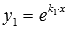и 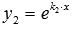нашего ЛОДУ второго порядка с постоянными коэффициентами.

В зависимости от коэффициентов p и q корни характеристического уравнения могут быть:

1. действительными и различными ,
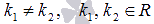2. действительными и совпадающими ,
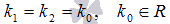3. комплексно сопряженной парой .

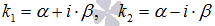В первом случае линейно независимыми частными решениями исходного дифференциального уравнения являются 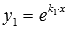и 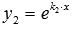, общее решение ЛОДУ второго порядка с постоянными коэффициентами есть .

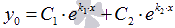Функци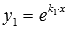и и 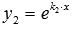действительно линейно независимы, так как определитель Вронского 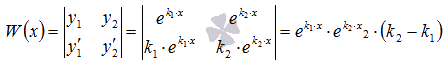отличен от нуля для любых действительных x при .

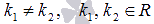Во втором случае одним частным решением является функция 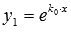. В качестве второго частного решения берется 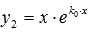. Покажем, что 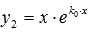действительно является частным решением ЛОДУ второго порядка с постоянными коэффициентами 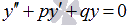и докажем линейную независимость y₁ и y₂.

Так как k₁ = k₀ и k₂ = k₀ совпадающие корни характеристического уравнения, то оно имеет вид 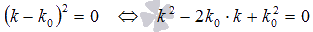. Следовательно, 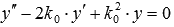- исходное линейное однородное дифференциальное уравнение. Подставим в него 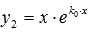и убедимся, что уравнение обращается в тождество:

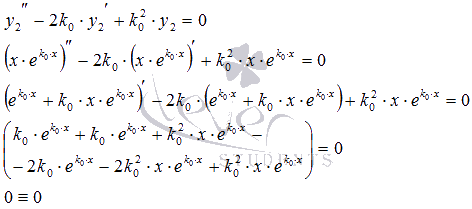
Таким образом, 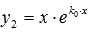является частным решением исходного уравнения.

Покажем линейную независимость функци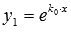й и 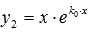. Для этого вычислим определитель Вронского и убедимся, что он отличен от нуля.

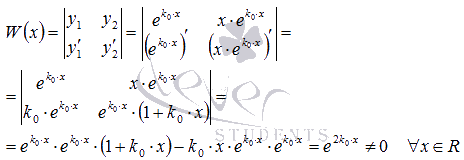
Вывод: линейно независимыми частными решениями ЛОДУ второго порядка с постоянными коэффициентами 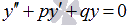являются 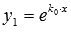и 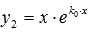, и общее решение есть 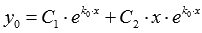при .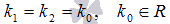

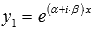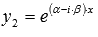В третьем случае имеем пару комплексных частных решений ЛОДУ и . Общее решение запишется как 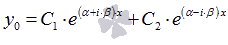. Эти частные решения могут быть заменены двумя действительными функциям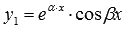и и 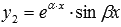, соответствующими действительной и мнимой частям. Это хорошо видно, если преобразовать общее решение 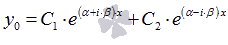, воспользовавшись формулами из теории функции комплексного переменного вида :

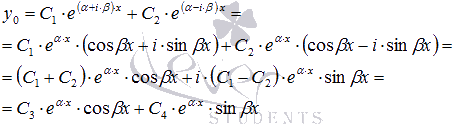
где С₃ и С₄ – произвольные постоянные.

Итак, обобщим теорию.