Синтетичний метод доведення нерівностей
Суть цього методу полягає в тому, що за допомогою певних перетворень нерівність, яку потрібно довести, виводять із деяких відомих (очевидних, або їх ще називають опорних) нерівностей. В ролі таких часто використовують нерівності:
а) 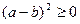 , б)
, б) 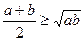 при
при 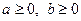 , в)
, в) 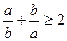 при
при 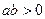 ,
,
г) 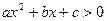 при
при 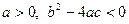 .
.
Логічна схема такого доведення виглядає у вигляді імплікацій
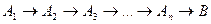 ,
,
де 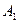 - деяка початкова вірна нерівність,
- деяка початкова вірна нерівність, 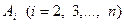 - отримані з неї вірні нерівності,
- отримані з неї вірні нерівності, 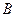 - нерівність, яку потрібно довести. Даний метод є достатньо ефективним, проте не завжди зрозуміло, з яких очевидних нерівностей потрібно розпочинати доведення. Відповідь на це питання іноді може дати аналітичний метод, який ми розглянемо у наступному пункті.
- нерівність, яку потрібно довести. Даний метод є достатньо ефективним, проте не завжди зрозуміло, з яких очевидних нерівностей потрібно розпочинати доведення. Відповідь на це питання іноді може дати аналітичний метод, який ми розглянемо у наступному пункті.
Наведемо приклади деяких доведень, де використовується синтетичний метод.
Задача 1.2.1. Довести, що для довільних 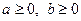 ,
, 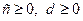 виконується нерівність
виконується нерівність
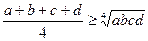 .
.
Доведення. Нам відомо, що при заданих обмеженнях на змінні виконуються нерівності 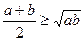 ,
, 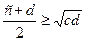 . Застосувавши нерівність Коші до лівих частин записаних нерівностей та використавши записані вище співвідношення, дістаємо
. Застосувавши нерівність Коші до лівих частин записаних нерівностей та використавши записані вище співвідношення, дістаємо
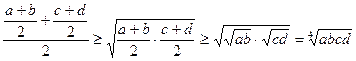 ,
,
або 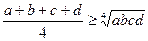 . Рівність можлива тоді і тільки тоді, коли одночасно виконуються умови
. Рівність можлива тоді і тільки тоді, коли одночасно виконуються умови 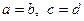 та
та 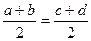 , тобто, коли
, тобто, коли 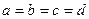 .
.
Задача 1.2.2. Довести, що 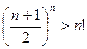 для
для 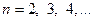 .
.
Доведення. Використаємо у ролі опорних наступні нерівності Коші:
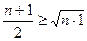 ,
, 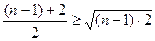 ,
, 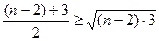 ,…,
,…,
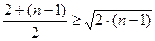 ,
, 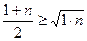 .
.
Перемноживши їх, дістаємо
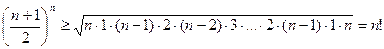 .
.
Оскільки у першій опорній нерівності при 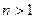 рівність неможлива, то остаточно отримуємо строгу нерівність, тобто, що
рівність неможлива, то остаточно отримуємо строгу нерівність, тобто, що 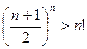 .
.
Задача 1.2.3. Довести, що при 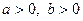 ,
, 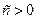 виконується нерівність
виконується нерівність
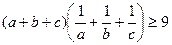 .
.
Доведення. Перший спосіб. Використаємо очевидні нерівності 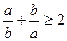 ,
, 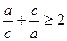 та
та 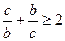 . Додавши їх, дістаємо
. Додавши їх, дістаємо 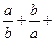
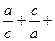
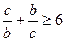 . Запишемо одержане співвідношення у виді
. Запишемо одержане співвідношення у виді
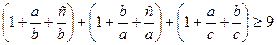 ,
,
або
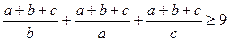 .
.
Винісши у лівій частині нерівності за дужки вираз 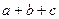 , отримуємо нерівність, яку потрібно було довести. Знак рівності виконується при
, отримуємо нерівність, яку потрібно було довести. Знак рівності виконується при 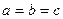 .
.
Другий спосіб. Використаємо розглянутий вище спосіб доведення нерівностей за допомогою означення. Для цього виконаємо наступні перетворення:
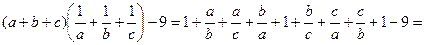
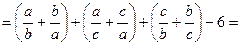
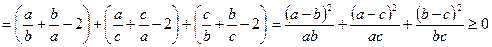 .
.
Отже, задана нерівність вірна.
Задача 1.2.4. Довести нерівність ( нерівність Коші – Буняковського)
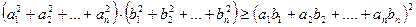 .
.
Доведення. Розглянемо очевидні нерівності
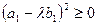 ,
, 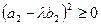 , ,
, , 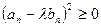 .
.
Додавши їх, отримаємо нерівність 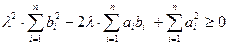 , яка виконується при довільному дійсному числі
, яка виконується при довільному дійсному числі 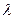 . Оскільки старший коефіцієнт
. Оскільки старший коефіцієнт 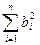 одержаного квадратного відносно
одержаного квадратного відносно 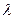 тричлена додатний, то його дискримінант не може бути додатним. Тому
тричлена додатний, то його дискримінант не може бути додатним. Тому
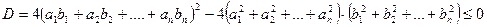 .
.
Звідси отримуємо потрібну нерівність.
Задача 1.2.5. Довести, що для довільних додатних чисел 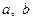 виконується нерівність
виконується нерівність 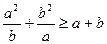 .
.
Доведення. Використаємо, як опорні, дві очевидні нерівності 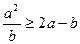 та
та 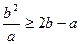 . Додаючи їх, отримуємо нерівність, яку потрібно було довести. Знак рівності виконується тільки у випадку, коли
. Додаючи їх, отримуємо нерівність, яку потрібно було довести. Знак рівності виконується тільки у випадку, коли 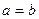 .
.
Задача 1.2.6. Довести, що для довільних дійсних чисел 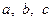 виконується нерівність
виконується нерівність 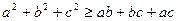 .
.
Доведення. Додавши очевидні нерівності 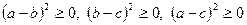 , отримуємо
, отримуємо
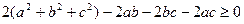 .
.
З одержаного співвідношення випливає нерівність, яку ми доводимо. Рівність виконується тільки у випадку 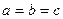 .
.
Задача 1.2.7. Довести, що при 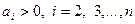 виконується нерівність
виконується нерівність
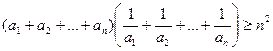 .
.
Доведення. Розглянемо очевидні нерівності
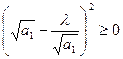 ,
, 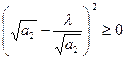 , ,
, , 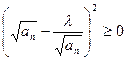 .
.
Додавши їх, отримаємо нерівність
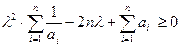 ,
,
яка виконується при довільному дійсному числі 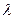 . Тому на дискримінант
. Тому на дискримінант 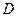 одержаного відносно
одержаного відносно 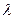 квадратного тричлена накладаємо умову
квадратного тричлена накладаємо умову
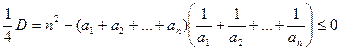 .
.
Звідси отримуємо потрібну нерівність. Дещо пізніше ми розглянемо інші способи доведення подібних нерівностей, зокрема із використанням скалярного добутку та його властивостей.
Задача 1.2.8. Довести, що для довільних додатних чисел 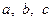 виконується нерівність
виконується нерівність
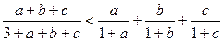 .
.
Розв’язання. Додавши три очевидні нерівності
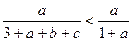 ,
, 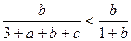 ,
, 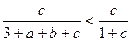 ,
,
отримуємо потрібну нерівність.
