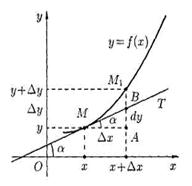
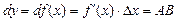Геометрический смысл дифференциала

Дифференциал функции

Справочный материал

1. Дифференциалом функции y=f(x) в точке хназывается главная часть еe приращения, равная произведению производной функции на приращение аргумента.

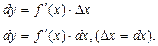
Применение дифференциала к приближенным вычислениям

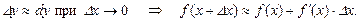
Основные теоремы о дифференциалах

Теорема 1. Пусть функции u=u(x), v=v(x) дифференцируемы, тогда

1⁰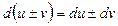

2⁰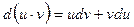

3⁰ .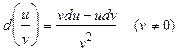

Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал промежуточного аргумента.

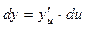, где у = у(u(х)) – сложная функция.

Инвариантность формы первого дифференциала

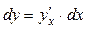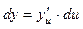или , где х – независимая переменная, u(х) – функция аргумента х.

Геометрический смысл дифференциала

Дифференциал функции y=f(x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение х