Бросают игральных костей. Найти метематическое ожидание числа таких бросаний, в каждом из которых выпадет ровно шестерок, если общее число бросаний равно . 3 страница
Таким образом, чтобы найти вероятность появления только одного из событий А1 и А2, достаточно найти вероятность появления одного, безразлично какого, из событий В1 и В2. События В1 и В2 несовместны, поэтому применима теорема сложения:
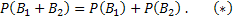
Остается найти вероятности каждого из событий В1 и В2. События А1 и А2 независимы, следовательно, независимы события А1 и 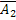 , а также
, а также 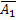 и А2, поэтому применима теорема умножения:
и А2, поэтому применима теорема умножения:
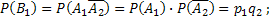
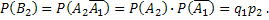
Подставив эти вероятности в соотношение (*), найдем искомую вероятность появления только оного из событий А1 и А2:
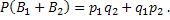
№50 Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того что при аварии сигнализатор сработает , равна 0.95 для первого сигнализатора и 0.9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
Решение:
Введем обозначения событий: 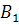 — появилось только событие
— появилось только событие 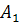 ( Срабатывание первого сигнализатора);
( Срабатывание первого сигнализатора); 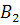 — появилось только событие
— появилось только событие 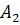 ( Срабатывание второго сигнализатора).
( Срабатывание второго сигнализатора).
Появление события 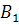 равносильно появлению события
равносильно появлению события 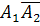 (появилось первое событие и не появилось второе), т. е.
(появилось первое событие и не появилось второе), т. е. 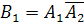 . Появление события
. Появление события 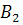 равносильно появлению события
равносильно появлению события 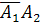 (появилось второе событие и не появилось первое), т. е.
(появилось второе событие и не появилось первое), т. е. 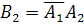 . Таким образом, чтобы найти вероятность появления только одного из событий
. Таким образом, чтобы найти вероятность появления только одного из событий 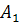 и
и 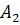 , достаточно найти вероятность появления одного, безразлично какого, из событий
, достаточно найти вероятность появления одного, безразлично какого, из событий 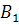 и
и 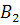 . События
. События 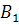 и
и 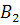 несовместны, поэтому применима теорема сложения:
несовместны, поэтому применима теорема сложения:
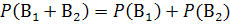
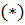
Остается найти вероятности каждого из событий 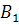 и
и 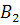 . События
. События 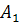 и
и 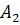 независимы, следовательно, независимы события
независимы, следовательно, независимы события 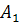 и
и 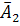 , а также
, а также 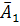 и
и 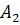 , поэтому применима теорема умножения:
, поэтому применима теорема умножения:


Подставив эти вероятности в соотношение 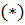 , найдем искомую вероятность появления только одного из событий
, найдем искомую вероятность появления только одного из событий 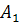 и
и 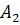 .
.

№51
Вероятность попадания при одном выстреле для первого стрелка равна 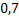 , значит вероятность промаха –
, значит вероятность промаха – 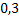 . Для второго –
. Для второго – 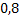 , а промаха –
, а промаха – 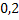 . Потому вероятность того, что при одном залпе в мишень попадет только один из стрелков
. Потому вероятность того, что при одном залпе в мишень попадет только один из стрелков 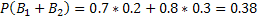 .
.
№52 Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.
Решение
Из данных задачи следует, что PA2=0,8; PB1+B2=0,38; где A1 и A2 – события попадания в цель первого и второго орудия соответственно. B1и B2 - попадание только одного из соответствующих орудий, т.е. B1 = A1*A2 и B2 = A2*A1 . Обозначим как PA1=p. Так как PB1+B2=PB1+ PB2, то подставляя, получим:
0,38=0,8-0,8p+0,2p.
p=0,7;
Вероятность поражения цели при одном выстреле первым из орудий составляет – 0,7.
№53
Обозначим за 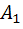 событие, что изделие 1 - стандартно
событие, что изделие 1 - стандартно
Обозначим за 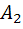 событие, что изделие 2 - стандартно
событие, что изделие 2 - стандартно
Событие Ā1 означает, что изделие 1 - нестандартно
Событие Ā2 означает, что изделие 2 - нестандартно
Тогда по теореме умножения вероятностей получаем, что вероятность того, что первое изделие стандартно, а второе – нет, равна 0,09
( 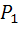 = P(
= P( 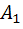 *Ā2)=P(
*Ā2)=P( 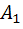 )*P(Ā2)=0.9*0.1=0.09)
)*P(Ā2)=0.9*0.1=0.09)
Соответственно вероятность обратного события (изделие 2 – стандартно, а изделие 1 - нестандартно) такая же
( 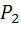 = P
= P 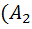 *Ā1)=P(
*Ā1)=P( 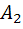 )*P(Ā1)=0.9*0.1=0.09)
)*P(Ā1)=0.9*0.1=0.09)
Тогда по теореме сложения вероятностей несовместных событий получаем, что вероятность того, что одно изделие стандартно, а другое – нет, равна 0,18
(P(( 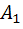 *Ā2)+
*Ā2)+ 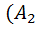 *Ā1))= P(
*Ā1))= P( 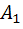 *Ā2)+ P
*Ā2)+ P 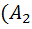 *Ā1)=
*Ā1)= 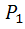 +
+ 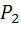 =0.09+0.09=0.18)
=0.09+0.09=0.18)
Ответ:0,18
№54 Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит точность.
Решение:
Обозначим допущение ошибки, превышающей заданную точность, в измерениях 1,2 и 3 как А1, А2 и А3 соответственно. Так как эти события независимы, то по теореме умножения вероятностей независимых событий искомая вероятность будет вычисляться по формуле:
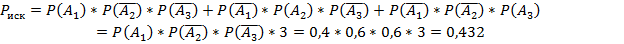
Ответ: 0,432.
Борисов Александр
№55 Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта.
Решение:
Обозначим появления товаров высшего сорта 1, 2 и 3 как А1, А2 и А3 соответственно. Так как эти события независимы, то по теореме умножения вероятностей независимых событий искомая вероятность будет вычисляться по формуле:
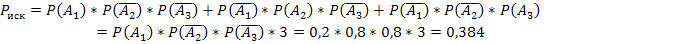
Ответ: 0,384.
№56 Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время работы t безотказно будут работать:
А) только один элемент;
Б) только два элемента;
В) все три элемента.
Решение.
Введем обозначение событий: безотказно работало первое устройство - A1; безотказно работало второе устройство - А2; безотказно работало третье устройство - A3.
B1 – безотказно работала за время t первое устройство A1; B2 – безотказно работало за время t второе устройство А2; B3 – безотказно работало за время t третье устройство A3.
а) Появление события B1 равносильно появлению события A1 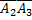 ;
; 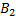 равносильно появлению события A2
равносильно появлению события A2 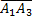 ;
; 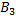 равносильно появлению A3
равносильно появлению A3 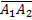 .
.
Таким образом, чтобы найти вероятность появления только одного из событий 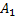 ,
, 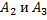 достаточно найти вероятность появления одного, безразлично какого, из событий
достаточно найти вероятность появления одного, безразлично какого, из событий 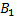 ,
, 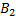 и
и 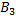 . События
. События 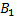 ,
, 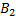 и
и 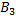 несовместы, поэтому применима теорема сложения:
несовместы, поэтому применима теорема сложения:
P ( 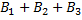 ) = P(
) = P( 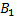 )+ P(
)+ P( 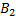 )+ P(
)+ P( 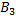 ). (*)
). (*)
Остается найти вероятности каждого из событий 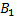 ,
, 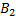 и
и 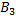 . События
. События 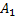 ,
, 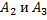 независимы, поэтому применима теорема умножения:
независимы, поэтому применима теорема умножения:
P ( 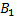 ) =P (A1
) =P (A1 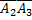 ) =
) = 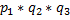 ;
;
P ( 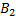 ) =P (A2
) =P (A2 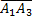 ) =
) = 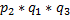 ;
;
P ( 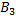 ) =P (A3
) =P (A3 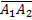 ) =
) = 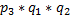 .
.
Подставив эти вероятности в соотношение (*), найдем искомую вероятность появления только одного из событий 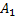 ,
, 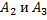 :
:
P ( 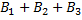 ) =
) = 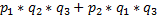 +
+ 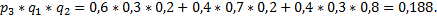
Б) Появление события B1 равносильно появлению события A1 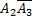 ;
; 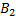 равносильно появлению события A1
равносильно появлению события A1 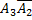 ;
; 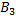 равносильно появлению A3
равносильно появлению A3 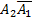 .
.
Аналогично предыдущему решению:
P ( 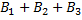 ) =
) = 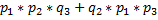 +
+ 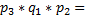 0,6*0,7*0,2+0,6*0,3*0,8+0,4*0,7*0,8=0,452.
0,6*0,7*0,2+0,6*0,3*0,8+0,4*0,7*0,8=0,452.
В) Пусть 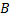 - безотказная работа всех устройств. Тогда событие B равносильно появлению
- безотказная работа всех устройств. Тогда событие B равносильно появлению 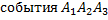 , поэтому P(B)=P(
, поэтому P(B)=P( 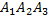 )=
)= 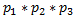 =0,6*0,7*0,8=0,336.
=0,6*0,7*0,8=0,336.
№57 Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвёртом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трёх ящиках; б) не менее чем в двух ящиках.
Решение.
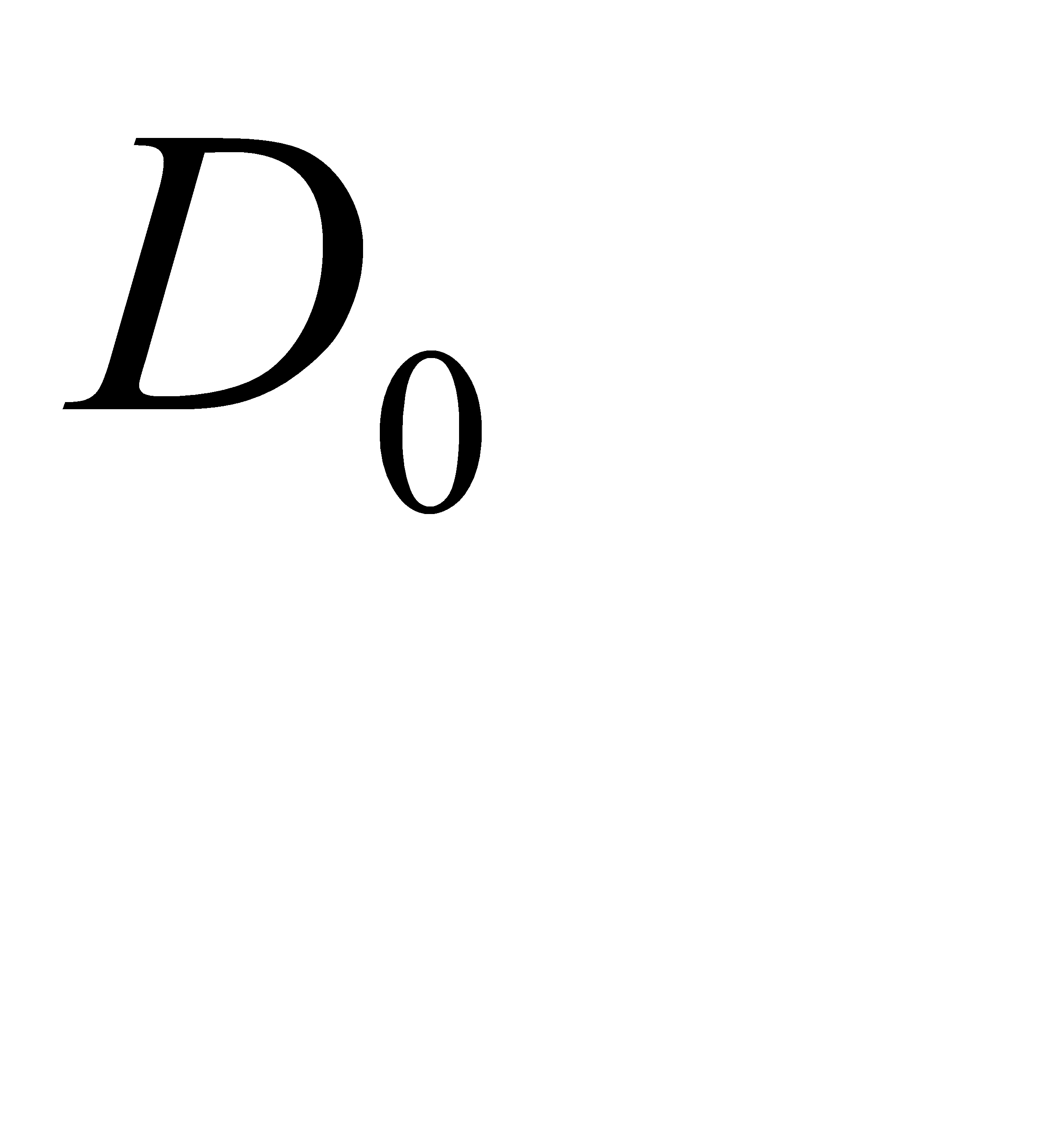 - детали нет ни в одном из ящиков,
- детали нет ни в одном из ящиков, 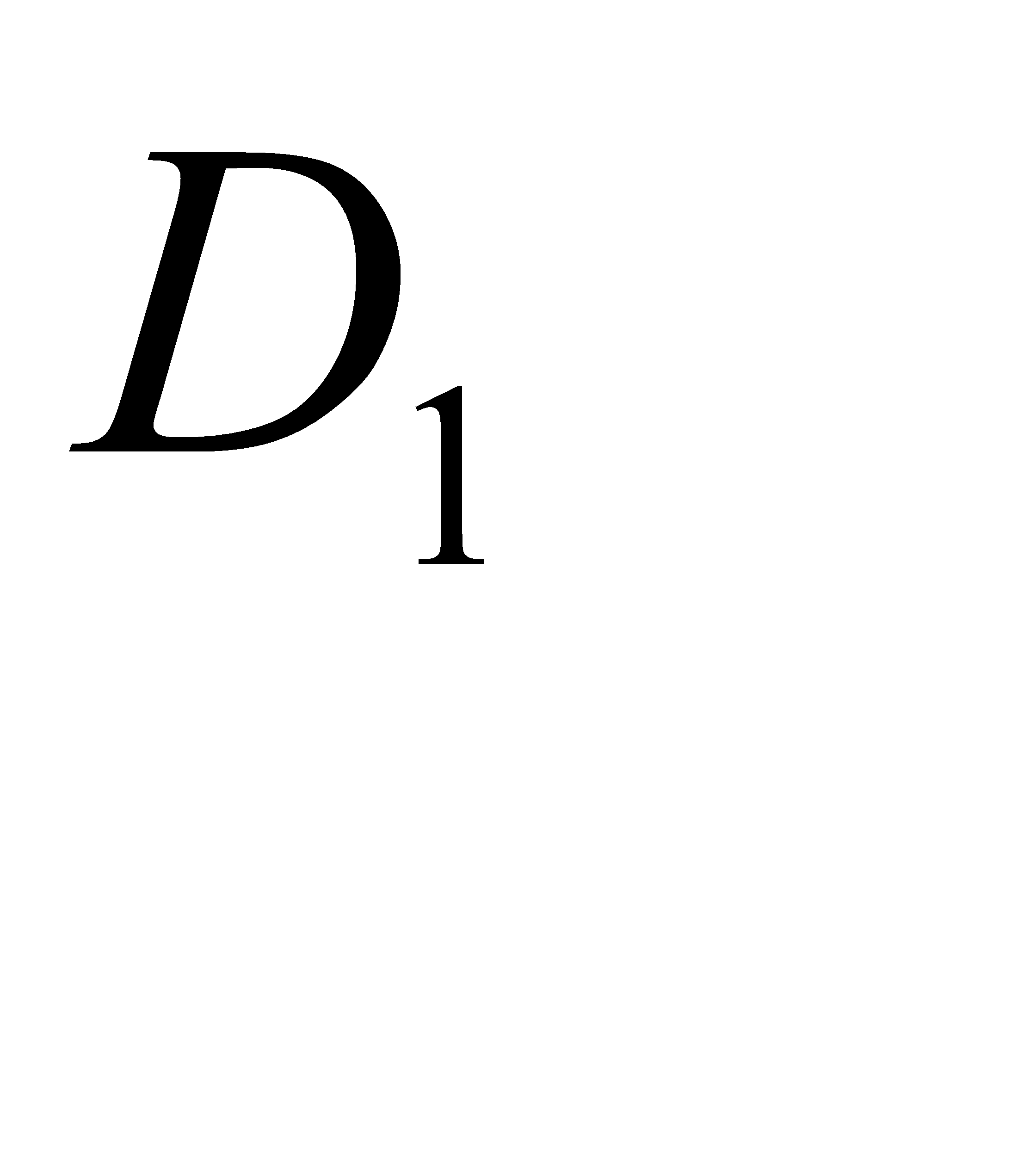 - деталь содержится в одном ящике,
- деталь содержится в одном ящике, 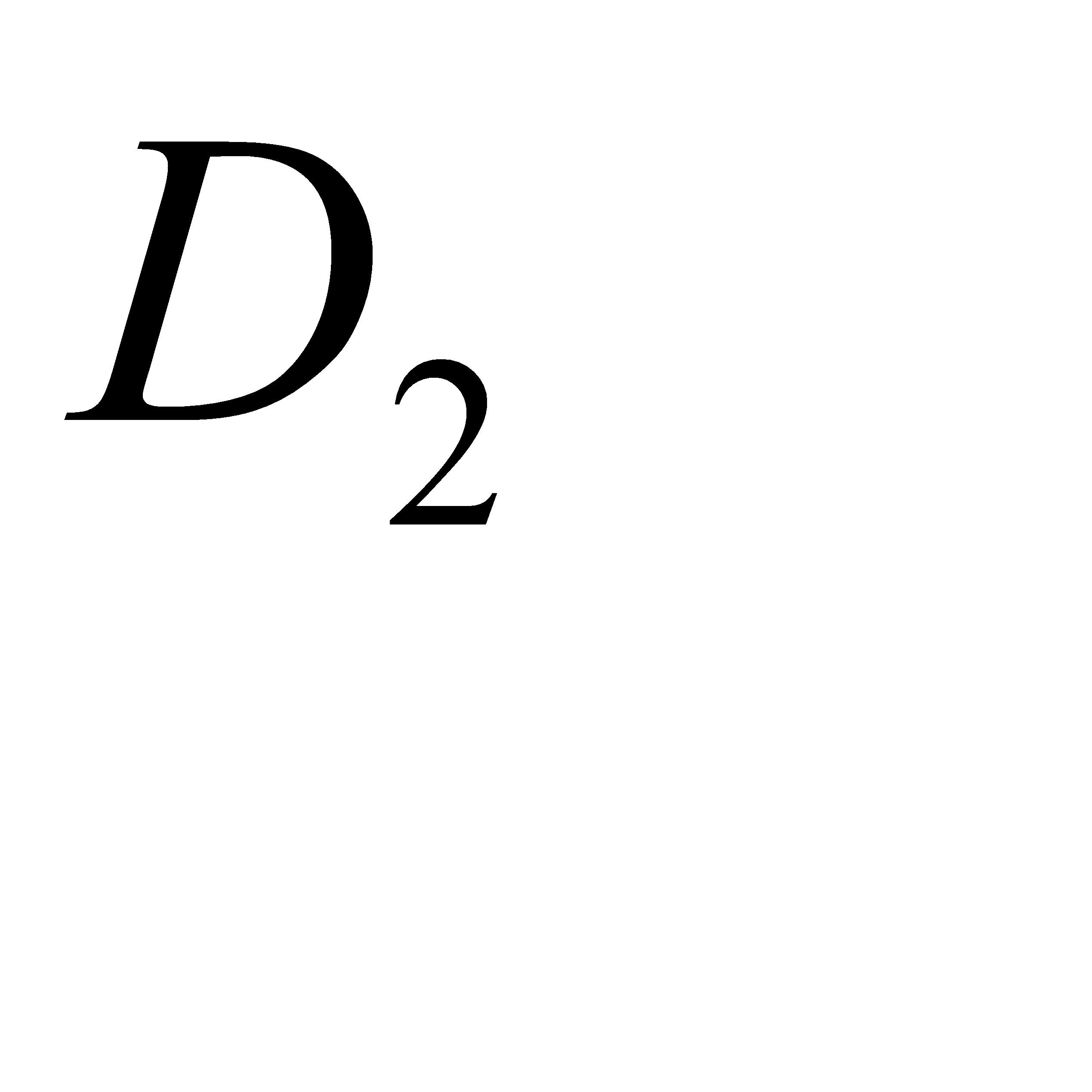 - в двух,
- в двух, 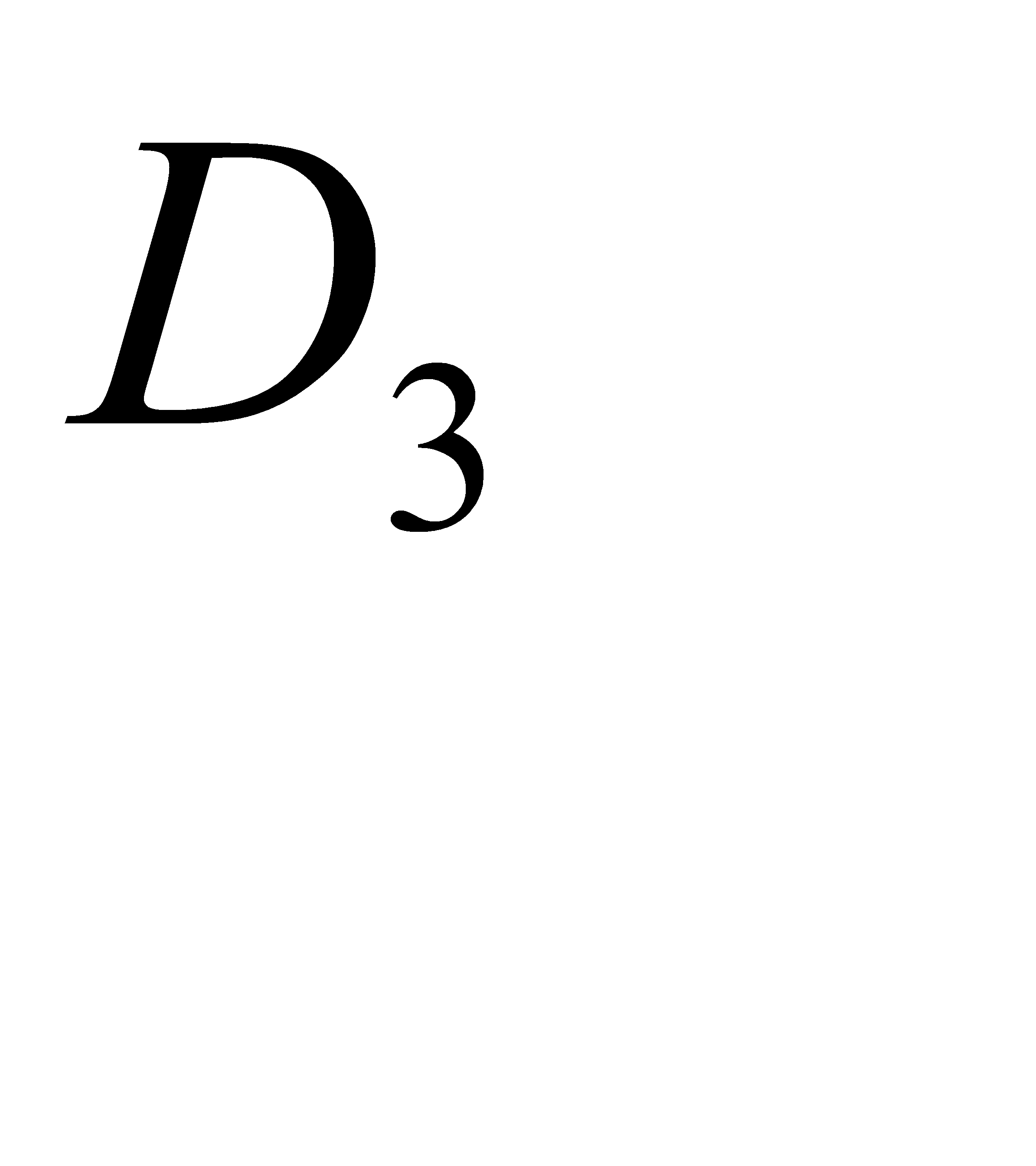 - в трёх,
- в трёх, 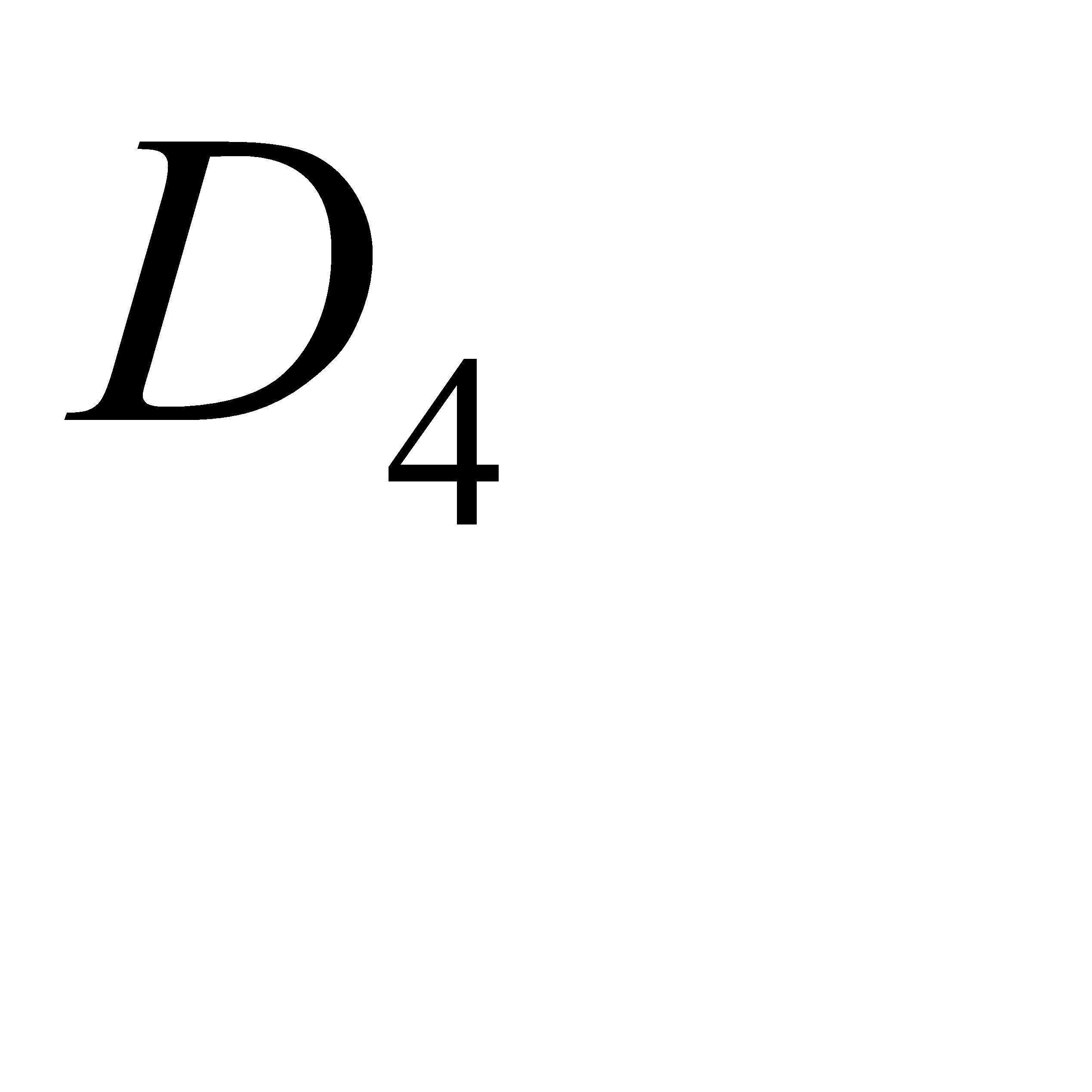 - в четырёх. Эти события несовместны и образуют полную группу, поэтому
- в четырёх. Эти события несовместны и образуют полную группу, поэтому 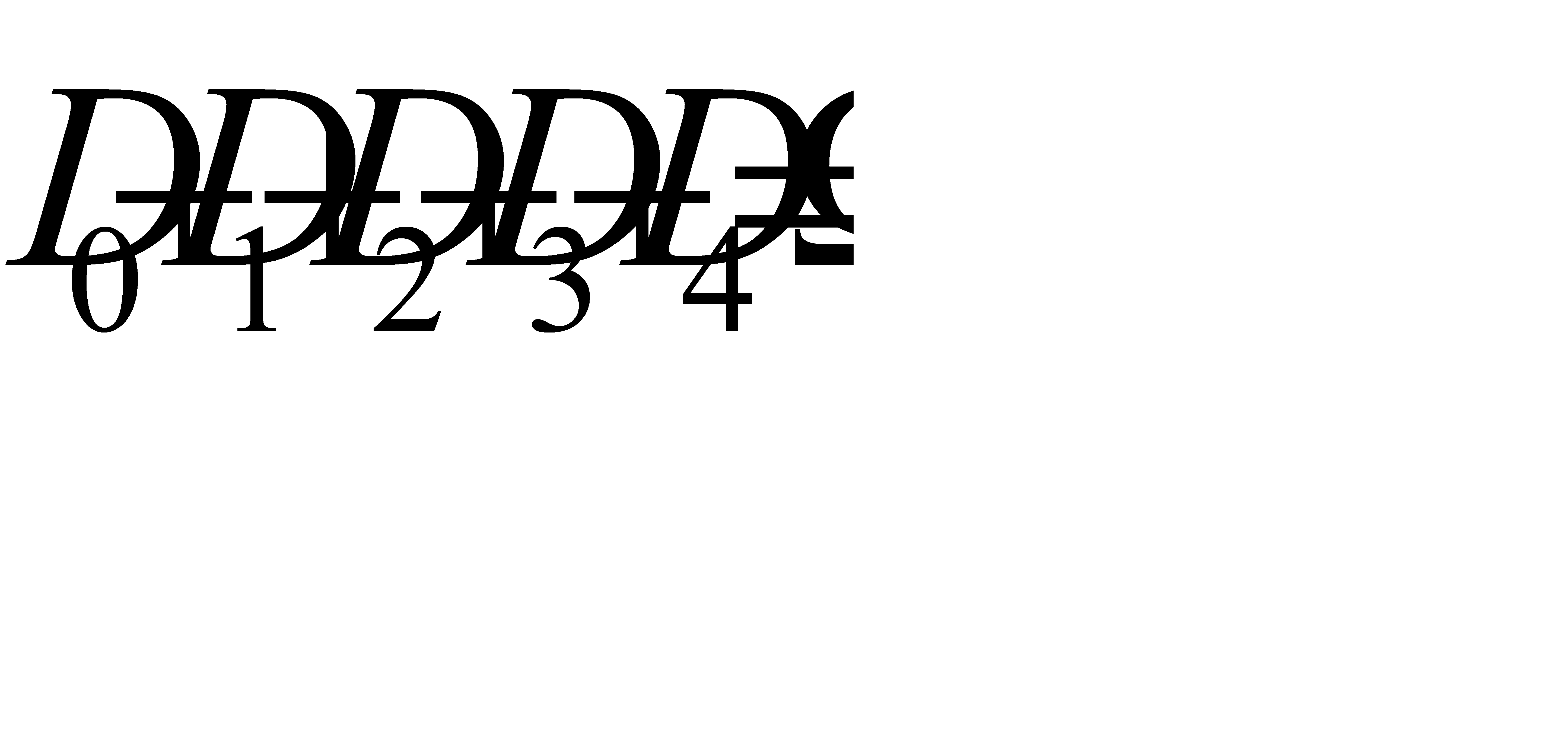 .
.
а) 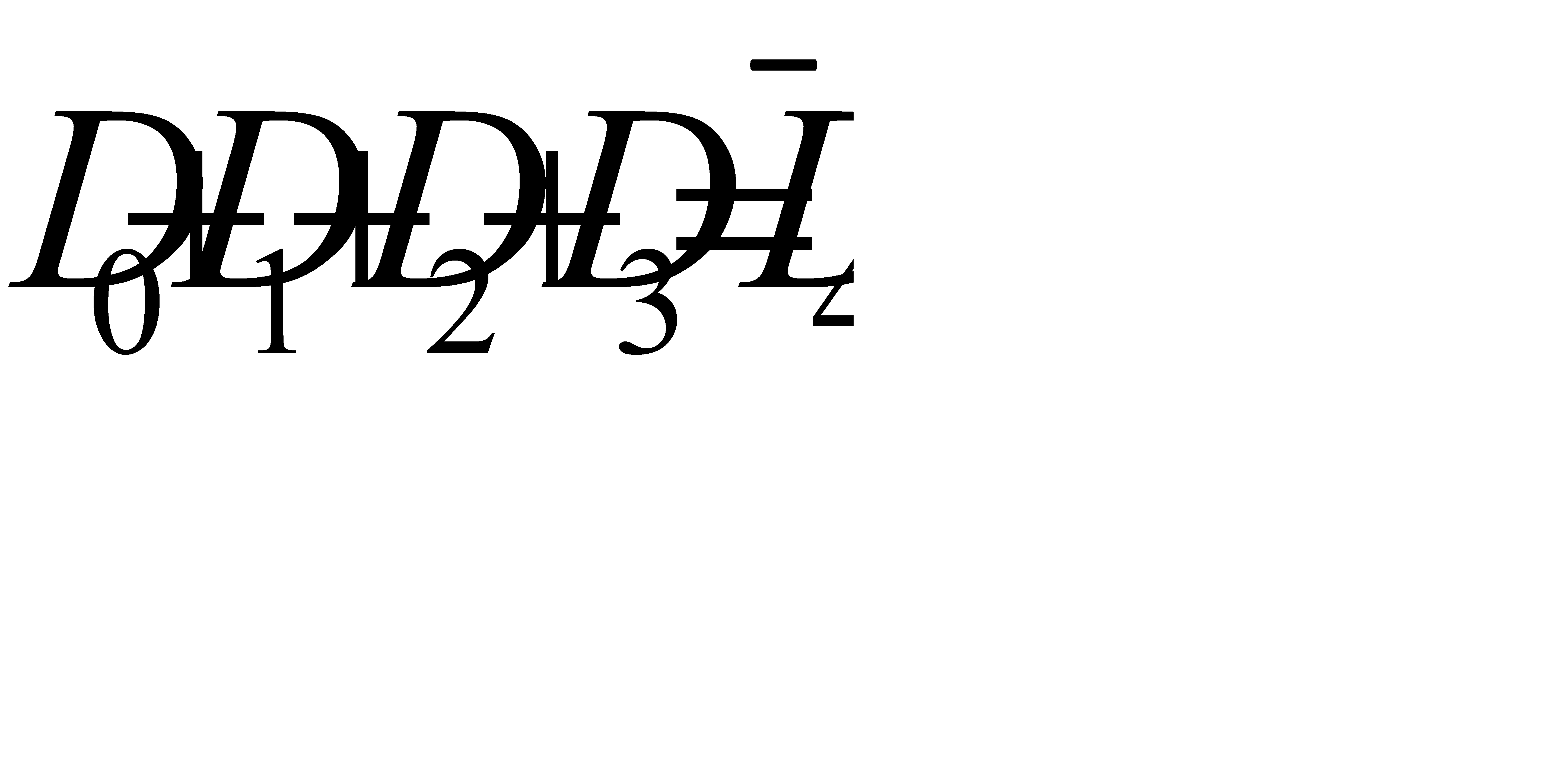 .
.
Искомая вероятность равна вероятности того, что деталь содержится не во всех четырёх ящиках.  .
.
б) 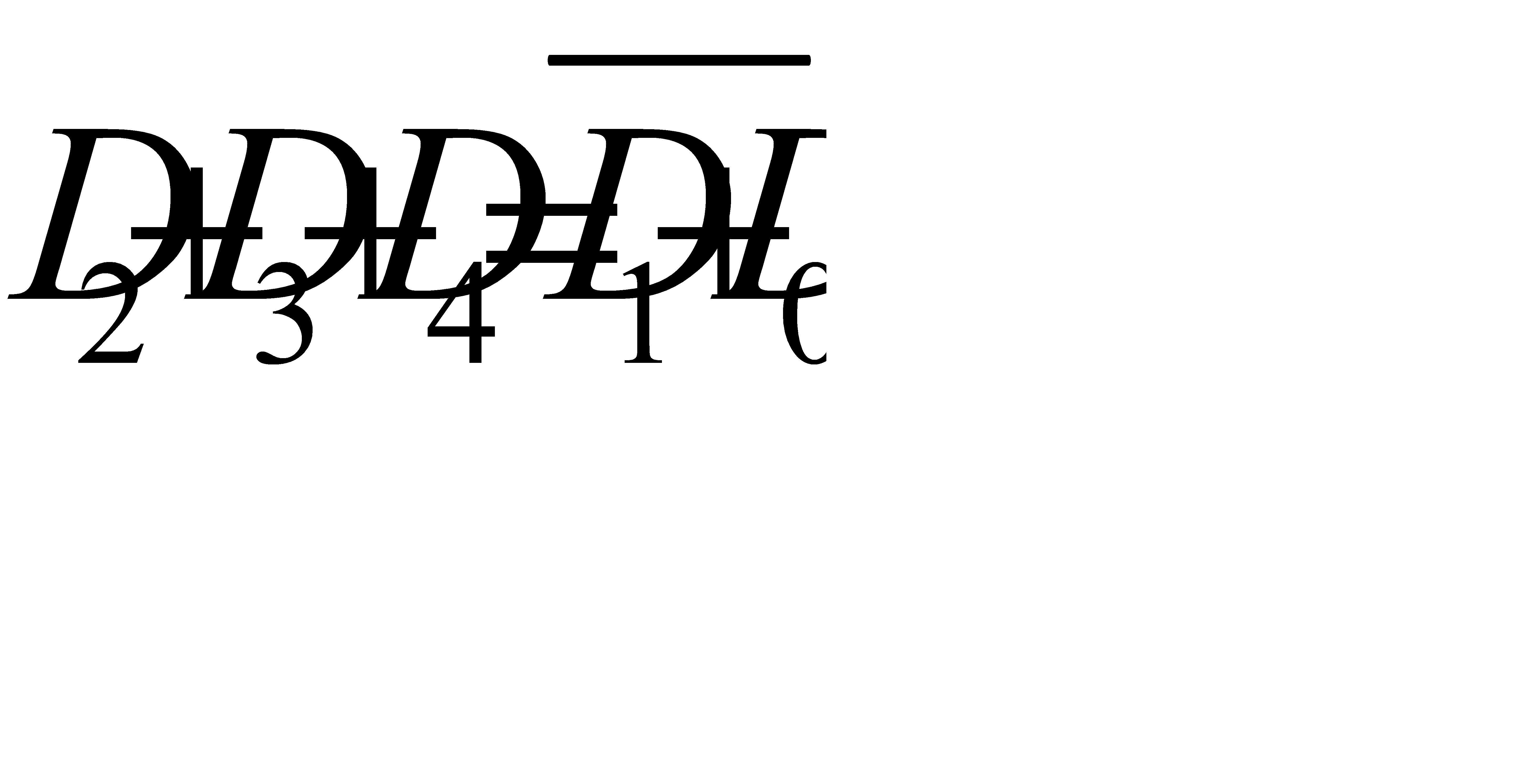 .
.

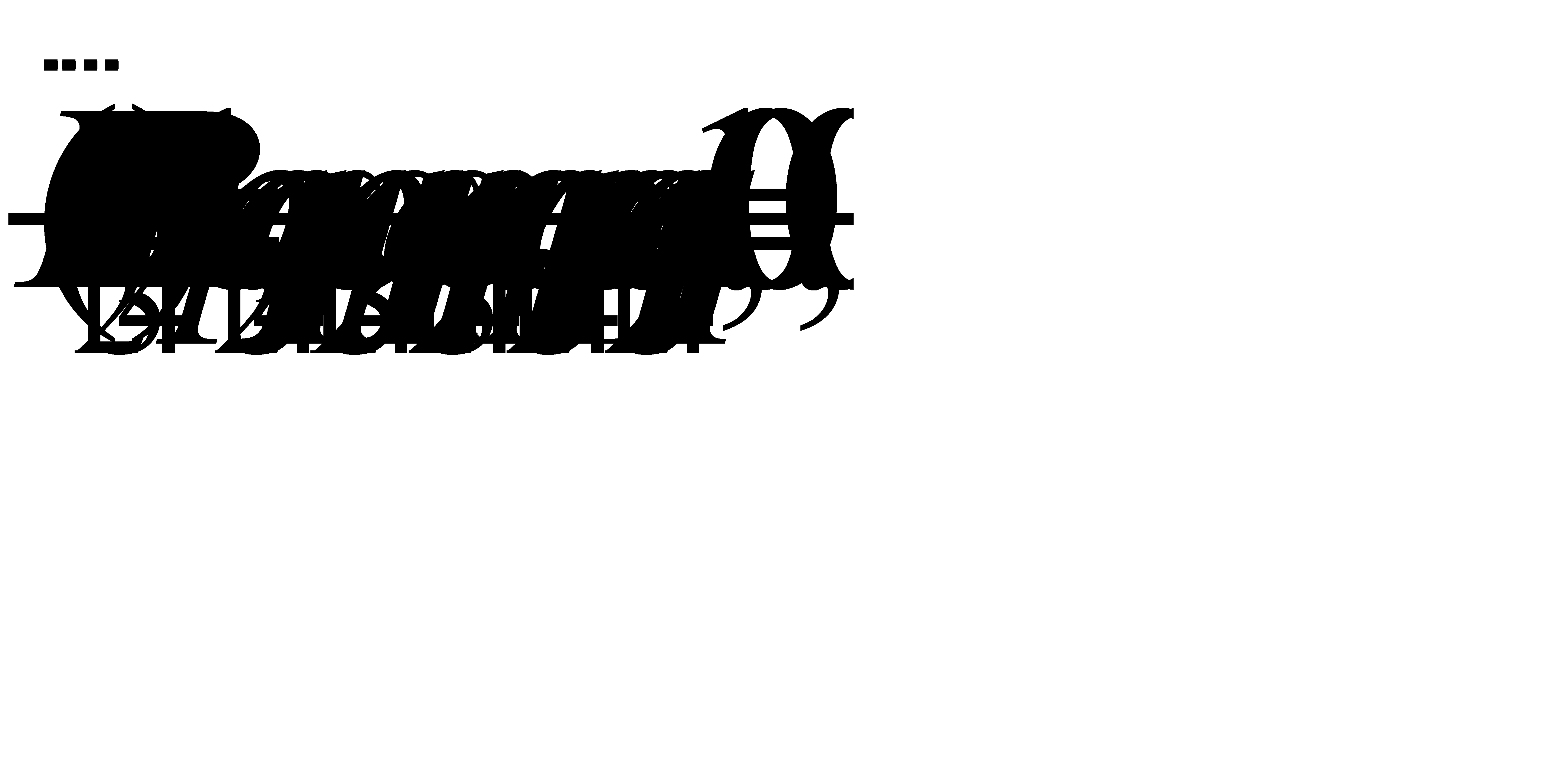
 .
.
№58 Брошены три игральные кости. Найти вероятность следующих событий: а) На каждой из выпавших граней появиться пять очков; б) на всех выпавших гранях появиться одинаковое число очков.
Решение:
а) Вероятность выпадения на одной игральной кости пяти очков равна p=1/6 .Тогда вероятность совместного появления 3 одинаковых событий равна P(A)=p*p*p=1/216.
б) Из первого решения видно, что вероятность появления на каждой из 3 граней одного определенного очка равна P(A)=p*p*p=1/216. Так как таких вариантов 6 ( по числу граней кости), то вероятность появления одинаковых очков равна P(B)=6*P(A)=6*1/216=1/36.
№59 Брошены три игральные кости. Найти вероятности следующих событий: а) на двух выпавших гранях появится одно очко, а на третьей грани – другое число очков; б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани – другое число очков; в) на всех выпавших гранях появится разное число очков.
Решение.
а) Вероятность того, что на выпавших двух гранях появится одно очко, равна 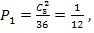 а вероятность того, что на другой грани появится другое количество очков, равна
а вероятность того, что на другой грани появится другое количество очков, равна 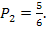
Искомую вероятность найдем по теореме умножения вероятностей: 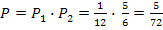 .
.
б) Вероятность того, что на некоторых двух гранях выпадет одинаковое число очков, равна 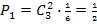 , а вероятность того, что на третьей грани выпадет другое число очков, равна
, а вероятность того, что на третьей грани выпадет другое число очков, равна 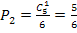 . Искомую вероятность найдем по теореме умножения вероятностей
. Искомую вероятность найдем по теореме умножения вероятностей 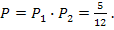
в) Количество благоприятствующих исходов равно 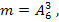 общее количество элементарных исходов равно
общее количество элементарных исходов равно 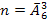 , искомая вероятность равна:
, искомая вероятность равна: 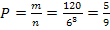 .
.
№60 Сколько надо бросить игральных костей, чтобы с вероятностью, меньшей 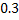 , можно было ожидать, что ни на одной из выпавших граней не появится шесть очков?
, можно было ожидать, что ни на одной из выпавших граней не появится шесть очков?
Решение:
Введем обозначения событий: 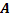 - ни на одной из выпавших граней не появится 6 очков;
- ни на одной из выпавших граней не появится 6 очков; 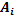 – на выпавшей грани
– на выпавшей грани 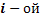 кости
кости 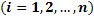 не появится 6 очков.
не появится 6 очков.
Интересующее нас событие 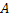 состоит в совмещении событий
состоит в совмещении событий 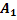 ,
, 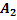 , …,
, …, 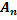 , т.е.
, т.е. 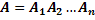
Вероятность того, что на любой выпавшей грани появится число очков, не равное шести, равна 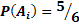
События 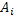 независимы в совокупности, поэтому применима теорема умножения:
независимы в совокупности, поэтому применима теорема умножения:
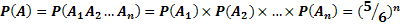
По условию, 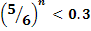 . Следовательно,
. Следовательно, 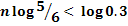 . Отсюда, учитывая, что
. Отсюда, учитывая, что 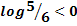 , найдем:
, найдем: 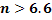 . Таким образом, искомое число игральных костей
. Таким образом, искомое число игральных костей 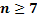
№61 Вероятность попадания в мишень стрелком при одном выстреле равна 0.8. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью, меньшей 0.4, можно было ожидать, что не будет ни одного промаха?
Решение:
Введем обозначения событий:
A – не произойдет ни одного промаха.
Ai – i-ым выстрелом стрелок не промахнется. i 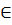 [1,n]
[1,n]
Очевидно, что A=A1A2…An
P(Ai)=0.8=4/5
События Ai независимы в совокупности, поэтому применима теорема умножения: P(A)=P(A=A1A2…An)=P(A1)P(A2)…P(An)=(4/5)n
(4/5)n<0.4=2/5
nlog4/5<log2/5 => n 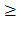 5
5
Ответ: n 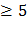 .
.
№62 В круг радиуса R вписан правильный треугольник. Внутрь круга наудачу брошены 4 точки. Найти вероятность следующих событий: a) все 4 точки внутрь треугольника; б) одна точка попадет внутрь треугольника и по одной точке попадет на каждый “малый” сегмент. Предполагается, что вероятность попадания точки в фигуру пропорциональна площади фигуры и не зависит от ее расположения.
Решение:
a) Введем обозначения событий:
P(Ai) – i-ая точка попадет в треугольник. i 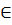 [1,4]
[1,4]
P(A) – искомое событие
P(A)=P(A1) P(A2) P(A3) P(A4)
Известно, что:
S1= 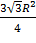 – площадь треугольника
– площадь треугольника
S2= 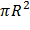 – площадь круга
– площадь круга
Тогда: P(Ai)= 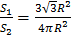 =
= 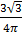
Отсюда получаем, что: P(A)= 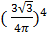
б) Введем обозначения событий:
P(B) – какая-то точка попадет в треугольник
P(Ai) – i-ая точка попадет в “малый” сегмент, i 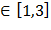
P(A)=P(A1) P(A2) P(A3) P(B)
Известно, что:
S1= 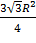 – площадь треугольника
– площадь треугольника
S2= 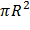 – площадь круга
– площадь круга
Тогда: P(B) = 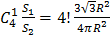 =
= 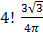
S3= 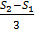
P(Ai)= 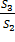 => P(Ai)=
=> P(Ai)= 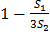
P(A) = 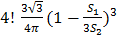
Ответ: a) 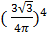 ; б)
; б) 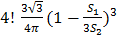
№63 Отрезок разделен на три равные части. На этот отрезок наудачу брошены три точки. Найти вероятность того, что на каждую из трех частей отрезка попадает по одной точке.
Решение:
Пусть
P(Ai) – вероятность того, что i-ая точка попадет на часть отрезка
P(A) – искомое событие
Т.к. на каждом отрезке должна быть только одна точка, то:
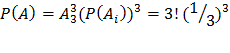
Ответ: 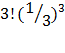
№64 В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
Решение:
Пусть
A – первый взятый учебник имеет переплет
B – второй взятый учебник имеет переплет
P(A)=3/6=1/2
PA(B)=(3-1)/(6-1)=2/5
P(AB)=P(A) PA(B)= 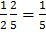
Ответ: 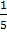
№65 Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными.
Решение:
A – первый билет выигрышный
B – второй билет выигрышный
P(A)=5/100=1/20
PA(B)=(5-1)/(100-1)=4/99
P(AB)=P(A) PA(B)= 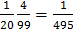
Ответ: 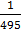
№66 В цехе работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение:
A – первым отобран мужчина
B – вторым отобран мужчина
С – третьим отобран мужчина
P(A)=7/10
PA(B)=(7-1)/(10-1)=6/9=2/3
PAB(C)=(7-2)/(10-2)=5/8
P(ABC)=P(A) PA(B) PAB(C)= 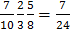
Ответ: 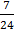
№67 В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлеченные детали являются окрашенными.
Решение:
A – первая деталь окрашенная
B – вторая деталь окрашенная
С – третья деталь окрашенная
D – четвертая деталь окрашенная
P(A)=6/10=3/5
PA(B)=(6-1)/(10-1)=5/9
PAB(C)=(6-2)/(10-2)=4/8=1/2
PABC(D)=(6-3)/(10-3)=3/7
P(ABCD)=P(A) PA(B) PAB(C) PABC(D)= 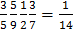
Ответ: 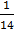
№68 В урне имеется 5 шаров с номерами от 1 до 5. Наудачу по одному извлекаются 3 шара без возвращения. Найти вероятность следующих событий: а) последовательно появятся шары с номерами 1, 4, 5; б) извлеченные шары будут иметь номера 1, 4, 5 независимо от того, в какой последовательности они появились.
Решение:
а) введем обозначение событий: А – выпал шар с номером 1, В – выпал шар с номером 4, С – выпал шар с номером 5. Вероятность наступления события А – Р(А) =  . Вероятность наступления события В при условии, что событие А уже наступило -
. Вероятность наступления события В при условии, что событие А уже наступило - 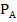 (В) =
(В) =  , вероятность события С при условии А, В -
, вероятность события С при условии А, В - 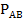 (С) =
(С) =  . Искомая вероятность того, что последовательно выпадут шары с номерами 1, 4, 5 по правилу умножения равна произведению вероятностей событий А, В, С : Р =
. Искомая вероятность того, что последовательно выпадут шары с номерами 1, 4, 5 по правилу умножения равна произведению вероятностей событий А, В, С : Р = 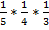 =
=  ≈ 0, 016
≈ 0, 016
