Двухфакторный дисперсионный анализ

Пусть случайная величина 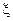зависит от двух признаков (факторов) 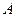и
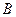
Обозначим 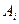, , 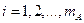, 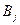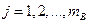— уровни факторов 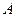и 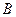, соответственно.
Результаты измерения случайной величины 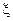представлены в таблице

				...
				...
				...
...	...	...	...	...	...
				...

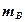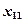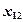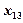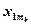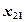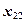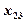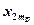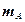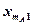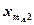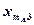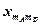В каждой клетке таблицы – при каждом сочетании уровней факторов проведено по одному наблюдению (измерению). Тогда общее число наблюдений 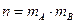. Обозначим через 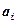математическое ожидание 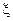при уровне 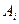, 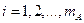; через 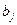— математическое ожидание 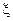при уровне 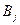, 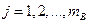. Если при изменении фактора 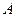сохраняется равенство 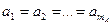, то естественно считать, что величина 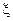не зависит от фактора 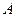, принимается нулевая гипотеза 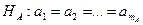. В противном случае, 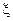зависит от фактора 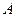. Аналогично определяется зависимость от фактора 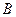, нулевая гипотеза .

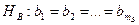При решении задачи будем предполагать, что выполняются следующие условия: наблюдения при различных сочетаниях уровней факторов независимы и при всех сочетаниях уровней факторов случайная величина 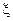нормально распределена с одной и той же дисперсией .
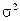Изменчивость наблюдаемых факторов при переходе от одной клетки таблицы к другой может быть обусловлена как изменением уровней факторов, так и случайными неконтролируемыми факторами.
Изменчивость, вызванная случайными неконтролируемыми факторами, называется остаточной.

Вычислим общую среднюю результатов измерений по формуле
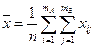. Эту величину можно представить в другой форме, использующей групповые средние 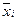и :

, .

Точка в индексе величины 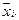означает, что суммирование ведется по i-й строке, а точка в индексе величины 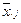означает, что суммирование ведется по j-му столбцу.
В этих обозначениях средняя результатов измерений вычисляется по формуле 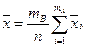или .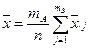

Средняя изменчивость, вызванная фактором 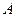, вычисляется по формуле
.

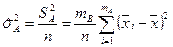Аналогично для изменчивости, вызванной фактором :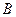
.
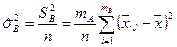Для характеристики изменчивости, обусловленной случайными факторами, вычисляем
.
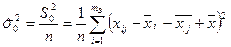Общую изменчивость величины 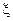характеризуют величиной
.
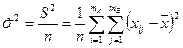Доказано, что .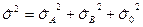

Проверка гипотезы 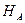основывается на сравнении величин 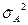и .
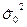Если гипотеза 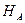верна, то величина 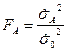имеет распределение Фишера со степенями свободы 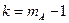и .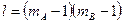
Зададимся уровнем значимости 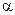и найдем правостороннюю критическую точку 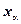— решение уравнения .

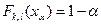Если значение 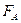, вычисленное по результатам измерений удовлетворяет неравенству 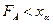, то гипотеза 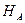принимается.
В противном случае – отвергается и можно заключить, что изменение фактора 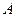влияет на изменение величины 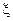. Мерой этого влияния является коэффициент детерминации 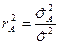, который показывает, какая доля общей изменчивости величины 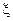обусловлена увеличением фактора .
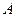Аналогично проверяется гипотеза 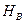основывается на сравнении величин 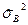и .

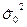Если гипотеза 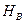верна, то величина 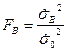имеет распределение Фишера со степенями свободы 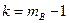и .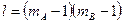
При уровне значимости 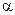правосторонняя критическая точка 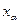— решение уравнения 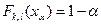. Если значение 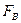, вычисленное по результатам измерений удовлетворяет неравенству ,
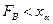то гипотеза 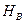принимается.
В противном случае гипотеза 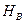отвергается и можно заключить, что изменение фактора 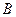влияет на изменение величины 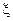. Мерой этого влияния является коэффициент детерминации 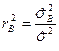, который показывает, какая доля общей изменчивости величины 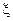обусловлена увеличением фактора .
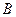В рамках двухфакторного дисперсионного анализа можно получить более конкретное представление о случайной величине .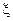
Ее модель на 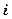-м уровне фактора A и на j-м уровне фактора B имеет вид
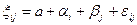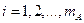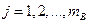, , , где a — генеральное среднее случайной величины 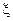, 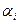— слагаемое, которое описывает эффект влияния фактора A на случайную величину 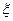на i-м уровне фактора A,
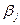— слагаемое, которое описывает эффект влияния фактора B на случайную величину 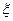на j-м уровне фактора B,
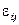— слагаемое, которое описывает эффект влияния случайных факторов.
Величины 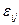— независимые случайные величины, имеющие одинаковое нормальное распределение .

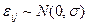Если гипотезы 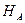и 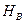не отвергаются, то в рассмотренной модели параметры

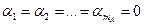и .

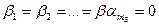Величина 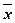является оценкой параметра 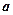, а величина 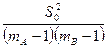— несмещенная оценка параметра .
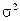Если гипотезы 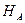и 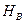отвергаются, то: оценка параметра a равна 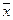, оценка параметр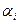а равна 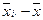, оценка параметр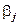а равна ,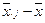
а величина 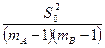служит несмещенной оценкой параметра .

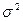Пример: Проведите двухфакторный дисперсионный анализ таблицы. Запишите уточнённую модель.

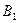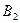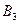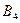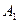	10.9	11.1	9.9	11.51
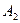	13.3	15.2	14.8	14.9
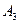	17.3	18.0	19.6	19.3

На приведенном ниже рисунке изображён фрагмент листа Excel c результатами вычислений.

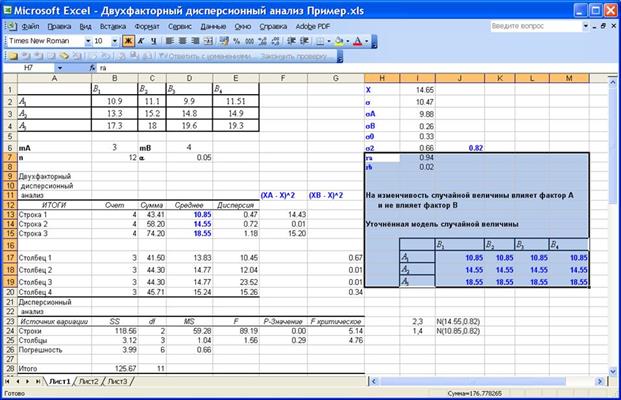
Выборочное значение критерия Фишера для фактора А попадает в критическую область, 89.19 > 5.14.
Фактор А является причиной изменчивости случайной величины.
Коэффициент детерминации для фактора Аравен rA=0.94. Это означает, что более 94% всей изменчивости исследуемой случайной величины обусловлено изменением фактора А. Выборочное значение критерия Фишера для фактора В не попадает в критическую область, 1.56 < 4.76.

Фактор В не является причиной изменчивости случайной величины.
На долю фактора Вприходится только 2% изменчивости, поскольку rВ=0.02.
Для всех уровней фактора случайные величины распределены нормально со стандартным отклонением 0.82 и математическими ожиданиями 10.852, 14.55 и 18.55 соответственно для каждого уровня фактора.
Матрица, описывающая влияние факторов на изучаемое явление – уточнённая матрица.

Так, например, на уровнях А2иВ3случайная величина имеет нормальное распределение

Дискриминантный анализ

Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы). Например, некий исследователь в области образования может захотеть исследовать, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающий в колледж, (2) поступающий в профессиональную школу или (3) отказывающийся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь может собрать данные о различных переменных, связанных с учащимися школы. После выпуска большинство учащихся естественно должно попасть в одну из названных категорий. Затем можно использовать Дискриминантный анализ для определения того, какие переменные дают наилучшее предсказание выбора учащимися дальнейшего пути.

Пошаговый дискриминантный анализ:

Вероятно, наиболее общим применением дискриминантного анализа является включение в исследование многих переменных с целью определения тех из них, которые наилучшим образом разделяют совокупности между собой.

Модель.Другими словами, вы хотите построить "модель", позволяющую лучше всего предсказать, к какой совокупности будет принадлежать тот или иной образец. В следующем рассуждении термин "в модели" будет использоваться для того, чтобы обозначать переменные, используемые в предсказании принадлежности к совокупности; о неиспользуемых для этого переменных будем говорить, что они "вне модели".

Пошаговый анализ с включением. В пошаговом анализе дискриминантных функций модель дискриминации строится по шагам. Точнее, на каждом шаге просматриваются все переменные и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу.

Пошаговый анализ с исключением.Можно также двигаться в обратном направлении, в этом случае все переменные будут сначала включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в предсказания. Тогда в качестве результата успешного анализа можно сохранить только "важные" переменные в модели, то есть те переменные, чей вклад в дискриминацию больше остальных.

F для включения, F для исключения. Эта пошаговая процедура "руководствуется" соответствующим значением F для включения и соответствующим значением F для исключения. Значение F статистики для переменной указывает на ее статистическую значимость при дискриминации между совокупностями, то есть, она является мерой вклада переменной в предсказание членства в совокупности. Если вы знакомы с пошаговой процедурой множественной регрессии, то вы можете интерпретировать значение F для включения/исключения в том же самом смысле, что и в пошаговой регрессии.

Расчет на случай.Пошаговый дискриминантный анализ основан на использовании статистического уровня значимости. Поэтому по своей природе пошаговые процедуры рассчитывают на случай, так как они "тщательно перебирают" переменные, которые должны быть включены в модель для получения максимальной дискриминации. При использовании пошагового метода исследователь должен осознавать, что используемый при этом уровень значимости не отражает истинного значения альфа, то есть, вероятности ошибочного отклонения гипотезы H₀ (нулевой гипотезы, заключающейся в том, что между совокупностями нет различия).

Интерпретация функции дискриминации для двух групп:

Для двух групп дискриминантный анализ может рассматриваться также как процедура множественной регрессии (и аналогичная ей) - (см. раздел Множественная регрессия; дискриминантный анализ для двух групп также называется Линейным дискриминантным анализом Фишера после работы Фишера (Fisher, 1936). (С вычислительной точки зрения все эти подходы аналогичны). Если вы кодируете две группы как 1 и 2, и затем используете эти переменные в качестве зависимых переменных в множественной регрессии, то получите результаты, аналогичные тем, которые получили бы с помощью Дискриминантного анализа. В общем, в случае двух совокупностей вы подгоняете линейное уравнение следующего типа:

Группа = a + b₁*x₁ + b₂*x₂ + ... + b_m*x_m

где a является константой, и b₁...b_m являются коэффициентами регрессии. Интерпретация результатов задачи с двумя совокупностями тесно следует логике применения множественной регрессии: переменные с наибольшими регрессионными коэффициентами вносят наибольший вклад в дискриминацию.

Дискриминантные функции для нескольких групп:

Если имеется более двух групп, то можно оценить более, чем одну дискриминантную функцию подобно тому, как это было сделано ранее. Например, когда имеются три совокупности, вы можете оценить: (1) - функцию для дискриминации между совокупностью 1 и совокупностями 2 и 3, взятыми вместе, и (2) - другую функцию для дискриминации между совокупностью 2 и совокупности 3. Например, вы можете иметь одну функцию, дискриминирующую между теми выпускниками средней школы, которые идут в колледж, против тех, кто этого не делает (но хочет получить работу или пойти в училище), и вторую функцию для дискриминации между теми выпускниками, которые хотят получить работу против тех, кто хочет пойти в училище. Коэффициенты b в этих дискриминирующих функциях могут быть проинтерпретированы тем же способом, что и ранее.