Б. Решение методом статистической линеаризации

При вероятностном расчете системы вместо случайных величин используются их статистические характеристики: математические ожидания, дисперсии и корреляционные моменты.

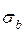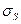Случайные прочности бетона и стали являются статистически независимыми величинами, тогда K_b,s=0. Математические ожидания m_b, m_s и стандарты и можно вычислить исходя из соответствующих нормативных значений.

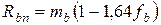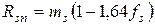; . (II.7)

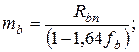
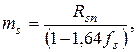
где, коэффициенты вариации бетона и стали AIII соответственно равны: f_b=0,135; f_s=0,0437;

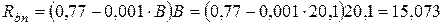МПа (значение В принимаем из примера 1).

Тогда:

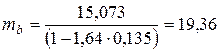МПа;

МПа;

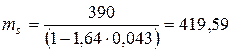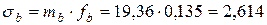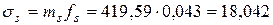МПа;

МПа.

Формула для вычисления предельного изгибающего момента в сечении как функции двух случайных величин 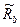и 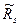, аналогична формуле метода предельных состояний, но целью вероятностного расчета является определение не одного из возможных значений случайной величины момента (расчетного значения М), а нахождение его статистических характеристик. Это дает возможность описать всю совокупность возможных значений предельного изгибающего момента.

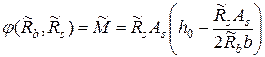. (II.8)

Математическое ожидание случайной величины 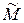находится по формуле (II.8) в которой вместо случайных параметров 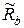и 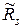поставлены их математические ожидания:

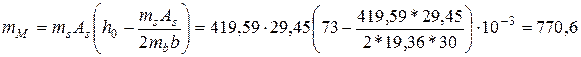кНм

Дисперсия изгибающего момента находится по формуле (II.6)

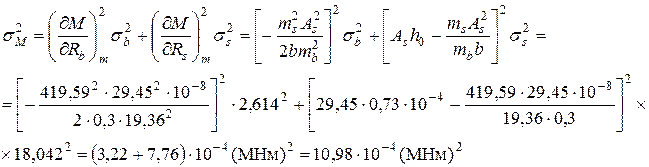
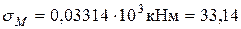кНм.