Множення матриць
Множення матриць розглянемо, починаючи з відомого вже прикладу 3, при підрахунку грошових затрат на виконання робіт по проходці в шахті (метро, тунелі). Нехай в рядках матриці
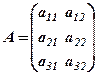
записані результати роботи за добу кожної із трьох змін: по виїмці породи (перший стовпець) і по кріпленню пройденої виробки (другий стовпець). Як вже згадувалось, при заданій площі поперечного перетину проходки результати робіт можуть вимірюватись в пройденних погонних метрах. Замовнику необхідно знати, яку суму грошей прийдеться виділяти на оплату праці робітників, а яку – на капітальні витрати. Існують норми розцінок на зарплату і капітальні витрати, які представимо у вигляді матриці розцінок
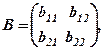
де перший стовпець 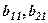 – норми оплати праці робітників: за 1 погонний метр по виїмці породи і за 1 погонний метр по кріпленню відповідно. Другий стовпець:
– норми оплати праці робітників: за 1 погонний метр по виїмці породи і за 1 погонний метр по кріпленню відповідно. Другий стовпець: 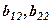 – відповідні капітальні затрати за 1 погонний метр виїмки і за 1 погонний метр кріплення.
– відповідні капітальні затрати за 1 погонний метр виїмки і за 1 погонний метр кріплення.
Загальні затрати на зарплату для кожної із змін дорівнюють сумі добутків пройдених кількостей метрів по обох видах робіт на відповідні норми розцінок. Позначимо через 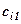 сумму грошей зароблену
сумму грошей зароблену 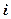 -ю зміною
-ю зміною 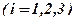 . Аналогічно підраховуються капітальні затрати
. Аналогічно підраховуються капітальні затрати 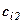 для
для 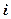 -ої зміни по виїмці і кріпленню.
-ої зміни по виїмці і кріпленню.
Отримаємо таблицю затрат
| Зміни | Затрати на зарплату по виїмці і кріпленню | Капітальні затрати по виїмці і кріпленню |
| І-а зміна | 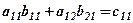 | 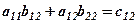 |
| ІІ-а зміна | 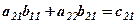 | 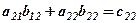 |
| ІІІ-я зміна | 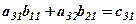 | 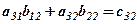 |
Ці дані запишемо у вигляді нової матриці затрат 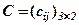 , що отримана з матриць
, що отримана з матриць 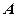 і
і 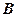 за допомогою операції, яку називають множенням матриць, і позначають
за допомогою операції, яку називають множенням матриць, і позначають
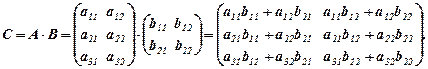
Для множення матриці 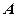 розміру
розміру 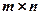 на матрицю
на матрицю 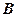 розміру
розміру 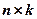 необхідна їх узгодженність, тобто, щоб число стовпців матриці
необхідна їх узгодженність, тобто, щоб число стовпців матриці 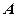 (першого співмножника) збігалося з числом рядків матриці
(першого співмножника) збігалося з числом рядків матриці 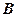 (другого співмножника). Так в наведеному прикладі матриця
(другого співмножника). Так в наведеному прикладі матриця 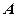 узгоджується з матрицею
узгоджується з матрицею 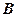 (для кожного виду робіт є норми розцінок). Однак матриця
(для кожного виду робіт є норми розцінок). Однак матриця 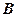 не є узгодженою з матрицею
не є узгодженою з матрицею 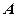 .
.
Означення 1. Добутком матриці 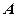 розміру
розміру 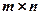 на матрицю
на матрицю 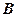 розміру
розміру 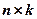 називається матриця
називається матриця 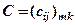 розміру
розміру 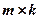 , елементи якої
, елементи якої 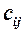 дорівнюють сумі добутків елементів
дорівнюють сумі добутків елементів 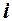 -того рядка матриці
-того рядка матриці 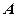 на відповідні елементи
на відповідні елементи 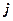 -того стовпця матриці
-того стовпця матриці 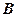 , тобто
, тобто
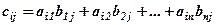 .
.
Із структури елементів 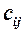 зрозуміло необхідність узгодженості матриць
зрозуміло необхідність узгодженості матриць 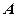 і
і 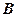 : кожному елементу в
: кожному елементу в 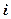 -тому рядку матриці
-тому рядку матриці 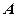 (першого співмножника) повинен відповідати елемент в
(першого співмножника) повинен відповідати елемент в 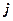 -тому стовпці матриці
-тому стовпці матриці 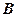 (другого співмножника). Число рядків матриці
(другого співмножника). Число рядків матриці 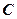 дорівнює числу рядків першого співмножника, а число стовпців- числу стовпців другого співмножника.
дорівнює числу рядків першого співмножника, а число стовпців- числу стовпців другого співмножника.
Приклад 1. Знайти добуток матриць 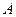 і
і 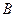 , якщо
, якщо 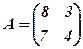 ,
, 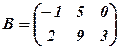 .
.
Розв’язання. Матриця 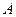 має розмір 2х2, розмір матриці
має розмір 2х2, розмір матриці 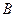 - 2х3. Число стовпців матриці
- 2х3. Число стовпців матриці 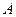 дорівнює 2 і збігається з числом рядків матриці
дорівнює 2 і збігається з числом рядків матриці 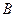 . Отже, матриці узгоджені, тому можна множити матрицю
. Отже, матриці узгоджені, тому можна множити матрицю 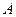 на матрицю
на матрицю 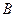 . В результаті отримаємо матрицю
. В результаті отримаємо матрицю 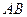 розміром 2х3, тобто
розміром 2х3, тобто
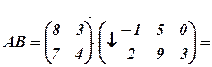
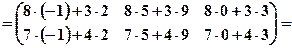
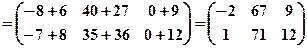 .
.
Приклад 2. Переконатись, що для даних матриць
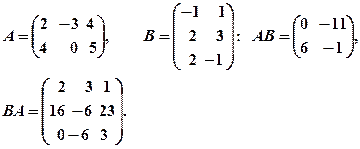
Звернути увагу, що в даному випадку 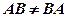 .
.
Приклад 3. Переконатись, що для даних матриць
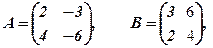
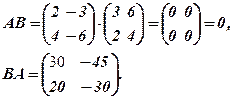
Звернути увагу, що добуток двох ненульових матриць може давати нульову матрицю, і, крім того, 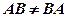 .
.
