Нахождение области определения и области значений функции

Раздел 1. Математический анализ

Тема 1.1. Функция. Предел функции

План

1. Числовые множества.

2. Функция одной переменной.

3. Простейшие элементарные функции

4. Построение графиков функций

5. Пределы, их свойства.

6. Нахождение пределов.

7. Задачи для самостоятельной работы.

Д/З: выучить лекцию, сделать ксерокопии таблиц(производной, дифференциалов, интегралов)

Числовые множества

Опр.Множество Х называется подмножеством множества У, если каждый элемент множества Х является элементом множества У.

Пример1.1Препараты, относящиеся к антидепрессантам, являются подмножеством психотропных средств.

Пример1.2

N

Z

I

Q

R

Натуральные числа – числа, которые используются для счёта предметов. N = {1, 2, 3, 4, …..}

Целые числа – натуральные числа и число 0. Z = {..., -3, -2, -1, 0, 1, 2, 3, 4, …}

Рациональные числа – числа, которые можно представить в виде 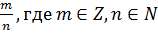. Q = N + Z +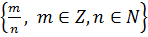

Иррациональные числа – числа, которые нельзя представить в виде 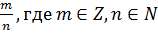. I = {π, ℓ, }

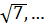Действительные числа – объединение рациональных и иррациональных чисел. R .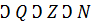

Функция одной переменной

Опр.Переменная величина уназывается функцией (или зависимой переменной) переменной величины х, называемой аргументом, или независимой переменной, если каждому допустимому значению х соответствует определённое значение у.

Множество значений, которое принимает переменная величина х, называют областью определения. Множество значений у, которое принимает функция, называют областью значений функции.

Способы задания функций:

1. Аналитический – правило соответствия задаётся в виде формулы.

2. Табличный– используется при проведении экспериментальных исследований. При этом данные заносятся в таблицу.

3. Графический– представляет запись изменения различных величин, например, от времени.

Словесный.

Нахождение области определения и области значений функции

При нахождении области определения функции, заданной аналитическим путём, независимая переменная принимает те значения, при которых функция существует. При этом следует учитывать, что:

1. Дробь имеет смысл, если знаменатель отличен от нуля;

2. Корень чётной степени существует, если подкоренное выражение не отрицательно;

3. Корень нечётной степени существует при любом значении подкоренного выражения;

4. Функция 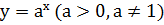определена на множестве всех действительных чисел, т. е. ;

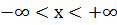5. Логарифмы отрицательных чисел не существуют;

6. Область определения функций 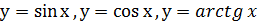является множество всех действительных чисел, т. е. ;

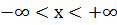7. Функция у = tg x определена, если ;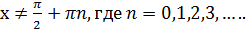

8. Функция у = arcsin x и y = arсcos x определены, если .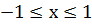

Для нахождения области значения функции необходимо подставлять значения аргумента в аналитическую формулу и определять границы, в которых находятся изменения зависимой переменной.

Пример 2.1 .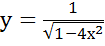

ОО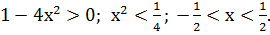Ф: ОЗФ: .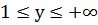

Обратная функция

Если для каждого значения у из множества значений функции у = f (x) становиться в соответствие одно или несколько значений х из области определения функции, то такая зависимость называется обратной функцией и обозначается х= У(у)

Чётные и нечётные функции

Опр.Функция у = f (x), определённая на промежутке, симметричном относительно начала координат, называется чётной, если для любого значения х из этой области определения f(-x) = f(x), и нечётной, если f(-x) = - f(x).

Периодические функции

Опр.Функция у = f (x) называется периодической, если существует такое положительное число Т, что f (x+Т)= f (x) для любого х из области определения функции.