Свободные затухающие колебания

ОБЩИЕ СВЕДЕНИЯ

Колебанияминазываются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Простейшим типом колебаний являются гармонические колебания– колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса.

Дифференциальное уравнение гармонических колебаний имеет вид

,

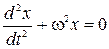где 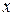- колеблющаяся величина, 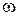- циклическая частота.

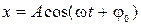- решение этого уравнения. Здесь 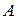- амплитуда, 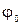- начальная фаза.

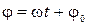- фаза колебаний.

Амплитуда – максимальное значение колеблющейся величины.

Период колебаний – промежуток времени, через который происходит повторение движения тела. Фаза колебания за период получает приращение 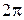. . 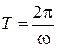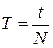, 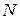- число колебаний.

Частота колебаний – число полных колебаний, совершаемых в единицу времени. 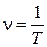. . 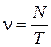Измеряется в герцах (Гц).

Циклическая частота – число колебаний, совершаемых за 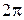секунд. 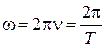. Единица измерения .

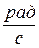Фаза колебаний – величина, стоящая под знаком косинуса и характеризующая состояние колебательной системы в любой момент времени.

Начальная фаза – фаза колебаний в начальный момент времени. Фаза и начальная фаза измеряются в радианах ( ).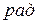

Свободные затухающие колебания– колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Дифференциальное уравнение свободных затухающих колебаний имеет вид

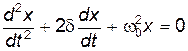, (1)

где x –	колеблющаяся величина, описывающая тот или иной физический процесс;
d –	коэффициент затухания;
w0 –	циклическая частота собственных незатухающих колебаний (собственная частота колебательной системы).

Решение уравнения (1) в случае малого затухания (d² << 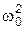) имеет вид

,

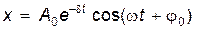где 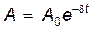–	амплитуда затухающих колебаний;
A0 –	начальная амплитуда;
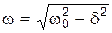–	циклическая частота затухающих колебаний;
j0 –	начальная фаза колебаний.

Промежуток времени 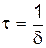, в течение которого амплитуда уменьшается в e раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими. Однако, если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя следующими друг за другом максимумами (или минимумами) колеблющейся величины. Тогда период затухающих колебаний вычисляют по формуле

.

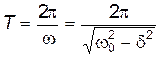Если A(t) и A(t+T)– амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

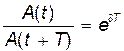
называется декрементом затухания, а его логарифм

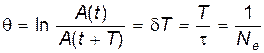– логарифмическим декрементом затухания.

Величина N_e – это число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная величина для данной колебательной системы.

Для характеристики колебательной системы используют понятие добротности Q, которая при малых значениях логарифмического декремента равна

.

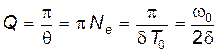Добротность пропорциональна числу колебаний, совершаемых системой за время релаксации.