В) если у этой точки существует такая окрестность, что в ней и слева и справа от точки знаки производной одинаковы, то в точке экстремума нет.

6.1) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
1) 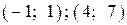
2) 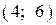
3) 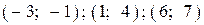
4) 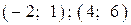
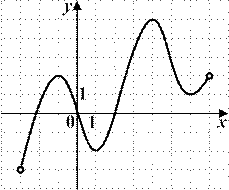
6.2) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, возрастает.
| 1) | 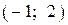 |
| 2) | 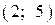 |
| 3) | 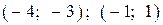 |
| 4) | 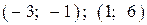 |
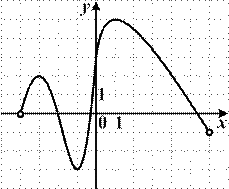
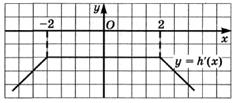
6.3) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
| 1) | 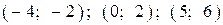 |
| 2) | 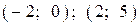 |
| 3) | 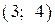 |
| 4) | 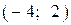 |
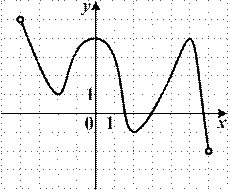
6.4) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
| 1) | 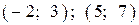 |
| 2) | 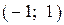 |
| 3) | 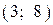 |
| 4) | 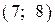 |
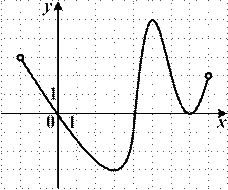
6.5) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
| 1) | 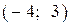 |
| 2) | 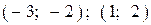 |
| 3) | 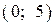 |
| 4) | 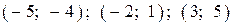 |
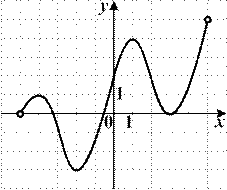
6.6) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, возрастает.
| 1) | 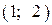 |
| 2) | 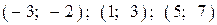 |
| 3) | 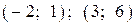 |
| 4) | 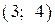 |
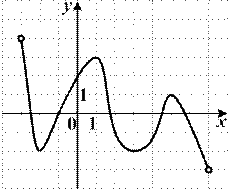
6.7) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
| 1) | 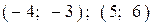 |
| 2) | 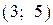 |
| 3) | 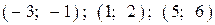 |
| 4) | 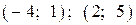 |
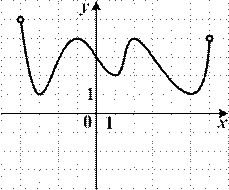
6.8) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, возрастает.
| 1) | 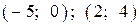 |
| 2) | 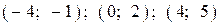 |
| 3) |  |
| 4) | 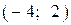 |
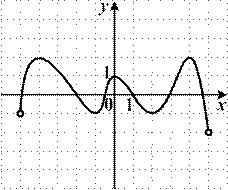
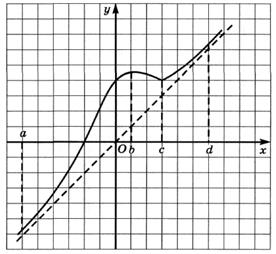
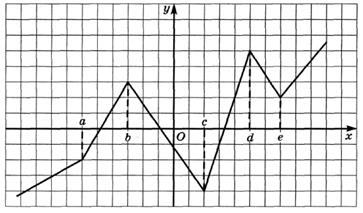
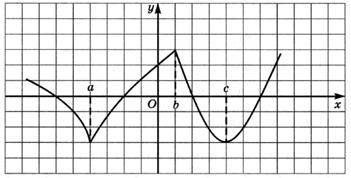
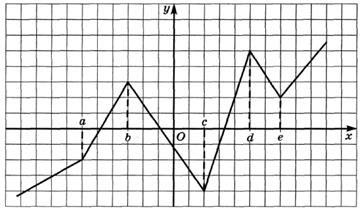
6.9) Определите, какой знак имеет производная функции 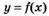 в точке с абсциссой а, если график функции изображен на рисунке:
в точке с абсциссой а, если график функции изображен на рисунке:
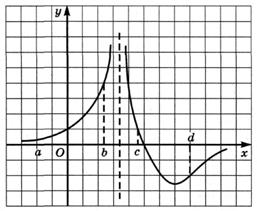
6.10) Определите, какой знак имеет производная функции  в точке с абсциссой b, если график функции изображен на рисунке:
в точке с абсциссой b, если график функции изображен на рисунке:

6.11) Определите, какой знак имеет производная функции 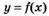 в точке с абсциссой с, если график функции изображен на рисунке:
в точке с абсциссой с, если график функции изображен на рисунке:
6.12) Определите, какой знак имеет производная функции 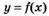 в точке с абсциссой d, если график функции изображен на рисунке:
в точке с абсциссой d, если график функции изображен на рисунке:

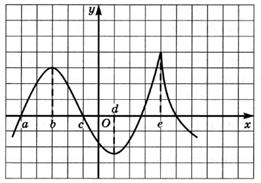
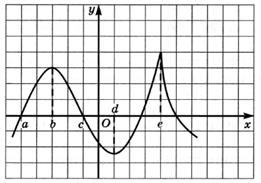
6.13) Определите, какой знак имеет производная функции 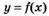 в точке с абсциссой а, если график функции изображен на рисунке:
в точке с абсциссой а, если график функции изображен на рисунке:
6.14) Определите, какой знак имеет производная функции 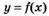 в точке с абсциссой b, если график функции изображен на рисунке:
в точке с абсциссой b, если график функции изображен на рисунке:
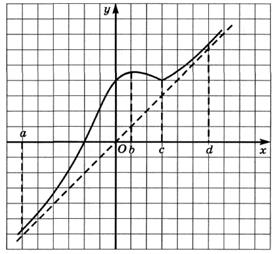
6.15) Определите, какой знак имеет производная функции  в точке с абсциссой с, если график функции изображен на рисунке:
в точке с абсциссой с, если график функции изображен на рисунке:

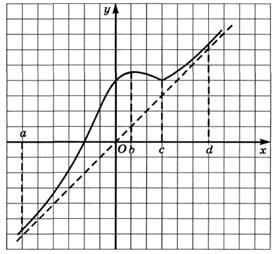
6.16) Определите, какой знак имеет производная функции  в точке с абсциссой d, если график функции изображен на рисунке:
в точке с абсциссой d, если график функции изображен на рисунке:
6.17) Определите промежуток (промежутки) возрастания функции, график которой изображен на рисунке:
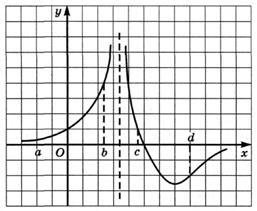
6.18) Определите промежуток (промежутки) убывания функции, график которой изображен на рисунке:
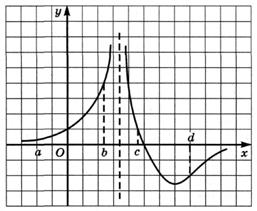
6.19) Определите промежуток (промежутки) возрастания функции, график которой изображен на рисунке:

6.20) Определите промежуток (промежутки) убывания функции, график которой изображен на рисунке:

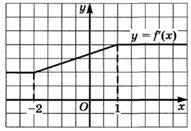
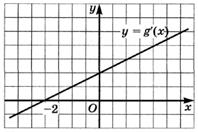
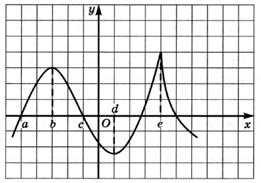
6.21) По графику производной, изображенному на рисунке,
определите, на каких промежутках функция  возрастает, а на каких — убывает:
возрастает, а на каких — убывает:
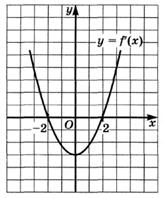
6.22) По графику производной, изображенному на рисунке,
определите, на каких промежутках функция 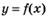 возрастает, а на каких — убывает:
возрастает, а на каких — убывает:
6.23) По графику производной, изображенному на рисунке,
определите, на каких промежутках функция 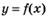 возрастает, а на каких — убывает:
возрастает, а на каких — убывает:
6.24) По графику производной, изображенному на рисунке,
определите, на каких промежутках функция 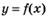 возрастает, а на каких — убывает:
возрастает, а на каких — убывает:
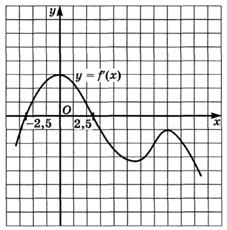
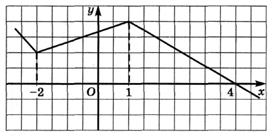
6.25) На каком из указанных промежутков функция 
убывает, если график ее производной представлен на
рисунке:
а) 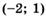 ; б)
; б) 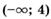 ; в)
; в) 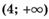 ; г)
; г) 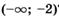 ?
?
6.26) Определите, для какой из функций, 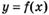 ,
, 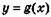
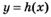 отрезок
отрезок 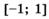 является промежутком возрастания, если на рисунках изображены графики производных этих функций.
является промежутком возрастания, если на рисунках изображены графики производных этих функций.
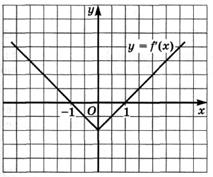
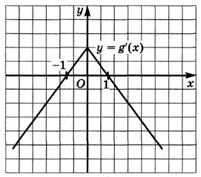
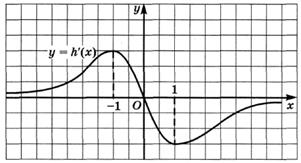
6.27) На рисунках изображены графики производных функций  ,
, 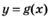 ,
, 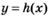 . Определите, какая из функций
. Определите, какая из функций 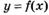 ,
, 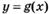 ,
, 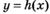 возрастает на R
возрастает на R
6.28) На рисунках изображены графики производных функций 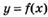 ,
, 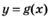 ,
, 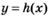 . Определите, какая из функций
. Определите, какая из функций 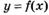 ,
, 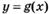 ,
, 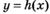 убывает на R
убывает на R
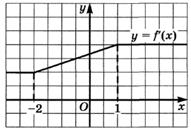
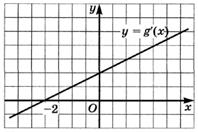
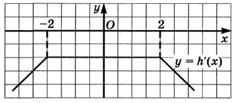
Определите промежутки монотонности функции:
6.29) 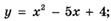
6.30) 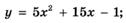
6.31) 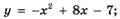
6.32) 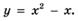
6.33) 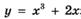 ;
;
6.34) 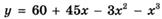 ;
;
6.35) 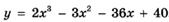 ;
;
6.36) 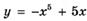
Исследуйте функцию на монотонность:
6.37) 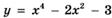 ;
;
6.38) 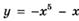 ;
;
6.39) 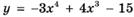 ;
;
6.40) 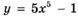
6.41) 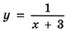 ;
;
6.42) 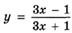 ;
;
6.43) 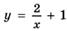 ;
;
6.44) 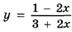
6.45) 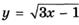 ;
;
6.46) 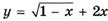 ;
;
6.47) 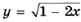 ;
;
6.48) 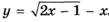
6.49) По графику функции 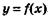 , изображенному на задан-
, изображенному на задан-
ном рисунке, определите точки, в которых ее производная обращается в 0:
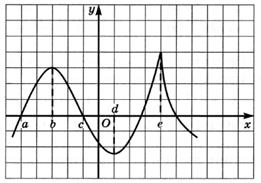
6.50) По графику функции 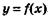 , изображенному на задан-
, изображенному на задан-
ном рисунке, определите точки, в которых ее производная обращается в 0:
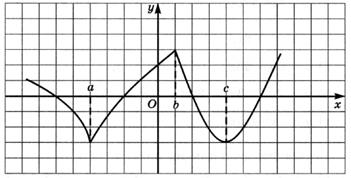
6.51) По графику функции 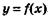 , изображенному на задан-
, изображенному на задан-
ном рисунке, определите точки, в которых ее производная обращается в 0:
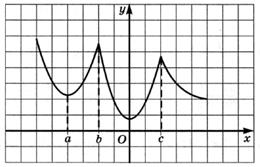
6.52) По графику функции 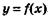 , изображенному на задан-
, изображенному на задан-
ном рисунке, определите точки, в которых ее производная обращается в 0:
6.53) По графику функции  , изображенному на рисунке, определите точки, в которых
, изображенному на рисунке, определите точки, в которых  не существует:
не существует:
6.54) По графику функции 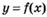 , изображенному на рисунке, определите точки, в которых
, изображенному на рисунке, определите точки, в которых 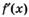 не существует:
не существует:
6.55) По графику функции 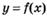 , изображенному на рисунке, определите точки, в которых
, изображенному на рисунке, определите точки, в которых 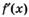 не существует:
не существует:
6.56) По графику функции 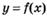 , изображенному на рисунке, определите точки, в которых
, изображенному на рисунке, определите точки, в которых  не существует:
не существует:

6.57) Сколько точек минимума имеет функция 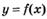 , график
, график
которой изображен на рисунке:
6.58) Сколько точек минимума имеет функция  , график
, график
которой изображен на рисунке:
6.59) Сколько точек минимума имеет функция 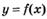 , график
, график
которой изображен на рисунке:
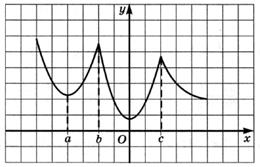
6.60) Сколько точек минимума имеет функция  , график
, график
которой изображен на рисунке:
6.61) Сколько точек максимума имеет функция 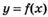 , график которой изображен на рисунке:
, график которой изображен на рисунке:
6.62) Сколько точек максимума имеет функция  , график которой изображен на рисунке:
, график которой изображен на рисунке:
6.63) Сколько точек максимума имеет функция 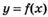 , график которой изображен на рисунке:
, график которой изображен на рисунке:

6.64) Сколько точек максимума имеет функция 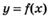 , график которой изображен на рисунке:
, график которой изображен на рисунке:
6.65) Используя данные о производной 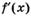 , приведенные
, приведенные
в таблице, укажите промежутки возрастания функции 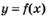

6.66) Используя данные о производной 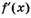 , приведенные в таблице, укажите промежутки убывания функции
, приведенные в таблице, укажите промежутки убывания функции 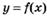 ;
;

6.67) Используя данные о производной 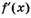 , приведенные в таблице, укажите точки максимума функции
, приведенные в таблице, укажите точки максимума функции 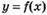 ;
; 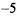

6.68) Используя данные о производной 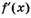 , приведенные в таблице, укажите точки минимума функции
, приведенные в таблице, укажите точки минимума функции 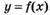

6.69) По графику производной, изображенному на рисунке, определите, имеет ли функция 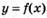 точки экстремума:
точки экстремума:
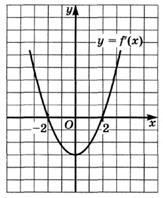
6.70) По графику производной, изображенному на рисунке, определите, имеет ли функция 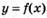 точки экстремума:
точки экстремума:

6.71) По графику производной, изображенному на рисунке, определите, имеет ли функция 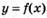 точки экстремума:
точки экстремума:
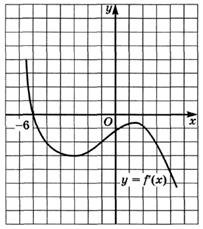
6.72) По графику производной, изображенному на рисунке, определите, имеет ли функция 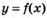 точки экстремума:
точки экстремума:
Найдите точки экстремума заданной функции и определите их характер:
6.73) 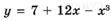 ;
;
6.74) 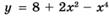 ;
;
6.75) 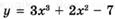 ;
;
6.76) 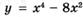
6.77) 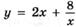 ;
;
6.78) 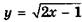 ;
;
6.79) 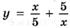 ;
;
6.80) 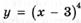
6.81) 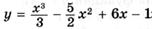 ;
;
6.82) 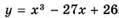
6.83) 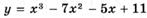
6.84) 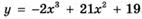
6.85)  ;
;
6.86)  ;
;
6.87) 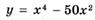 ;
;
6.88) 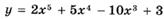
6.89) 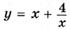 ;
;
6.90) 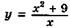 .
.
6.91) 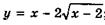 ;
;
6.92) 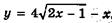
6.93) 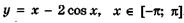 ;
;
6.94) 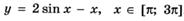
Ответы
 | |
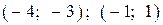 | |
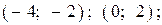 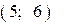 | |
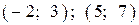 | |
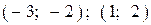 | |
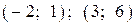 | |
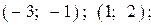 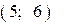 | |
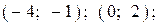 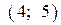 | |
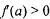 | |
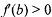 | |
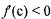 | |
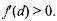 | |
| f(a) < 0 | |
| f(b) > 0 | |
| f(c) = 0 | |
| f(d) > 0 | |
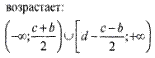 | |
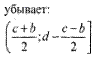 | |
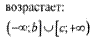 | |
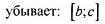 | |
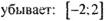 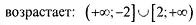 | |
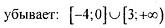 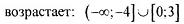 | |
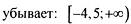 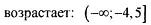 | |
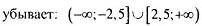 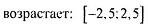 | |
| в) | |
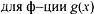 | |
 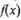 | |
 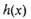 | |
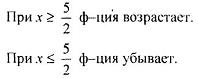 | |
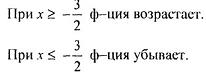 | |
 | |
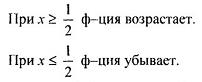 | |
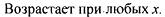 | |
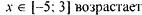 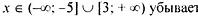 | |
 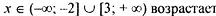 | |
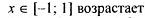 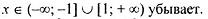 | |
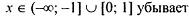 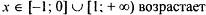 | |
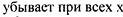 | |
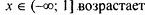 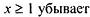 | |
 | |
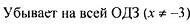 | |
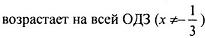 | |
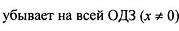 | |
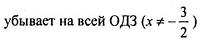 | |
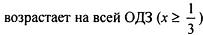 | |
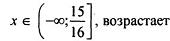 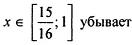 | |
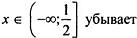 | |
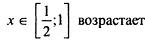 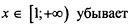 | |
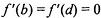 | |
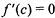 | |
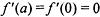 | |
 | |
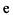 | |
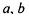 | |
 | |
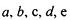 | |
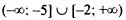 | |
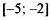 | |
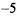 | |
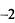 | |
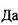 | |
 | |
 | |
 | |
| x = –2 точка минимума x = 2 точка максимума | |
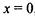 точка максимума точка максимума 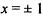 точки минимума точки минимума | |
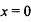 точка максимума точка максимума 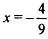 точка минимума точка минимума | |
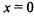 точка максимума точка максимума 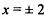 точки минимума точки минимума | |
| х = -2 — точка максимума, х = 2 — точка минимума | |
точек экстермума нет, функция возрастает на 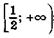 ; ; | |
| х = -5 — точка максимума, х = 5 — точка минимума | |
| х = 3 — точка минимума | |
| х = 2 — точка максимума, х = 3 — точка минимума | |
| х = -3 — точка максимума, х = 3 — точка минимума; в | |
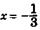 —точка максимума, х = 5 — точка минимума —точка максимума, х = 5 — точка минимума | |
| х = 7— точка максимума, х = 0— точка минимума | |
| х = 0,6 — точка максимума, х = -0,6 — точка минимума | |
| х = -1, х = 4 — точки минимума, х = 0 — точка максимума | |
| х = -5, х = 5 — точки минимума, х = 0 — точка максимума | |
| х = -3 — точка максимума, х = 1 — точка минимума. | |
| х = -2 — точка максимума, х - 2 — точка минимума | |
| х = -3 — точка максимума, х = 3 — точка минимума | |
| х = 3 — точка минимума | |
| х = 8,5 — точка максимума | |
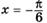 — точка минимума, — точка минимума, 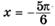 — точка максимума — точка максимума | |
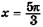 — точка минимума, — точка минимума, 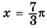 — точка максимума — точка максимума |
