Сызықтық теңдеулер жүйесін шешу тәсілдері.

№1

Матрица деп, m- жол және n- бағаннан тұратын сандар немесе әріптерден құрылған тік бұрышты кестені айтады.

Матрица латынның үлкен әріптерімен белгіленеді A,B,C,… және былай жазылады:

А матрицасын 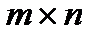өлшемді матрица дейді және оны 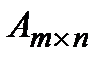деп жазады. Бір жолдан тұратын матрицаны жол-матрица дейді. Бір бағаннан тұратын матрицаны баған-матрица дейді. Егер матрицаның жолдарының саны бағандарының санына тең болса, ондай матрицаны квадрат матрицадейді. Оның өлшемі 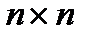болады.

Егер квадрат матрицаның бас диагональдан тыс элементтері нөлге тең болса, онда ондай матрицаны диагональ матрица дейді.

Егер диагональ матрицаның бас диагоналі бір сандарынан тұрса, онда ондай матрицаны бірлік матрица дейді және оны Е деп белгілейді.

Егер квадрат матрицаның бас диагоналінің бір жағына орналасқан элементтері түгелдей нөлге тең болса, онда оны үшбұрышты матрица дейді.

Егер матрицаның барлық элементтері нөлге тең болса, онда ондай матрицаны

нөлдік матрица дейді.

А матрицасының жолдарын сәйкес бағандар етіп алмастырғаннан пайда болған матрицаны транспонирленген матрица деп атайды және оны 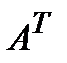деп белгілейді. Транспонирлеу амалының қасиеттері: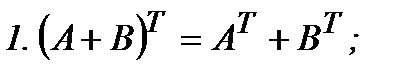

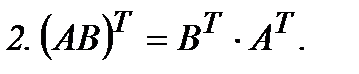
№2

Матрицаларға амалдар қолдану.Қосу амалы амалы өлшемдері бірдей матрицалар үшін ғана енгізіледі. Екі 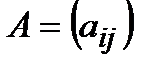және матрицаларының қосындысы деп, элементтері

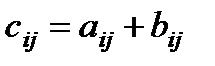болатын 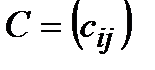матрицасын айтады және оны 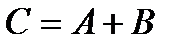деп белгілейді.. 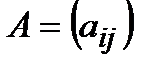матрицасын 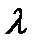санына көбейту деп әрбір элементі болатын матрицасын айтады.

Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері:

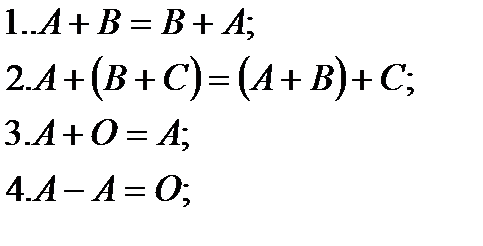
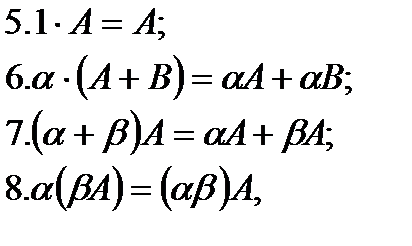
мұндағы 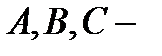матрицалар, 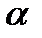және 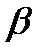- сандар.

Матрицаларды көбейту амалының қасиеттері:

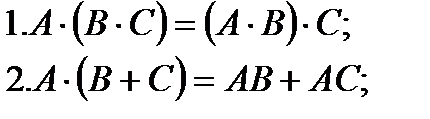
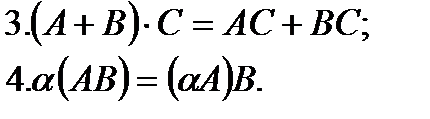
№3

Анықтауыштар.Анықтауыш сатылы түрде анықталады.

1) Кезкелген сан бірінші ретті анықтауыш.

2) Өлшемділігі 2-ге тең квадрат матрица 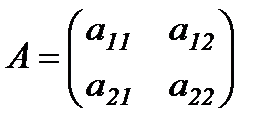үшін саны (мұндағы 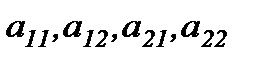- нақты сандар) А матрицасының анықтауышы немесе 2-ші ретті анықтауыш деп аталады және ол , 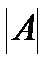, , 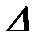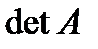деп белгіленеді.

А матрицасының анықтауышы немесе 3-ші ретті анықтауышы деп, төменгі формуламен есептелінетін санды айтады:

.

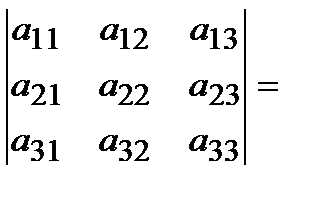
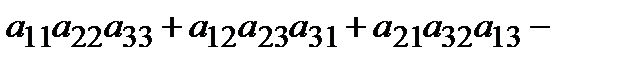
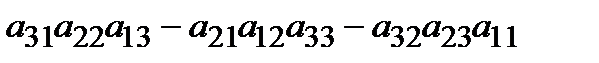№4

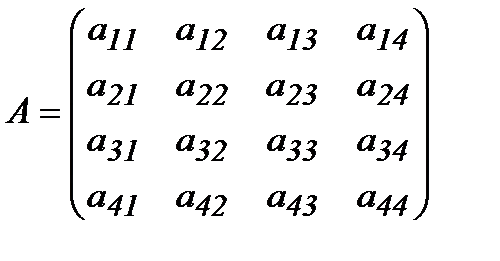квадрат матрицасының 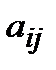элементінің миноры деп, осы элемент орналасқан жол мен бағанды сызып тастағаннан шығатын 3-ші ретті анықтауышты айтады және оны 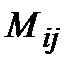деп белгілейді. Ал 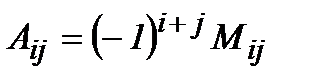саны 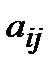элементінің алгебралық толықтауышы деп аталады.

№5

А матрицасының рангі деп осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады және оны 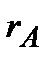, 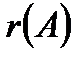немесе 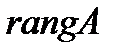деп белгілейді. 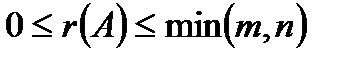болады, мұндағы 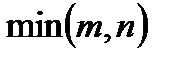- m және n сандарының кішісі. Матрицаны элементар түрлендіру деп:

1. матрицаның екі жолын (бағанын) ауыстыру;

2. матрицаның жолын (бағанын) нөлге тең емес санға көбейту;

3. бір жол (баған) элементтеріне басқа жолдың (бағанның) сәйкес қандай да бір санға көбейтілген элементтерін қосу амалдарын айтады.

Элементар түрлендіру арқылы алынған матрицаны бастапқы матрицаға эквивалентті матрица дейді және орталарына ~ белгісі қойылады. Матрицаның рангін табу үшін элементар түрлендіруді пайдаланып, матрицаны сатылы түрге келтіреміз.

Теорема. Матрицаны элементар түрлендіргеннен оның рангі өзгермейді.

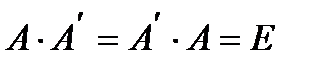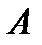Кері матрица.Егер шарты орындалса, онда матрицасын матрицасына кері матрица дейді және оны 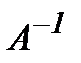түрінде белгілейді. Мұндағы 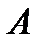, , 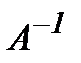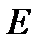матрицалары бірдей өлшемді квадрат матрицалар.

№6

Сызықтық алгебралық теңдеулер жүйесі.n белгісізі бар m теңдеулер жүйесі былай жазылады:

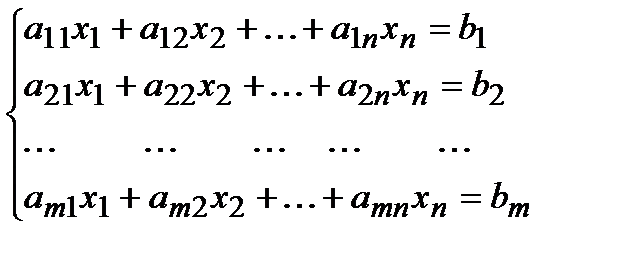
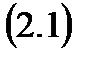
мұндағы 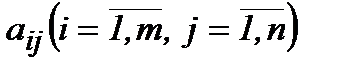жүйенің коэффициенттері, ал 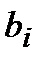- бос мүшелер деп аталады.

Егер теңдеулер жүйесінің кемінде бір шешімі бар болса, онда жүйе үйлесімді деп аталады, ал жүйенің бір де шешімі болмаса, онда жүйе үйлесімсіздеп аталады.

Егер А матрицасын бос мүшелерден тұратын бағанмен толықтырса, онда пайда болған матрицаны кеңейтілген матрица дейді және оны 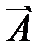деп белгілейді.

Сызықтық теңдеулер жүйесін шешу тәсілдері.

1. Крамер ережесі. Егер 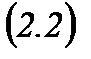жүйесі үшін 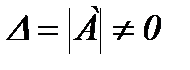болса, онда жүйенің жалғыз шешімі былайша табылады:

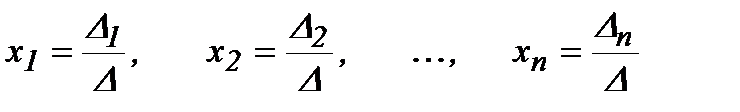
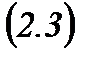
мұнда 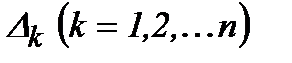- 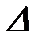анықтауышындағы 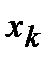белгісіздерінің коэффициеттерін бос мүшелермен алмастырғаннан пайда болған анықтауыш. 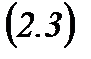Крамер формуласы деп аталады.

Матрицалық әдіс.n белгісізі бар n теңдеулер жүйесі, яғни 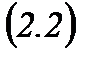жүйе берілсін. Жүйені матрицалық түрде былай жазамыз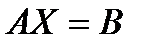

Теорема.Егер 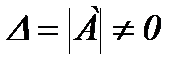болса, онда 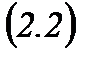жүйесінің 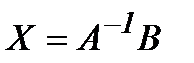теңдігімен анықталатын жалғыз шешімі бар.

3. Гаусс әдісі.n белгісізі бар m теңдеулер жүйесі, яғни 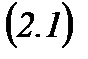берілсін. Жүйені Гаусс әдісімен шешу екі кезеңнен тұрады. Бірінші кезеңде (тік жүріс) жүйе трапеция тәріздес түрге келтіріледі.

№7

Вектор деп бағытталған кесіндіні айтады, яғни кесіндінің белгілі бір ұзындығы және бағыты болады. Егер А – вектордың басы, ал В –вектордың ұшы болса, онда вектор 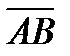немесе 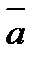символымен белгіленеді. 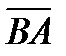векторы 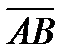векторына қарама-қарсы вектор деп атайды . ). 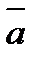векторына қарама-қарсы векторды 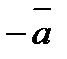деп белгілейді. 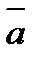векторының ұзындығынемесе модулідеп 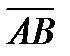кесіндісінің ұзындығын айтады және оны 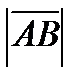немесе деп белгілейді. Ұзындығы нөлге тең векторды нөлдік вектор деп атайды және ол деп белгіленеді. Нөлдік вектордың бағыты болмайды.

Ұзындығы бірге тең векторды бірлік вектор деп атайды және оны 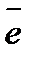деп белгілейді. Егер бірлік вектордың бағыты 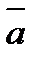векторының бағытымен сәйкес келсе, онда ол 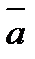векторының орты деп аталады және 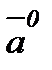деп белгіленеді.

Параллель түзулерде немесе бір түзудің бойында жататын векторлар коллинеар векторлар деп аталады және 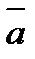|| 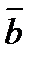деп белгіленеді. Коллинеар векторлар бағыттас болуы да, қарама-қарсы бағытта да болуы мүмкін.

Егер кеңістіктегі үш вектор бір жазықтықта немесе параллель жазықтықтарда жатса, онда олар компланар векторлар деп аталады.

№8