Электростатика и постоянный ток 3 страница

Работа А' внешней силы по перемещению заряда Qиз однойточки поля с потенциалом j₁ в другую, потенциал которой j₂, равна по модулю и противоположна по знаку работе А сил поля по перемещению заряда между теми же точками:

А'= – А.

Работа А сил поля по перемещению заряда A=Q(j₁ – j₂). Тогда работа А' внешних сил может быть записана в виде

A'= – Q(j₁ – j₂)=Q(j₂ – j₁). (1)

Потенциалы точек начала и конца пути выразятся формулами

; .

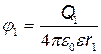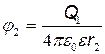Подставляя выражения j₁ и j₂ в формулу (1) и учитывая, что для данного случая переносимый заряд Q=Q₂, получим

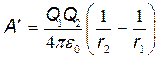. (2)

Если учесть, что 1/(4pe₀)=9×10⁹ м/Ф, то после подстановки значений величин в формулу (2) и вычисления найдем

A'=180 мкДж.

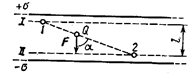Пример 12. Найти работу А поля по перемещению заряда Q=10 нКл из точки 1 в точку 2 (рис. 34), находящиеся между двумя разноименно заряженными с поверхностной плотностью s =0,4 мкКл/м² бесконечными параллельными плоскостями, расстояние l между которыми равно 3 см.

Решение. Возможны два способа решения задачи.

1-й способ. Работу сил поля по перемещению заряда Q из точки 1 поля с потенциалом j₁ в точку 2 поля с потенциалом j₂ найдем по формуле

A=Q(j₁ – j₂). (1)

Для определения потенциалов в точках 1 и 2 проведем через эти точки эквипотенциальные поверхности I и II. Эти поверхности будут плоскостями, так как поле между двумя равномерно заряженными бесконечными параллельными плоскостями однородно. Для такого поля справедливо соотношение

j₁ – j₂=El,(2)

где Е — напряженность поля; l — расстояние между эквипотенциальными поверхностями.

Напряженность поля между параллельными бесконечными разноименно заряженными плоскостями E=s/e₀. Подставив это выражение Е в формулу (2) и затем выражение j₁ – j₂ в формулу (1), получим

A=Q(s/e₀)l.

2-й способ. Так как поле однородно, то сила, действующая на заряд Q, при его перемещении постоянна. Поэтому работу перемещения заряда из точки 1 в точку 2 можно подсчитать по формуле

A=FDr cosa, (3)

где F — сила, действующая на заряд; Dr — модуль перемещения заряда Q из точки 1 в точку 2; a — угол между направлениями перемещения и силы. Но F=QE=Q(s /e₀). Подставив это выражение F в равенство (3), а также заметив, что Drcosa=l, получим

A=Q(s/e₀)l . (4)

Таким образом, оба решения приводят к одному и тому же результату.

Подставив в выражение (4) значение величин Q, s, e₀ и l, найдем

A=13,6 мкДж.

Пример 13. По тонкой нити, изогнутой по дуге окружности радиусом R, равномерно распределен заряд с линейной плотностью t =10 нКл/м. Определить напряженность 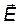и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке О, совпадающей с центром кривизны дуги. Длина l нити составляет 1/3 длины окружности и равна 15 см.

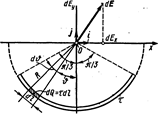
Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось у была симметрично расположена относительно концов дуги (рис. 35). На нити выделим элемент длины dl. Заряд dQ=tdl, находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность 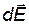поля, создаваемого зарядом dQ:

,

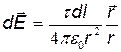где 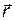— радиус-вектор, направленный от элемента dl к точке, напряженность в которой вычисляется. Выразим вектор 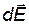через проекци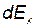и и 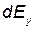на оси координат:

,

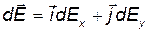где 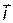и 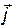— единичные векторы направлений (орты).

Напряженность 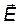найдем интегрированием:

.

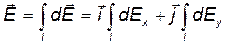Интегрирование ведется вдоль дуги длины l. В силу симметрии интеграл 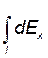равен нулю. Тогда

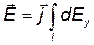, (1)

где 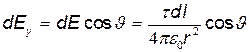. Так как r =R=const и dl=RdJ. то

.

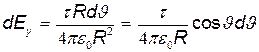Подставим найденное выражение 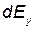в (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до p/3, а результат удвоим;

.

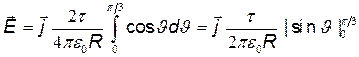Подставив указанные пределы и выразив R через длину дуги (3l=2p R), получим

.

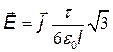Из этой формулы видно, что вектор 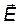совпадает с положительным направлением оси Оу Подставив значение t и l в последнюю формулу и сделав вычисления, найдем

E=2,18 кВ/м.

Определим потенциал электрического поля в точке О. Найдем сначала потенциал dj, создаваемый точечным зарядом dQ в точке О:

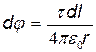
Заменим r на R и произведем интегрирование:

.

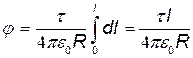Так как l=2pR/3, то

j =t/(6e₀).

Произведя вычисления по этой формуле, получим

j =188 В.

Пример 14. Электрическое поле создано длинным цилиндром радиусом R=1см, равномерно заряженным с линейной плотностью t=20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях a₁=0,5 см и а₂=2 см от поверхности цилиндра, в средней его части.

Решение. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала 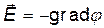. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

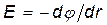, или dj = – Еdr.

Интегрируя последнее выражение, найдем разность потенциалов двух точек, отстоящих на r₁ и r₂ от оси цилиндра;

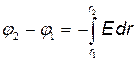. (1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой

.

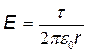Подставив это выражение Е в равенство (1), получим

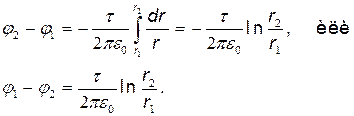(2)

Так как величины r₂ и r₁ входят в формулу в виде отношения, то их можно выразить в любых, но только одинаковых единицах:

r₁=R+a₁=1,5 см; r₂=R+a₂=3см.

Подставив значения величия t, e₀, r₁ и r₂ в формулу (2) и вычислив, найдем

j₁ – j₂=250 В.

Пример 15. Электрическое поле создано тонким стержнем, несущим равномерно распределенный по длине заряд t =0,1 мкКл/м. Определить потенциал j поля в точке, удаленной от концов стержня на расстояние, равное длине стержня.

Решение. Заряд, находящийся на стержне, нельзя считать точечным, поэтому непосредственно применить для вычисления потенциала формулу

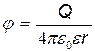, (1)

справедливую только для точечных зарядов, нельзя. Но если разбить стержень на элементарные отрезки dl, то заряд t·dl, находящийся на каждом из них, можно рассматривать как точечный и тогда формула (1) будет справедлива. Применив эту формулу, получим

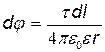, (2)

где r — расстояние точки, в которой определяется потенциал, до элемента стержня.

Из рис. 36 следует, что dl=(rda/cosa). Подставив это выражение dl в формулу (2), найдем .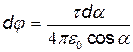

Интегрируя полученное выражение в пределах от a₁ да a₂, получим потенциал, создаваемый всем зарядом, распределенным на стержне:

.

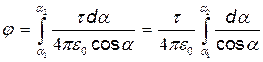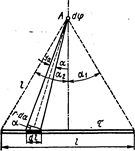В силу симметрии расположения точки А относительно концов стержня имеем a₂=a₁ и поэтому .

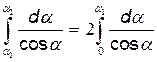Следовательно,

.

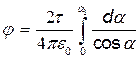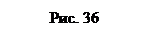Так как ,

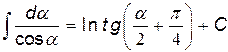то .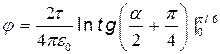

Подставляя пределы интегрирования, получим

Сделав вычисления по этой формуле, найдем

j =990 В.

Пример 16. Электрон со скоростью v =1,83×10⁶ м/с влетел в однородное электрическое поле в направлении, противоположном вектору напряженности поля. Какую разность потенциалов U должен пройти электрон, чтобы обладать энергией E_i =13,6 эВ? (Обладая такой энергией, электрон при столкновении с атомом водорода может ионизировать его.)

Решение. Электрон должен пройти такую разность потенциалов U, чтобы приобретенная при этом энергия W в сумме с кинетической энергией 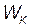, которой обладал электрон перед вхождением в поле, составила энергию, равную энергии ионизации E_i, т. е. W+ 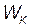=E_i. Выразив в этой формуле W=eU и 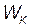=(mv²/2), получим eU+(mv²/2)=E_i. Отсюда

.

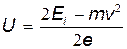Электрон-вольт (эВ) — энергия, которую приобретает частица, имеющая заряд, равный заряду электрона, прошедшая разность потенциалов 1 В. 1 эВ =1,6·10^-19 Дж.

Произведем вычисления в единицах СИ (масса электрона – 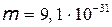кг; заряд электрона – 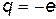, где 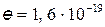Кл – элементарный заряд):

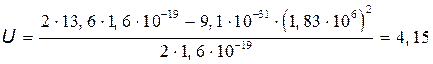В.

Пример 17.Определить начальную скорость 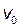сближения протонов, находящихся на достаточно большом расстоянии друг от друга, если минимальное расстояние r_min, на которое они могут сблизиться, равно 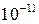см.

Решение. Между двумя протонами действуют силы отталкивания, вследствие чего движение протонов будет замедленным. Поэтому задачу можно решить как в инерциальной системе координат (связанной с центром масс двух протонов), так и в неинерциальной (связанной с одним из ускоренно движущихся протонов). Во втором случае законы Ньютона не имеют места. Применение же принципа Даламбера затруднительно из ‑ за того, что ускорение системы будет переменным. Поэтому удобно рассмотреть задачу в инерциальной системе отсчета.

Поместим начало координат в центр масс двух протонов. Поскольку мы имеем дело с одинаковыми частицами, то центр масс будет находиться в точке, делящей пополам отрезок, соединяющий частицы. Относительно центра масс частицы будут иметь в любой момент времени одинаковые по модулю скорости. Когда частицы находятся на достаточно большом расстоянии друг от друга, скорость 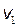каждой частицы равна половине 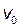, т. е. .

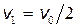Для решения задачи применим закон сохранения энергии, согласно которому полная механическая энергия 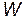изолированной системы постоянна, т. е.

,

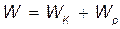где 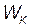- сумма кинетических энергий обоих протонов относительно центра масс; 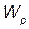- потенциальная энергия системы зарядов.

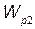Выразим потенциальную энергию в начальный и конечный моменты движения.

В начальный момент, согласно условию задачи, протоны находились на большом расстоянии, поэтому потенциальной энергией можно пренебречь ( =0). Следовательно, для начального момента полная энергия будет равна кинетической энергии 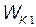протонов, т. е.

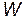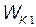= . (1)

В конечный момент, когда протоны максимально сблизятся, скорость и кинетическая энергия равны нулю, а полная энергия будет равна потенциальной энергии 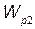, т. е.

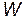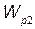= . (2)

Приравняв правые части равенств (1) и (2), получим

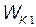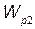= . (3)

Кинетическая энергия равна сумме кинетических энергий протонов:

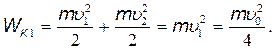(4)

Потенциальная энергия системы двух зарядов Q₁ и Q₂, находящихся в вакууме, определяется по формуле 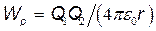, где r - расстояние между зарядами. Воспользовавшись этой формулой, получим

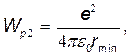(5)

С учетом равенств (4) и (5) формула (3) примет вид

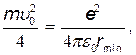откуда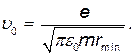

Выполнив вычисления по полученной формуле (масса протона равна 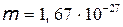кг), найдем 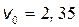Мм/с.

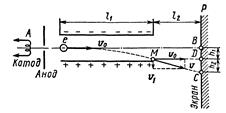
Пример 18. Электрон без начальной скорости прошел разность потенциалов U₀=10кВ и влетел в пространство между пластинами плоского конденсатора, заряженного до разности потенциалов U_l=100 В, по линии АВ, параллельной пластинам (рис. 37). Расстояние d между пластинами равно 2 см. Длина l₁ пластин конденсатора в направлении полета электрона, равна 20 cм. Определить расстояние ВС на экране Р,отстоящем от конденсатора на l₂=1 м.

Решение. Движение электрона внутри конденсатора складывается из двух движений: 1) по инерции вдоль линии АВ с постоянной скоростью 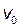,приобретенной под действием разности потенциалов U₀,которую электрон прошел до конденсатора; 2) равномерно ускоренного движения в вертикальном направлении к положительно заряженной пластине под действием постоянной силы поля конденсатора. По выходе из конденсатора электрон будет двигаться равномерно со скоростью 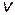,которую он имел в точке М в момент вылета из конденсатора.

Из рис. 37 видно, что искомое расстояние |BC|=h₁+h₂, где с h₁ - расстояние, на которое сместится электрон в вертикальном направлении во время движения в конденсаторе; h₂- расстояние между точкой D на эк­ране, в которую электрон попал бы, двигаясь по выходе из конденсатора по направлению начальной скорости υ₀, и точкой С, в которую электрон попадет в действительности.

Выразим отдельно h₁ и h₂. Пользуясь формулой длины пути равномерно ускоренного движения, найдем

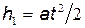. (1)

где а - ускорение, полученное электроном под действием поля конденсатора; t - время полета электрона внутри конденсатора.

По второму закону Ньютона a=F/m,где F - сила, с которой поле действует на электрон; т - его масса. В свою очередь, F =eE=eU₁/d, где е – модуль заряда электрона; U₁ - разность потенциалов между пластинами конденсатора; d - расстояние между ними. Время полета электрона внутри конденсатора найдем из формулы пути равномерного движения 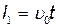, откуда

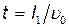
где l₁- длина конденсатора в направлении полета электрона. Выражение скорости найдем из условия равенства работы, совершенной полем при перемещении электрона, и приобретенной им кинетической энергии: 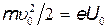. Отсюда

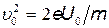(2)

Подставляя в формулу (1) последовательно значения а, F, t и 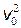из соответствующих выражений, получим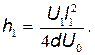

Длину отрезка h₂найдем из подобия треугольников MDC и векторного:

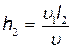, (3)

где 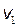- скорость электрона в вертикальном направлении в точке М; l₂ - расстояние от конденсатора до экрана.

Скорость 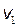найдем по формуле 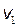=at,которая с учетом выражений для а, F и t примет вид

.

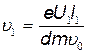Подставив выражение 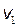в формулу (3), получим 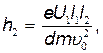или, заменив 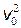по формуле (3), найдем

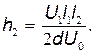
Окончательно для искомого расстояния |BC| будем иметь

|BC|=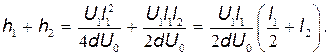

Подставив значения величин U₁, U₀, d, l₁ и l₂ в последнее выражение и произведя вычисления, получим |BC|=5,5cм.

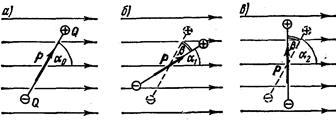Пример 19.Диполь с электрическим моментом р=2нКл·м находится в однородном электрическом поленапряженностью Е=30кВ/м. Вектор 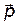составляет угол 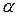=60˚ с направлением силовых линий поля. Опреде­лить произведенную внешними силами работу А поворота диполя на угол β=30°.

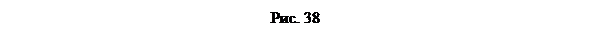Решение. Из исходного положения (рис. 38, а)диполь можно повернуть на угол β=30º=π/6двумя способами: или по часовой стрелке до угла α₁ =α₀ – β=π/3 – π/6=π/6(рис. 38, б), или против часовой стрелки до угла α₂=α₀+ β=π/3+π/6=π/2 (рис. 38, в).

В первом случае диполь будет поворачиваться под действием сил поля. Следовательно, работа внешних сил при этом отрицательна. Во втором случае поворот может быть произведен только под действием внешних сил, и, следовательно, работа внешних сил при этом положительна.

Работу, совершаемую при повороте диполя, можно вычислять двумя способами: 1) непосредственно интегрированием выражения элементарной работы; 2) с помощью соотношения между работой и изменением потенциальной энергии диполя в электрическом поле.

1-й способ. Элементарная работа при повороте диполя на угол α

dA=Md 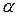=pE sin 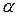d ,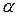

а полная работа при повороте на угол от 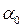до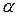

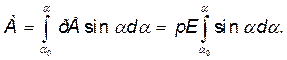
Произведя интегрирование, получим

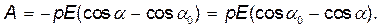(1)

Работа внешних сил при повороте диполя по часовой стрелке

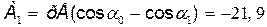мкДж,

против часовой стрелки

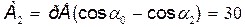мкДж.

2-й способ. Работа А внешних сил связана с изменением потен­циальной энергии Δ 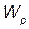соотношением A=Δ 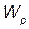= 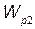– , где и 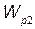– потенциальные энергии системы соответственно в начальном и конечном состояниях. Так как потенциальная энергия диполя в электрическом поле выражается формулой 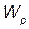= – рЕ cos 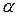,то

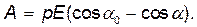(2)

что совпадает с формулой (1), полученной первым способом.

Пример 20. Определить электрическую емкость С плоского конденсатора с двумя слоями диэлектриков: фарфора толщиной d₁=2 мм и эбонита толщиной d₂= 1,5 мм, если площадь S пластин равна 100 см².

Решение. Емкость конденсатора, по определению, C=Q/U , где Q - заряд на пластинах конденсатора; U - разность потенциалов пластин. Заменив в этом равенстве общую разность потенциалов U конденсатора суммой U₁+U₂напряжений на слоях диэлектриков, получим

C=Q/(U₁+U₂). (1)