Пространственно-временные интервалы
При обычных вращениях системы координат инвариантом является квадрат расстояния между точками. Если одну точку для простоты поместить в начало координат, то квадрат расстояния между началом координат и точкой (х, у, z): х2+у2+z2, не меняется при поворотах.
Не трудно показать, что в случае пространства-времени есть комбинация квадратов координат, которая инвариантна по отношению ко всем инерциальным системам отсчета:
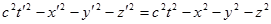
Поэтому эта величина, подобно расстоянию, носит название интервала между двумя пространственно-временными точками, одна из которых в этом случае совпадает с началом координат (точнее говоря, это квадрат интервала).
Если два события произошли в какой-то системе координат в одно и то же время, но в разных точках пространства, то, поместив начало координат в точку, изображающую одно из событий, мы получим, t = 0, а, например, х ¹ 0. Значит, квадрат интервала получится отрицательным, а сам интервал - мнимым. Интервалы бывают и действительные, и мнимые, потому что их квадраты могут быть и положительными, и отрицательными. Когда интервал мнимый, говорят, что интервал между событиями (точками) пространственно-подобный, потому что такой интервал получался бы всегда, если бы весь мир застыл на одном времени. С другой стороны, если два предмета в данной системе координат попадают в одно и то же место в разные моменты времени, тогда t ¹ 0, а х = у = z = 0 и квадрат интервала положителен; это называется времени-подобным интервалом. Далее, если провести на диаграмме пространства-времени (рисунок) две прямые под углом 450 (в четырех измерениях они обратятся в «конус», называемый световым, то точки на этих прямых будут отделены от начала координат нулевым интервалом. Куда бы из начала координат ни распространялся свет, все равно x2 + y2+ z2 = c2t2, т.е. интервал между событием прихода света в любую точку и началом координат всегда равен нулю. Это кстати говорит о инвариантности скорости света. Интервал будучи равен нулю в одной системе координат равен нулю и в любой другой системе координат, и квадрат скорости света - отношение  к
к 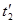 - опять равен с2.
- опять равен с2.
