Кинематика поступательного движения материальной точки и твердого тела
Д.т.н., проф. Селиванов Н.В., к.т.н., доц. Неупокоева И. В.
Рецензент: к. ф.-м. н., доц. Карибьянц В.Р.
Учебное пособие рассмотрено и утверждено к печати на заседании кафедры физики АГТУ (протокол № 10 от 16.09.2010)
Учебное пособие составлено на основании краткой теории, примеров решения задач, вопросов для самоподготовки и задач для самостоятельного решения по разделам курса общей физики: «Механика», «Молекулярная физика и термодинамика» для студентов инженерно-технических специальностей высшего учебного заведения.
СОДЕРЖАНИЕ СТР.
1. Кинематика поступательного движения
материальной точки и твердого тела…………………………………..4
2. Кинематика вращательного движения
материальной точки и твердого тела………………………………….23
3. Динамика поступательного движения
материальной точки и твердого тела………………………………….33
4. Динамика вращательного движения
материальной точки и твердого тела………………………………….52
5. Работа. Энергия. Законы сохранения…………………………………68
6. Молекулярная физика..………………………………………………....81
7. Теплоемкость. Первое начало термодинамики……………………….94
8. Второе начало термодинамики. Круговые процессы.
Цикл Карно. Энтропия……………………………………………….107
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА
Элементы векторной алгебры
Вектор – направленный отрезок или упорядоченная пара точек (например,  или
или 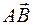 ). Про эти точки известно, какая из них первая (начало), а какая вторая (конец). Расстояние между началом и концом вектора называют его длиной(а также модулем и абсолютной величиной). Длина вектора
). Про эти точки известно, какая из них первая (начало), а какая вторая (конец). Расстояние между началом и концом вектора называют его длиной(а также модулем и абсолютной величиной). Длина вектора  обозначается
обозначается 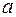 , вектора
, вектора 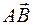 обозначается AB и находится по следующим формулам:
обозначается AB и находится по следующим формулам:
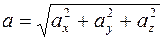 , (1.1)
, (1.1)
где 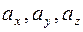 - проекции вектора
- проекции вектора  на оси декартовой системы координат x,y,z.
на оси декартовой системы координат x,y,z.
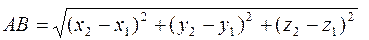 , (1.2)
, (1.2)
где 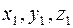 - координаты точки А,
- координаты точки А, 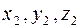 - координаты точки В.
- координаты точки В.
Сложение векторов(правило треугольника).Пусть даны два вектора  и
и 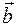 . Для сложения этих векторов перенесем параллельным переносом эти вектора в произвольную точку так, чтобы конец вектора
. Для сложения этих векторов перенесем параллельным переносом эти вектора в произвольную точку так, чтобы конец вектора  и начало вектора
и начало вектора 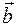 совпадали (рис.1.1). Тогда вектор
совпадали (рис.1.1). Тогда вектор 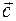 , соединяющий начало вектора
, соединяющий начало вектора  и конец вектора
и конец вектора 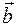 , называется суммой векторов
, называется суммой векторов  и
и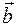 (
( 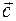 =
= 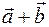 ).
).
Вычитание векторов.При вычитании векторов  и
и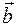 , необходимо перенести эти вектора параллельным переносом в произвольную точку, совмещая их начала (рис.1.2). Тогда вектор
, необходимо перенести эти вектора параллельным переносом в произвольную точку, совмещая их начала (рис.1.2). Тогда вектор 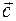 , соединяющий концы векторов
, соединяющий концы векторов  и
и 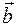 , и направленный к вектору
, и направленный к вектору  , из которого вычитали, называется разностью векторов
, из которого вычитали, называется разностью векторов  и
и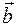 (
( 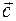 =
= 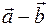 ).
).
|
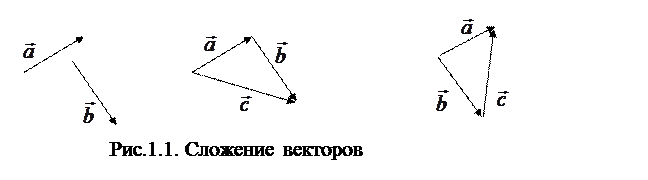
Произведением вектора  на вещественное число
на вещественное число 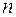 называется вектор
называется вектор 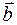 =
= 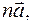 модуль которого в
модуль которого в 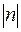 раз больше, чем модуль вектора
раз больше, чем модуль вектора 
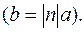 Направление же вектора
Направление же вектора 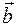 либо совпадает с направлением вектора
либо совпадает с направлением вектора  (если
(если 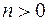 ), либо противоположно направлению вектора
), либо противоположно направлению вектора  (если
(если 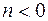 ).
).
Два вектора  и
и 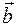 можно умножить друг на друга двумя способами; один способ приводит к скалярной величине, другой дает в результате некоторый новый вектор. В соответствии с этим существует два произведения векторов - скалярное и векторное.
можно умножить друг на друга двумя способами; один способ приводит к скалярной величине, другой дает в результате некоторый новый вектор. В соответствии с этим существует два произведения векторов - скалярное и векторное.
 Скалярным произведениемдвух векторов
Скалярным произведениемдвух векторов  и
и 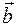 называется число с, равное произведению длин этих векторов на косинус угла между ними:
называется число с, равное произведению длин этих векторов на косинус угла между ними:
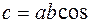
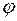 , (1.3)
, (1.3)
где 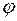 - угол между векторами
- угол между векторами  и
и 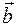 . Скалярное произведение векторов
. Скалярное произведение векторов 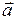 и
и 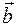 обозначается (
обозначается ( 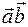 ) или
) или 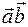 .
.
Векторным произведением двух векторов  и
и 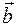 называется вектор
называется вектор 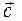 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 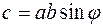 , (1.4)
, (1.4)
где 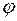 - угол между векторами
- угол между векторами  и
и 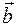 , sin
, sin 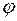
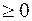 , так как 0
, так как 0 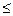
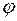
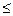 p;
p;
2) вектор 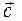 перпендикулярен плоскости, где лежат вектора
перпендикулярен плоскости, где лежат вектора  и
и 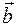 ;
;
3)направление 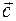 выбирается так, чтобы последовательность векторов
выбирается так, чтобы последовательность векторов 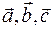 образовывала правовинтовую систему. Это означает, что, если смотреть вслед вектору
образовывала правовинтовую систему. Это означает, что, если смотреть вслед вектору 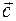 , то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке. (На рисунке 1.3 вектор
, то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке. (На рисунке 1.3 вектор 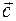 направлен за чертеж и поэтому изображен кружком с крестиком). Векторное произведение векторов
направлен за чертеж и поэтому изображен кружком с крестиком). Векторное произведение векторов  и
и 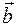 обозначается
обозначается 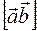 или
или 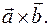

Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам
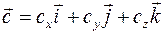 , (1.5)
, (1.5)
где 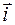 - единичный вектор оси ОХ,
- единичный вектор оси ОХ, 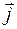 - оси ОY,
- оси ОY, 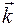 - оси OZ; сx, cy, cz – компоненты (или координаты) вектора
- оси OZ; сx, cy, cz – компоненты (или координаты) вектора 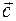 .
.
При умножении вектора 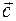 на вещественное число
на вещественное число 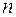 все его компоненты умножаются на это число:
все его компоненты умножаются на это число:
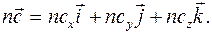 (1.6)
(1.6)
При сложении векторов складываются их соответствующие компоненты. Если 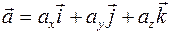 и
и 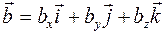 , то
, то
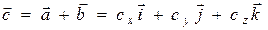 , где (1.7)
, где (1.7)
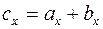 ,
, 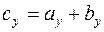 ,
, 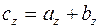 .
.
Скалярное произведение векторов 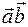 , представленных в виде (1.5), можно выразить через проекции перемножаемых векторов:
, представленных в виде (1.5), можно выразить через проекции перемножаемых векторов:
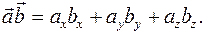 (1.8)
(1.8)
