Линейные дифференциальные уравнения первого порядка, структура общего решения линейного дифференциального уравнения, метод вариации произвольного постоянного

Опр. Линейным дифференциальным уравнением n-го порядканазывается уравнение, в которое неизвестная функция y(x)и её производные входят линейно, т.е. в первой степени:

Структура общего решения линейного дифференциального уравнения

Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения:
y(x) = C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x).

Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения частного решения.

16) Линейное дифференциальное уравнение энтого порядка

Линейным дифференциальным уравнением n-го порядканазывается уравнение, в которое неизвестная функция y(x)и её производные входят линейно, т.е. в первой степени:

17) Теорема о существовании единственности решения задачи Коши для линейного дифференциального уравнения энтого порядка

Теорема существования и единственности решения задачи Коши для линейного уравнения: если функции f(x), p_i(x), i = 1, 2, …, n непрерывны на интервале (a, b), x₀ - произвольная точка этого интервала, то для любых начальных условий

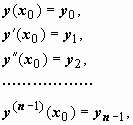существует единственная функция y(x), определённая на всём интервале (a, b) и удовлетворяющая уравнению ;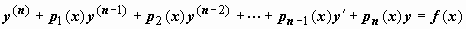

и начальным условиям

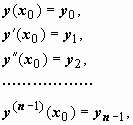18) Линейная зависимость и линейная независимость системы функции

Функции y₁(x), y₂(x), ..., y_n(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b] , если существуют постоянные α₁, α₂, ..., α_n , не равные нулю одновременно и такие, что α₁y₁(x) + α₂y₂(x) + ... + α_ny_n(x) = 0 для всех x из отрезка [a;b].

В противном случае функции y₁(x), y₂(x), ..., y_n(x) называются линейно независимыми.

Линейную зависимость и линейную независимость функций определяют также на (a;b) , (a;b] , [a;b) , на бесконечных промежутках.