Розв’язання. Спочатку складемо рівняння прямої , яка проходить перпендикулярно заданій площині через точку (Рис.35.1)

Зобразимо рисунок.

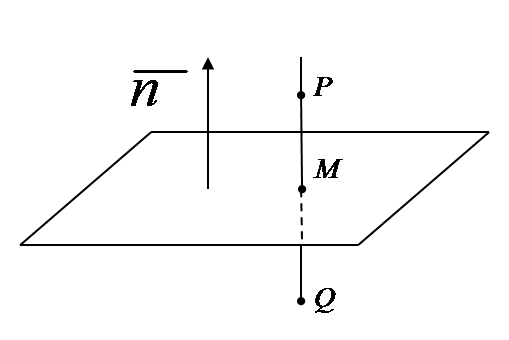
Рис.35.1

Спочатку складемо рівняння прямої 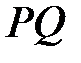, яка проходить перпендикулярно заданій площині через точку 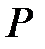(Рис.35.1). Нормальний вектор площини 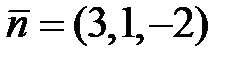буде одночасно напрямним вектором прямої, тому її рівнянням є

.

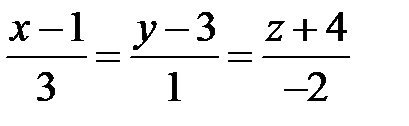Тепер знайдемо точку 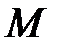– проекцію точки 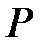на площину. Це точка перетину прямої та площини. Запишемо параметричне рівняння прямої.

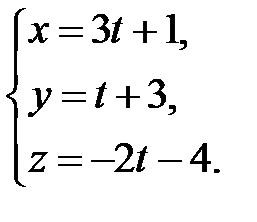
Підставимо одержані вирази в рівняння площини, щоб знайти значення параметра 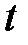, яке відповідає точці перетину прямої та площини.

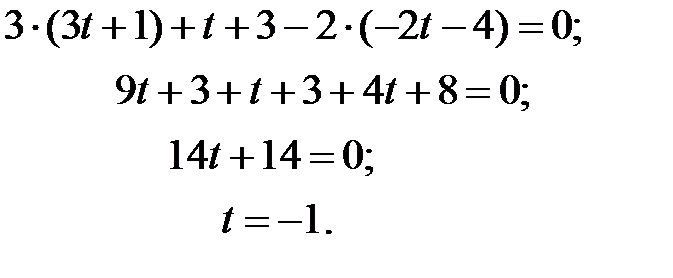
Знайдемо координати точки М.

.

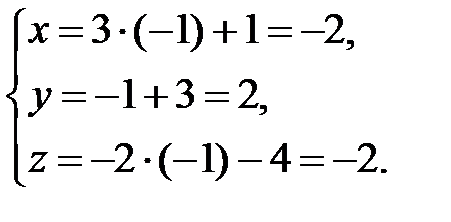
Отже,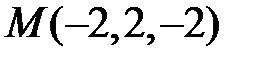

Для знаходження координат точки 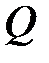скористаємось формулами координат середини відрізку (точка М є серединою ).

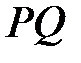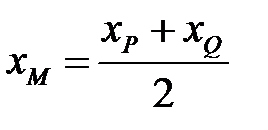, тоді .

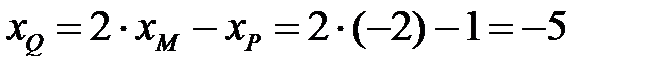Аналогічно

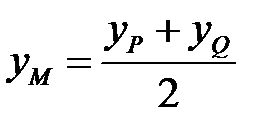, тоді ;

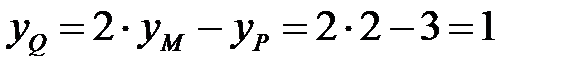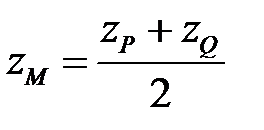, тоді .

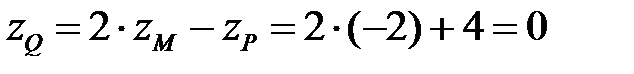Значить, симетрична точка має координати .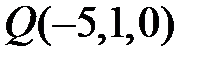

Задачі для самостійної роботи

1. Скласти рівняння прямої, що проходить через точку 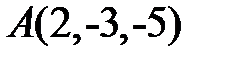перпендикулярно до площини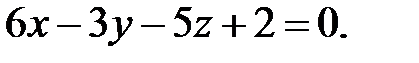

2. Скласти рівняння площини, яка проходить через точку 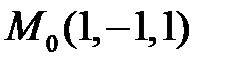перпендикулярно прямій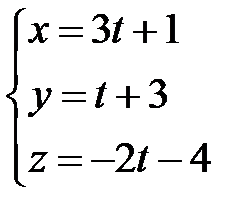

3. Знайти кут між прямою та площиною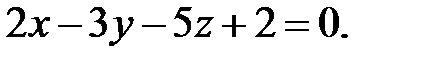

4. Знайти точку перетину прямої 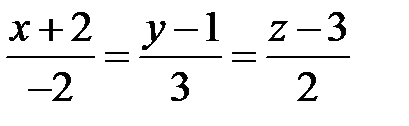та площини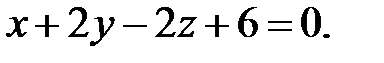

5. Скласти рівняння площини, яка проходить через пряму 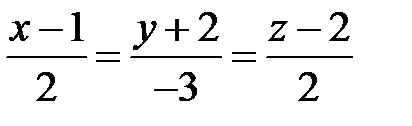перпендикулярно площині .

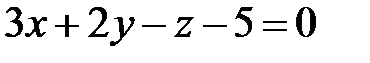6. Скласти рівняння площини, що проходить через пряму 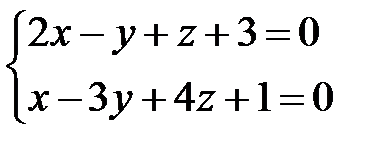паралельно вектору .

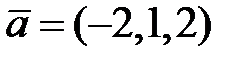7. Перевірити паралельність прямої 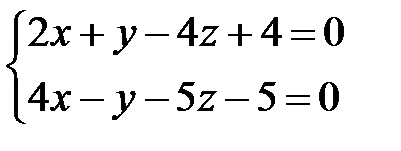та площини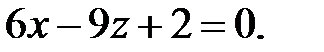

Питання для повторення

1) Кут між прямою і площиною.

2) Умови паралельності та перпендикулярності прямої та площини.

3) Знаходження точки перетину прямої та площини.