Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, тогда эти треугольники подобны.

Комментарий. Вспоминаем первый признак равенства треугольников по двум сторонам и углу между ними. В данном случае, если углы равны, а стороны пропорциональны - то треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны

Свойства подобных треугольников

Площади подобных треугольников соотносятся как квадрат соотношений их подобных сторон.

Простейшие задачи на подобие треугольников

Задача.
Даны подобные треугольники:
1)АВС и KLM
АС = 17 см, АВ = 9 см, ВС = 10 см, ML = 7,5 см, LK = 6,75 см, MK = 12,75 см
2)АВС и МКС
АВ = 4 см, АС = 6см, ВС = 5см, МС = 3 см, СК = 2,5 см, МК = 2 см
Составьте отношение их сходственных сторон.Определите коэффициент подобия.

Решение.
Поскольку треугольники по условию задачи подобны, то для нахождения сходственных сторон выстроим их по возрастанию, так как у подобного треугольника стороны также будут иметь соответствующие размеры, умноженные на коэффициент подобия

1) АВ=9 см; ВС=10 см; АС=17 см; и LK=6,75 см; ML=7,5 см; MK=12,75 см
2) АВ = 4 см; ВС = 5см; АС = 6см; и МК = 2 см; СК = 2,5 см; МС = 3 см

Теперь вычислим соотношение двух наименьших сторон, оно будет точно таким же, как двух наибольших или средних по величине сторон. Это и есть коэффициент подобия данных треугольников.

1) AB / LK = 9 / 6,75 = 1 1/3 Внимание! Переведите десятичные дроби в простые, чтобы получить верный коэффициент подобия. AB/ LK = BC / ML = AC / MK = 1 1/3
2) AB / MK = 4 / 2 = 2, AB / MK = BC / CK = AC / MC = 2

Подобие треугольников. Первый признак подобия

Примечание. Это урок с задачами по геометрии о подобии треугольников. Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.

Задача

В треугольнике ABC угол A вдвое больше угла B, а длины противолежащих этим углам сторон соответственно равны 12 и 8. Найти третью сторону.
Второй признак подобия треугольников - student2.ru

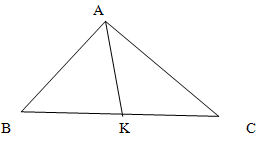
Решение.
Для угла А построим биссектрису на противоположную сторону BC. Пусть она пересечет противоположную сторону в точке К.

Исходя из того, что AK - биссектриса, углы ABC и KAC - равны. Поскольку угол С у них общий, то и третий угол этих треугольников является одинаковым. Таким образом, треугольники являются подобными по трем углам.

Исходя из того, что треугольники ABC и AKC подобны:
AC : BC = KC : AC = AK : AB

AC : BC = KC : AC
8 / 12 = KC / 8
KC = 64 / 12 = 16 / 3

Поскольку угол AKB = ABK (BK - биссектрисса, следовательно - треугольник AKB равнобедренный)
Откуда AK = BK

Учтем, что BK = AC - KC, тогда
AK = BK = 12 - 16 / 3

Теперь вернемся к свойствам подобных треугольников
KC : AC = AK : AB
и подставим известные значения
(16 / 3 ) / 8 = ( 12 - 16 / 3 ) / AB
AB = (AK * AC) / KC = 10

Ответ: 10 см

Подобие треугольников. Третий признак подобия

В этом уроке, вы найдете решение задач по геометрии, которые используют правила подобия треугольников и являются интересными для решения. Я их размещаю здесь если они вызывают некоторые трудности при решении у школьников.

Задача

Треугольники ABC и A₁B₁C₁ подобны. Соотношение сторон теругольников 3:4 . Площадь одного из них больше площади другого на 14 см². Найдите площади треугольников.

Решение

Для решения данной задачи будем руководствоваться основным свойством подобия треугольников - все размеры одного теругольника подобны размерам другого. Сначала опустим на сторону а каждого треугольника высоту h. Таким образом площадь первого треугольника будет выражаться формулой S₁=1/2ah, а площадь второго треугольника формулой S₂=1/2*3/4a*3/4h. Таким образом, можно определить соотношение площадей треугольников:

S₁/S₂ = 1/2 ah / ( 1/2 * 9/16 ah)

S₁/S₂ = ah / ( 9/16 ah)

S₁/S₂ = 16/9

Выше перечисленные преобразования мы могли бы не проводить, если нам известна теорема: "площади подобных треугольников относятся как квадрат соотношения их сторон"

Выразим площадь одного треугольника через площадь другого:

S1=16S₂/9

По условию задачи S₁-S₂=14, таким образом

16S₂/9-S₂=14

7/9S₂=14

S₂=18, следовательно S₁ = 14+18=32

Ответ: 18 и 32

Задача

Стороны AB и DC трапеции ABCD продлили так, что прямые AB и DC пересеклись в точке E. Таким образом, продолжения сторон трапеции образовали треугольник площадью 98 квадратных сантиметров. Найти площадь трапеции, если ее основания относятся друг к другу как 5 к 7.

Решение

Начало решения.

Из условия задачи видно, что у нас получились треугольники EAD и EBC. Поскольку оба треугольника имеют общий угол E, а основания трапеции, являющиеся параллельными, согласно теореме Фалеса, отсекают на сторонах AE и DE пропорциональные отрезки отрезки, то треугольники EAD и EBC являются подобными.

Способ 1.

Опустим из вершины E высоту на основание AD. Она же будет высотой для основания BC, поскольку основания трапеции параллельны. Обозначим высоту для треугольника EAD как h₁, а для треугольника EBC как h₂.

Таким образом:
Площадь треугольника EAD будет равна S_EAD=1/2*AD*h₁.
Площадь треугольника EBC будет равна S_EBC=1/2*BC*h₂.

Поскольку треугольники подобны, то все стороны относятся друг к другу с одним и тем же коэффициентом подобия. Поскольку основания трапеции относятся дрцг к другу как 5:7, то и все остальные стороны относятся друг к другу с тем же соотношением. Из этого следует:
BC / AD = 5 / 7
BC = 5AD / 7

аналогично:
h₂/ h₁= 5 / 7
h₂= 5h₁/ 7

Таким образом:
S_EBC=1/2*BC*h₂.
Подставим значения сторон меньшего подобного треугольника через значения сторон большего подобного треугольника:
S_EBC=1/2*(5AD / 7)*(5h₁/ 7)
S_EBC=1/2*AD*h₁*25 / 49

Заметим, что по условию задачи площадь получившегося треугольника EAD равна 98 сантиметрам, одновременно S_EAD=1/2*AD*h₁.
Подставим вместо указанного выражения его значение:
S_EBC = 98*25/49
S_EBC= 50 см²

Способ 2.

Если нам известна теорема: "площади подобных треугольников относятся как квадрат соотношения их сторон", то площади подобных треугольников AED и BEC будут соотноситься как 5² : 7². То есть:
S_EBC / S_EAD = 5² / 7²
S_EBC / S_EAD = 25 / 49
S_EBC = S_EAD * 25 / 49