Дифференциальные уравнения I порядка

Дифференциальные уравнения

Общие понятия

Определение 1. Обыкновенным дифференциальным уравнением n–ого порядка называется соотношение вида: 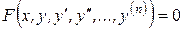(1),

где 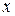– независимая переменная; 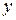– искомая функция переменной;

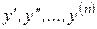– производные искомой функции; 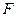– известная функция своих аргументов.

Считается, что производная 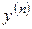на самом деле входит в выражение (1), а величины 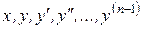могут и не входить в него.

Определение 2. Порядком дифференциального уравнения, n, называется наивысший порядок производной, входящей в это уравнение.

Пример.

1) 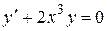– уравнение первого порядка;

2) 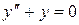– уравнение второго порядка;

3) 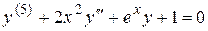– уравнение пятого порядка.

Определение 3. Всякая функция 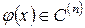, которая, будучи подставленная вместо y в выражение (1), обращает это выражение в тождество, называется решением дифференциального уравнения (1).

Если 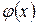– решение, то по определению

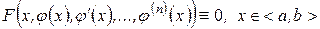(2)

Пример.

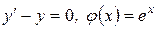– решение, так как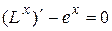

У рассматриваемого уравнения есть еще такое решение: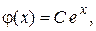

где С – произвольная постоянная.

Это значит, что это уравнение имеет бесчисленное множество решений, зависящих от одного параметра (С).

Можно показать, что уравнение n–ого порядка имеет семейство решений, зависящих от произвольных независимых друг от друга постоянных.

Пример.

Уравнение 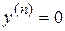имеет решение:

.

Определение 4. Процесс разыскания решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Определение 5. Решение дифференциального уравнения (1), содержащее n независимых между собой произвольных постоянных, называется его общим решением.

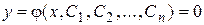, (3)

Замечание. Дифференциальное уравнение может иметь не одно, а несколько общих решений. Например, для уравнения 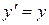функции и 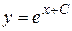являются общими решениями, причем разными, так как первая из них обращается в нуль (С=0), а вторая – никогда в нуль не обращается.

Определение 6. Соотношение 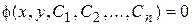, (4)

связывающее между собой независимую переменную, искомую функцию и n произвольных постоянных, называется общим интегралом уравнения (1). Следовательно, в общем интеграле решение задано в неявном виде.

Пример.

Рассмотрим уравнение: 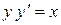. Отсюда 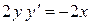или 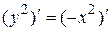. Поэтому 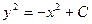, где С – произвольная постоянная.

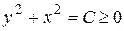– общий интеграл; 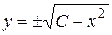– общее решение.

Определение 7. Решение, полученное из общего при фиксированных значениях произвольных постоянных, называется частным решением.

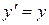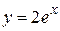Пример. Уравнение . Его общее решение . Положим С=2, тогда – частное решение.

Определение 8. Особым решением по отношению к данному общему решению называется такое решение, которое не может быть получено ни при каких значениях произвольных постоянных, входящих в общее решение.

Пример. Уравнение 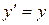имеет два общих решения:

1) 2)

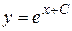
Решение: 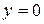есть частное по отношению к первому и особое по отношению ко второму общему решению.

Определение 9. График частного решения называется интегральной кривой рассматриваемого дифференциального уравнения. Уравнение этой линии есть уравнение (3) и (4) при фиксированных .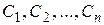

Таким образом, общее решение (или общий интеграл) определяет семейство интегральных кривых, каждая из которых соответствует определенному набору значений 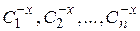произвольных постоянных.

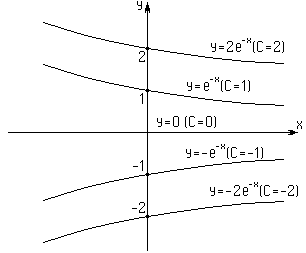Пример. 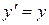. Общее решение .

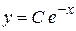Дифференциальные уравнения I порядка

Определение 1. Дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную, искомую функцию и ее производную: 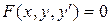(1)

Обычно мы будем иметь дело с уравнениями, которые можно разрешить относительно производной 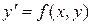(2)

Если в (2) положить 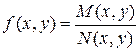, то уравнение (2) можно записать в симметричной форме: 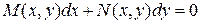(3)

Здесь переменные x и y равноправны.

Иногда бывает выгодно рассматривать х как функцию y. В этом случае часто применяют форму записи (3).

Пример.

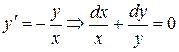
Задача Коши.

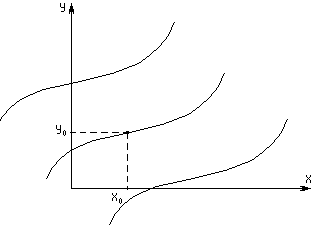
Пусть 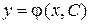будет общим решением уравнения (2). Это общее решение определяет семейство интегральных кривых. Для того чтобы из этого семейства выделить какое-либо частное решение, необходимо задать еще дополнительные условия, в частности, частное решение можно выделить путем задания на плоскости точки 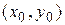, через которую проходит интересующая нас интегральная кривая. Следовательно, возникает задача отыскания такого решения уравнения 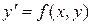, которое при заданном 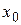принимает заданное значение .

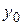Это записывают так: 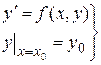(4)

Такая задача называется задачей Коши.

Условие 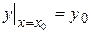называется начальным условием. Начальные условия необходимы для определения соответствующего значения произвольной постоянной С. Покажем на примере как вычисляется С.

Пусть требуется среди решений уравнения 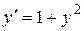(5)

найти такое, которое при 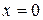обращается в нуль, т.е. 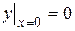. (6)

Общим решением служит функция 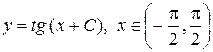(7)

Так как требуется, чтобы выполнялось (6), то должно быть 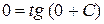, а это возможно только при 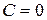. Следовательно, частное решение, удовлетворяющее условию (6), получается из общего решения при 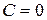, т.е. 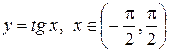. Это и есть решение задачи Коши.

Основное свойство общего решения:

Общее решение 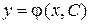дифференциального уравнения 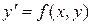обладает тем свойством, что из него по любому заданному допустимому начальному условию 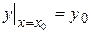может быть найдено частное решение, удовлетворяющее этому условию. Это означает, что подставив в общее решение 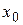вместо 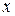и 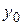вместо 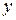, получаем уравнение относительно С: 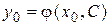, из которого всегда может быть найдено значение 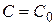и притом единственное. Функция 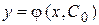служит искомым частным решением.

Замечания:

1. Сформулированное основное свойство общего решения справедливо при определенных требованиях, наложенных на функцию 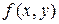. Эти требования даются теоремой существования и единственности.

2. Допустимыми начальными условиями 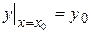называются такие условия, когда точка 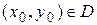, где D – область определения функции .

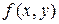3. Пусть 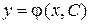будет общим решением некоторого дифференциального уравнения.

Поставим вопрос: можно ли по известному общему решению «восстановить» то дифференциальное уравнение, для которого данное решение является общим?

На этот вопрос отвечает теорема:

Теорема. Для того, чтобы по известному общему решению 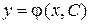восстановить дифференциальное уравнение, нужно исключить С из равенств: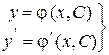

Полученное соотношение 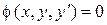и есть то дифференциальное уравнение, для которого 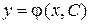служит общим решением. Эту теорему примем без доказательств.

Пример. Пусть дана функция 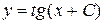, где С – произвольная постоянная. Требуется определить то дифференциальное уравнение, для которого она служит общим решением.

Решение. Используем теорему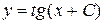

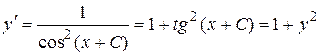
Искомым дифференциальным уравнением будет .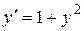

Может случиться, что в равенстве 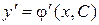исчезнет произвольное постоянное. Это значит, что это равенство и дает искомое дифференциальное уравнение.

Например, пусть дано общее решение 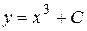. Дифференцируем - 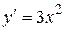. Исчезло С. Следовательно, функция 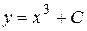служит общим решением уравнения .

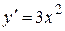Если вместо общего решения задан общий интеграл, то уравнение восстанавливается аналогично.

Именно, надо исключить С из системы: .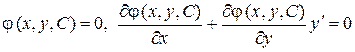

Перейдем к рассмотрению отдельных видов дифференциальных уравнений первого порядка.