Інтерполяційний поліном Лагранжа

ІнтерполЯЦІЯ ФУНКЦІЙ

Постановка задачі

Нехай відомо, що функція y=f(x) існує на інтервалі [a,b]і уn точках цього інтервалу 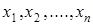вона приймає значення 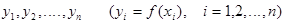.Треба визначити значення функції при аргументі xÎ[a,b],при чому 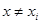i= 1,2 ...,n .

Така задача виникає, наприклад, коли залежність y(x) визначається експериментально при обмеженій кількості вимірювань - n. Додаткові вимірювання з якоїсь причини (дорого, обмежена кількість дослідних зразків тощо) зробити неможливо, але треба оцінити значення y при значеннях x, таких що не використовувались при вимірюваннях. Очевидно такі умови не дозволяють точно визначити y(x) при 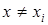. Можна отримати тільки наближену оцінку, виходячи з певного припущення про характер функціональної залежності між y та x . Аналогічна задача виникає при використанні таблиць функцій. Наприклад, треба знайти ln4.63, а у таблиці є тільки ln4.6 і ln4.7. В усіх цих випадках виникає задача інтерполяції - наближеного відновлення функціональної залежності в інтервалах між вузлами x_i.

Для розв’язання цієї задачі використовується інтерполяційна функція Y(x), така що

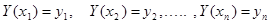(2.1)

Значення функції y(x) знаходяться наближено y(x)» Y(x). На вибір інтерполяційної функції Y(x) впливає характер залежності y(x), але у загальному випадку частіше використовуються степеневі поліноми

(2.2)

Таким чином, для розв’язання задачі інтерполяції треба знайти поліном (2.2), що задоволить умови (2.1).

Метод невизначених коефіцієнтів

Поліном степеня m визначається своїми m+1 коефіцієнтами. Приймемо його у вигляді 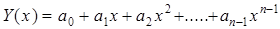і підставимо у (2.1). Отримаємо систему n лінійних алгебраїчних рівнянь з n невідомими 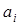i=0,1,...n-1.

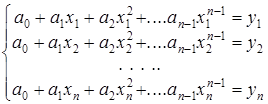
Визначник цієї системи є визначником Вандермонда і, якщо усі x₂ різні, то він не дорівнює 0. У цьому випадку система має єдиний розв’язок, який і визначає поліном, що потрібен. Цей підхід доцільний тільки для того, щоб довести існування і єдиність інтерполяційного поліному, а для його побудови існують явні методи, які будуть розглянуті нижче.

Інтерполяційний поліном Лагранжа

Інтерполяційна формула Лагранжа дозволяє побудувати поліном степеня n-1, що задовольняє умови (2.1), і має наступний вигляд:

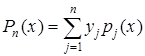, (2.3)

де 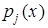- поліном степеня n-1 такий, що:

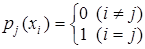, (2.4)

Вираз (2.4) означає, що поліном 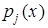має корені 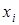при i¹j, і це дає змогу записати його у явному вигляді:

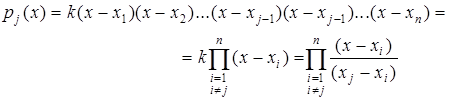(2.5)

У цьому виразі коефіцієнт k обирається таким, щоб .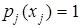

Підставляючи (2.5) у (2.3), отримуємо формулу Лагранжа у зручному для програмування вигляді:

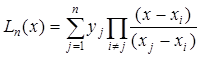. (2.6)

Існують інші форми запису інтерполяційного поліному, які можуть бути більш зручними у конкретних випадках ніж формула Лагранжа. Так інтерполяційна формула Ньютона з розділеними різницями подає інтерполяційний поліном як узагальнення відрізку ряду Тейлора.

Розділені різниці

Поняття розділеної різниці можна розглядати як узагальнення поняття похідної.

Для функції 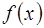розділена різниця нульового порядку 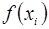співпадає з її значенням.

1^го порядку – визначається формулою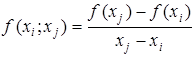

2^го порядку - 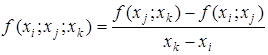(2.7)

k^го порядку -

Інтерполяційний поліном НЬЮТОНА

Різниця між деякою функцією 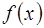та її інтерполяційним поліномом у формі Лагранжа може бути подана у наступному вигляді.

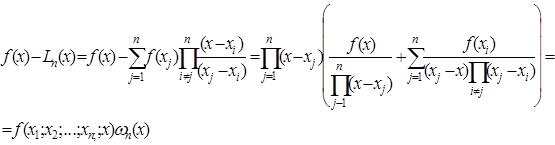(2.8)

де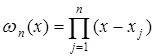

Використовуючи це, різницю між інтерполяційними поліномами, побудованими відповідно по m та m-1 вузлах можна подати таким чином:

.

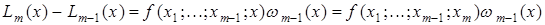Звідси поліном, що будується по довільній кількості вузлів n може бути записаний у наступній формі

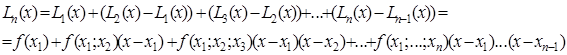, (2.9)

яка зветься інтерполяційною формулою Ньютона з розділеними різницями. Ця формула дозволяє зручно включати додаткові вузли інтерполяції, дописуючи відповідні додаткові члени.

Схема Ейткена

Ця схема дозволяє спростити обчислення значень інтерполяційного поліному.

Нехай 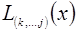- інтерполяційний поліном з вузлами інтерполяції 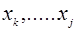Можна перевірити справедливість наступного виразу:

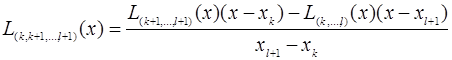(2.10)

Ця формула використовується для послідовного обчислення значень поліномів за наступною схемою:

L₍₁₎(x) L₍₂₎ (x) L₍₃₎(x)_{.....................}L_(n)(x)

L_(1,2)(x) L_(2,3) (x) ..................

L_(1,2,3) (x) .....................

....................

L_(1,2,3,...n) (x)