Что значит найти асимптоты графика функции?
Задание2 : Правило Лопиталя


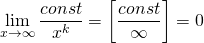
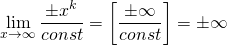
Задание 3 :
Исследование графика функции. Теория.
1. ОДЗ
2. Четность, нечетность. Периодичность
3. Асимптоты
4. Экстремумы функции и интервалы монотонности функции.
5. Интервалы выпуклости функции. Точки перегиба.
6. Промежутки знакопостоянства. Точки пересечения с осями.
7. Построение графика
1) ОДЗ(приведены области допустимых значений): 

2)


3)
Сколько асимптот может быть у графика функции?
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает
Вертикальные асимптоты.Прямая x = aявляется вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:
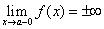 или
или 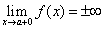 .
.
(при этом функция f(x) может быть вообще не определена соответственно при 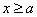 и
и 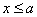 ).
).
Замечание. Символом
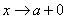
обозначается стремление x к a справа, причём x остаётся больше a, символом
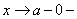
стремление x к a слева, причём x остаётся меньше a.
Из сказанного следует, что вертикальные асимптоты кривой нужно искать в точках разрыва и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.
Пример 1.График функции y = ln x имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе области определения, так как
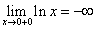
(рис. слева).
Горизонтальные асимптоты.Если
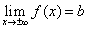
то y = b – горизонтальная асимптота кривой y = f(x) (правая при 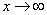 , левая при
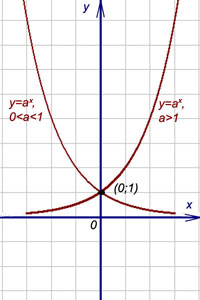
, левая при  и двусторонняя, если пределы при
и двусторонняя, если пределы при 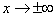 равны).
равны).
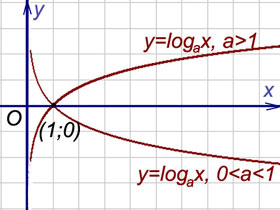
Пример 2.График функции
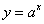
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осьюOx), так как
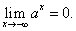
Правой горизонтальной асимптоты у кривой нет, поскольку
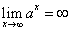
Наклонные асимптоты.Существование наклонной асимптоты определяется следующей теоремой.
Теорема.Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы
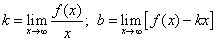 (1)
(1)
или
 (2)
(2)
В первом случае получается правая наклонная асимптота, во втором – левая. Правая наклонная асимптота изображена на рис. снизу.
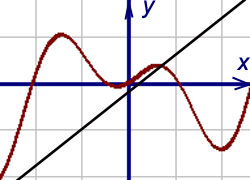
При совпадении пределов (1) и (2) прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
4)
Алгоритм исследования непрерывной функции y=f(x) на монотонность и экстремумы:
1. Найти производную f'(x).
2. Найти стационарные и критические точки.
3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4. Опираясь на теоремы 1, 2 и 4, сделать выводы о монотонности функции и о ее точках экстремума.
